1. 선형결합
1) 선형결합 (Linear Combination)
선형 결합 (혹은 일차 결합)은 각 항에 상수를 곱하고 결과를 더함으로써 일련의 항으로 구성된 표현식입니다.

이런 식으로 말이죠.
이전 글 '[수학] 벡터'에서 벡터와 스칼라곱의 연산을 다룬적이 있습니다.
임의의 벡터 V를 체 K 위에 정의한다고 하면,
벡터 V의 원소를 v1, v2, v3 ...
스칼라를 a1, a2, a3 ... 로 나타낼 수 있는데,
스칼라 계수와 벡터의 선형결합을 이용해서 새로운 벡터를 만들어 낼 수 있습니다.

이런 식으로 말이죠.
이를 벡터의 선형생성이라고 부릅니다.
수학에서는 span 이라고 표현합니다.
2) 선형독립

실수 n차원 공간에서 정의된 임의의 벡터 V에 대해서
벡터의 방정식이 자명해를 갖고 있을 시에 선형독립이라고 부릅니다.
3) 선형의존

그러나 c1, c2, ... , cp 중 하나라도 0이아닌 계수를 가지고 있으면 선형 종속이라고 합니다.
4) 선형독립 vs 선형의존

v1, v2, v3가 선형 독립관계인지 선형 의존관계인지 평가해보도록 하겠습니다.

a1 = -2, a2 = 1. a3 = -1
을 대입할 시 0벡터를 만족합니다.
즉, 0이 아닌 계수를 가지면서 0벡터를 만들 수 있기 때문에
위 벡터는 선형의존에 있다고 할 수 있습니다.
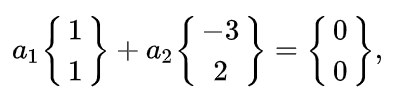
이 식을 한 번 봅시다.

이 행렬을 연산하면 이렇게 되는데,
어떤 계수가 0이 되어야만 식이 영 벡터를 만들 수 있으므로 이는
선형 독립입니다.
어떤 벡터들이 선형관계에 있는지, 종속관계에 있는지 쉽게확인하는 방법은 다음과 같습니다.
1) 벡터의 개수 > 벡터의 차원 수
2) 어떤 벡터로 다른 벡터를 선형 조합할 수 있는 경우
3) 값이 같은 벡터가 있을 경우
4) 선형 조합 식에서 0 벡터를 만들 수 있는 어떤 스칼라 값이 0일 경우
는 모두 선형 종속입니다.
5) 선형생성
선형 결합을 통해서 다른 벡터를 만들 수 있습니다.
이를 선형생성이라고 합니다.
선형 독립상태의 어떤 벡터를 선형 결합하면 해당 차원의 모든 벡터를 만들 수 있습니다.
그러나, 선형 종속관계의 어떤 벡터를 선형 결합 할 시, 어떤 식으로 선형 결합하든 하나의 벡터만 만들 수 있습니다.
벡터 (1,2) 와 벡터 (2,4) 의 경우 종속관계에 있습니다.
그러므로 벡터 (1, 2)의 스칼라 곱으로만 표현되는 벡터만 생성할 수 있습니다.
그러나
벡터 (2, 1) 백터 (1, 3) 의 경우 독립관계에 있으므로
2차원 평면위에 있는 모든 벡터를 선형 결합을 통해 만들 수 있습니다.
2. 기저(Basis)와 차원(Dimension)
1. 기저
어떤 벡터 공간의 기저란, 그 벡터 공간을 선형생성하는 선형독립인 벡터들을 뜻합니다.
기저는 집합의 개념이고, 기저의 요소들은 모두 선형독립인 벡터들입니다..
이러한 기저의 요소 벡터를 기저벡터 Basis라고 부르며,
기저 벡터의 선형생성을 통해 해당 차원의 모든 벡터를 만들어낼 수 있습니다.
2. 차원
어떤 기저가 가지는 원소의 수를 차원이라고 부릅니다.
즉, 2차원 이라는 것은 어떤 기저가 가지는 원소의 수가 2개라는 것을 뜻합니다.
2차원 공간에서 어떤 다른 벡터들이 기저를 형성하기 위해서는
- 벡터들이 서로 선형 독립이어야 하고
- 벡터들이 2개여야 합니다.
2차원 공간에서 벡터들이 3개일 경우 선형 독립을 형성할 수 없기에 기저 집합의 조건을 만족할 수 없습니다.
3. 표준 기저 벡터
일반적으로 n차 단위행렬의 열벡터 e1, e2 ... en은 R^n의 기저벡터입니다.
즉, 유클리드 공간 R^3 에서는
e1 = (1,0,0)
e2 = (0,1,0)
e3 = (0,0,1)
이 기저벡터인데요.
이를 표준 기저 벡터라고 합니다.
벡터 공간의 기저는 유일하지 않으며,
단위행렬의 열벡터로 정의되는 기저 벡터를 표준 기저 벡터라 하고,
이러한 기저를 표준 기저라고 합니다.
'컴퓨터 그래픽스 > 수학' 카테고리의 다른 글
| [수학] 벡터: 가상 공간의 탄생 (0) | 2024.06.27 |
|---|---|
| [수학] 수: 가상 세계를 구성하는 가장 작은 단위 (0) | 2024.06.27 |
| [수학] 삼각함수 (0) | 2024.02.03 |
| [수학] 벡터 (1) | 2024.02.01 |
| [수학] 함수에 대해서 (1) | 2024.01.31 |