1. 벡터의 정의
1) 데카르트 좌표계 (Cartesian Coordinate System)

데카르트 좌표계란 임의의 차원의 유클리드 공간을 나타내는 좌표계 중 하나입니다.
유클리드 공간은 평면과 공간을 일반화한 것으로 유클리드가 생각했던 거리, 길이, 각도를 좌표계에 도입하여, 임의 차원 공간으로 확장한 것입니다.
유클리드 공간은 유한 차원, 실수, 내적 공간으로 n차원 유클리드 공간은 실수 집합 R의 n번 곱집합이죠.
간단하게 말해서
2차원 데카르트 좌표계는 2차원 유클리드 공간에서의 좌표 평면
3차원 데카르트 좌표계는 3차원 유클리드 공간에서의 좌표 공간
이라고 할 수 있겠습니다.

이 2차원 데카르트 좌표계는
2개의 실수 집합 R을 곱집합한 원소들의 집합, RxR 로 표현할 수 있고
흔히 가로축을 x축, 세로축을 y축 이라고 합니다.
그래서 이를 좌표(Coordinate)라고 하죠.
그리고 이 곱집합의 원소를 표현할 때, 튜플을 이용해서 (x, y)라고 표현합니다.
각 축의 집합은 독립적입니다.
각 축이 90도로 직교한다는 것은 각각이 독립적이라는 것을 뜻하기도 합니다.
2) 벡터 공간
벡터 공간이란 체(Field) F에 대한 가군(module) (V, +, ㆍ) 을 벡터공간이라하고
V의 원소를 벡터라고 합니다.
이때, +는 벡터의 덧셈이고, ㆍ는 벡터의 스칼라배입니다.
이 때 스칼라란 벡터 공간을 정의할 때의 체 집합의 원소를 뜻합니다.
간단하게 말해서, 벡터는 2개의 체 집합의 곱집합이라고 말할 수 있습니다.
벡터는 체 집합의 곱집합 형태, 스칼라의 순서쌍, 튜플로 표현할 수 있구요.
2. 벡터의 연산
1) 벡터와 벡터의 덧셈
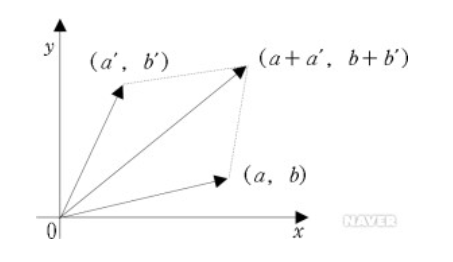
벡터의 덧셈은 벡터와 벡터 관계에서만 정의됩니다.
벡터끼리의 덧셈은 각 성분을 더해주는 것으로 간단하게 정의할 수 있습니다.
2) 벡터와 스칼라의 곱셈

스칼라는 체집합의 원소입니다. 벡터와는 독립적인 수치죠.
임의의 스칼라 값을 k, 임의의 2차원 벡터를 V = (x,y) 라고 할 때,
벡터와 스칼라곱은
kV = (kx, ky) 로 표현되며, 교환법칙이 성립합니다.
3) 벡터의 크기
벡터의 크기는 원점으로 부터의 최단 거리를 뜻하며,

로 표현할 수 있습니다.
임의의 벡터 V의 크기는 ||V|| 로 표현하며, 벡터의 크기 혹은 노름(Norm)이라고 표현합니다.
2차원 벡터의 크기는 x, y에 대한 피타고라스 정의로 구할 수 있죠.
+) 단위 벡터?
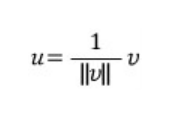
단위 벡터는 크기가 1인 벡터를 뜻합니다.
임의의 벡터 V가 있을 때,
||V||의 역수와 벡터 V의 스칼라곱의 결과는 단위 벡터입니다.
4) 추후에 다룰 연산
백터의 내적과 외적
3. 벡터 공간의 공리
벡터 공간은 체를 기반으로 확장해 만든 시스템으로 볼 수 있으며, 이는 8개의 공리고 구성되어 있습니다.
참고: u, v, w 는 벡터, a, b 는 스칼라를 의미합니다.
(1) 덧셈 연산의 결합법칙
u + ( v + w) = (u + v) + w
(2) 덧셈 연산의 교환법치
u + v = v + u
(3) 덧셈 연산의 항등원
v + 0 = v (0은 영벡터를 의미)
(4) 덧셈 연산의 역원
v + (-v) = 0
(5) 스칼라 곱의 호환성
a(bv) = (ab)v
(6) 스칼라 곱셈 연산의 항등원
1v = v
(7) 벡터 덧셈과 스칼라 곱셉의 분배법칙
a(u + v) = au + av
(8) 스칼라 덧셈과 스칼라 곱셈의 분배법칙
(a + b)v = av + bv
(벡터와 스칼라 곱셈 연산의 역원은 존재하기 때문에 벡터 공간에서의 나눗셈 연산은 정의하지 못합니다.)
만일 벡터 공간의 기반을 이루는 체 집합을 실수 집합 R을 사용하는 경우
이를 실수 벡터 공간이라고 합니다.
'컴퓨터 그래픽스 > 수학' 카테고리의 다른 글
| [수학] 벡터: 가상 공간의 탄생 (0) | 2024.06.27 |
|---|---|
| [수학] 수: 가상 세계를 구성하는 가장 작은 단위 (0) | 2024.06.27 |
| [수학] 삼각함수 (0) | 2024.02.03 |
| [수학] 선형결합, 기저와 차원 (0) | 2024.02.03 |
| [수학] 함수에 대해서 (1) | 2024.01.31 |