개발하는 리프터 꽃게맨입니다.
[수학] 삼각함수 본문
삼각함수 개요 (Trigonometric Function)
삼각함수는 각의 크기를 삼각비로 나타내는 함수를 합니다.
즉, 삼각형의 각도와 변의 길이의 관계를 다루는 함수라고 생각할 수 있죠.
1. 직각삼각형의 3요소

직각삼각형에는 3개의 요소가 있는데요.
빗변 (hypotenuse)
밑변 (adjacent)
높이 (opposite)
가 있습니다.
2. 삼각비
삼각비란 직각삼각형의 3변 중 2 변의 길이간의 비례 관계를 나타내는 값입니다.

3. 삼각함수
삼각비의 의미를 함수의 개념으로 확장시킨 것을 삼각함수라고 볼 수 있습니다.
여러가지 정의법이 있을 수 있지만, 저는 단위원으로 정의해보겠습니다.

좌표 평면 상에서 원점 O를 중심으로하는 단위원을 고려할 때,
단위원의 한 점 P(x,y) 라하고
원점 O와 점 P를 잇는 직선와 양의 x축간의 각의 크기를 세타라 할 때, 삼각함수를 다음과 같이 정의합니다.

만약 단위원이 아니라 반지름이 r인 원 위의 점 (x, y)에 대해서 정의한다면
그 정의는 다음과 같습니다.
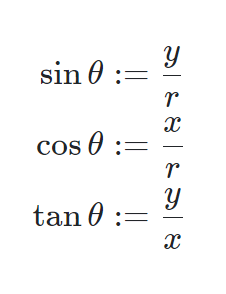
이 때,
sin, cos 의 정의역은 실수, 치역은 [-1, 1] 입니다.
4. 삼각함수의 그래프
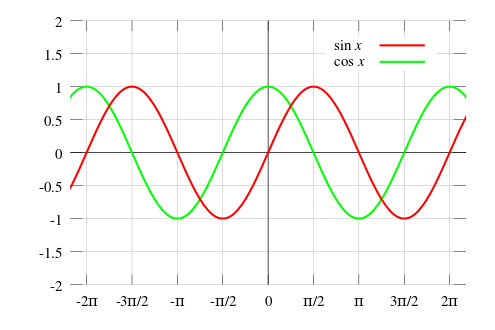
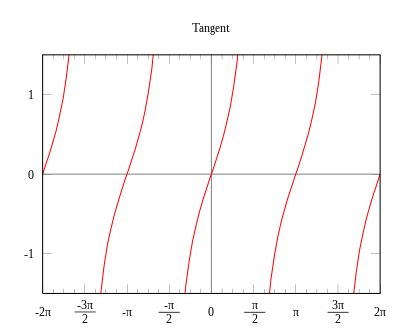
5. 코사인과 사인 함수의 성질
1) 사인 함수와 코사인 함수는 항상 [-1, 1] 범위를 일정하게 반복되는 패턴을 가진다.
2) 사인과 코사인 함수는 2pi (360도) 단위로 반복된다.
3) 사인 함수는 기함수, 코사인 함수는 우함수다.
4) 피타고라스의 정리에 의해 아래 식은 항상 성립한다.
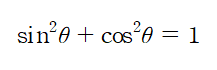
6. 탄젠트 함수의 성질
1) 분모가 0인 경우는 정의되지 않으므로, 밑변이 0인 경우는 탄젠트를 정의할 수 없다.
즉, 탄젠트의 세타 값이 ((1/2)세타 + 2n세타) 인 경우 탄젠트를 정의할 수 없다.
7. 특수각
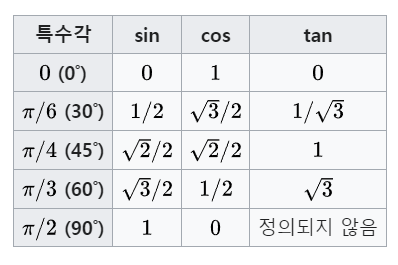
8. 삼각함수의 덧셈정리
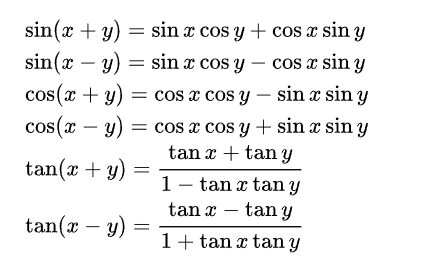
9. 삼각함수의 미분과 적분
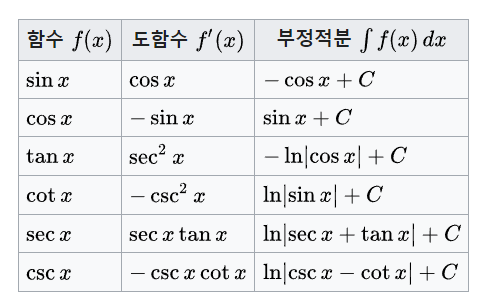
각의 측정
1. 육십분법 (Degree)
한 바퀴를 360도로 나누어 표현하는 것을 60분법이라고 부릅니다.
2. 호도법 (Radian)
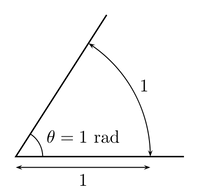
호의 길이로 각도를 나타내는 방법으로, 원의 둘레는 반지름의 2pi 배로 항상일정하며
부채꼴에서 호의 길이는 중심각에 비례한다는 기본 원리를 이용해서 정의된 각 측정법입니다.
어느 한 원 위의 점이 원점을 중심으로 반지름의 길이만큼 한 방향으로 움직였을 때 대응하는 각의 크기를
1 rad (라디안) 이라고 부릅니다.
즉, 반지름이 r인 원에 대해서
한 점이 r만큼 움직였으면 1 rad
한 점이 지름인 2*pi*r 만큼 움직였으면 2*pi rad 입니다.
즉, 360도는 2*pi rad 와 대응됩니다.
그러므로
1 rad 는 대략 57.3도 입니다.
아래는 60분법과 라디안의 관계입니다.
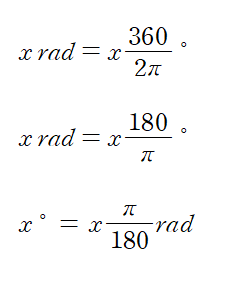
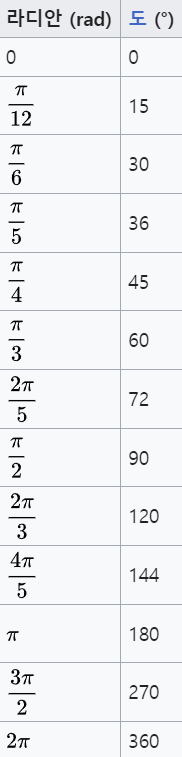
호도법을 다루는 이유는
컴퓨터에서 사용하는 삼각함수의 매개변수로 전부 라디안각이 사용되기 때문입니다.
벡터의 회전변환
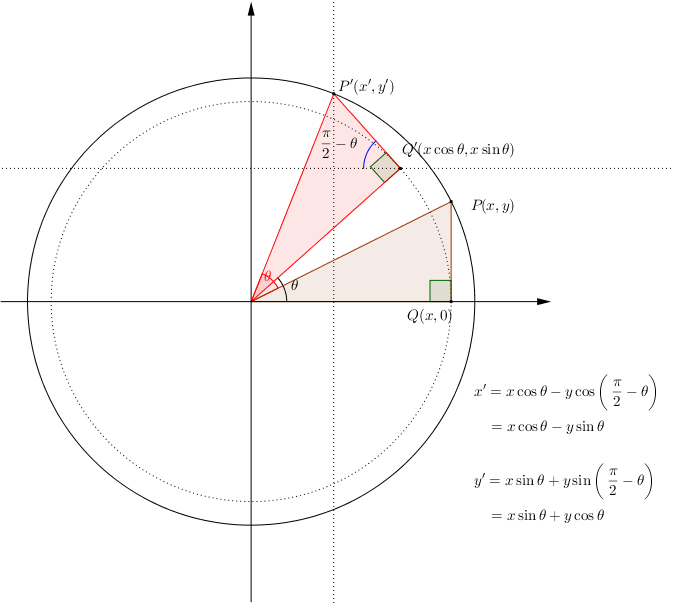
임의의 2차원 벡터 v = (x, y) 가 있다고 해봅시다.
이걸을 세타만큼 회전시키면 v`의 좌표는 어떻게 될까요?
2차원 백터는 표준 기저 벡터의 선형결합을 통해 만들 수 있습니다.
(x, y) = x(1,0) + y(0,1)
이 때 새로운 두 기저 벡터가 크기가 1, 직교하는 상태와 현재 방향을 유지하면서 변형하는 것을 회전 변환이라고 하며
각 세타만큼 발생한 회전 변환을 통해 생기는 벡터는 다음과 같습니다.
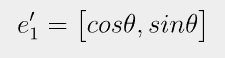
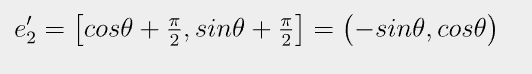
이제 이 것을 기저벡터로 하여 선형 결합을 통해 세타만큼 회전 변환을 수행한 벡터를 만들 수 있습니다.
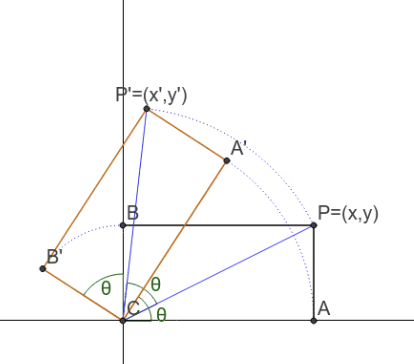
그래서 P(x, y)는 회전 변환시
P(xcos - ysin, xsin + ycos)) 로 변환할 수 있습니다.
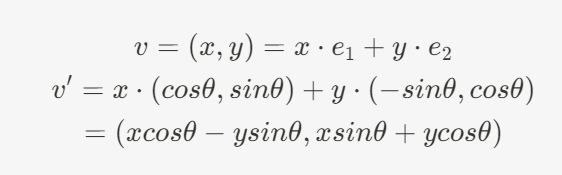
삼각함수와 역함수
역함수가 존재하기 위해서는 전단사함수여야 합니다.
그러나 삼각함수는 일대일대응하는 함수가 아니기 때문에 (단사함수가 아니기 때문에)
역함수가 존재하지 않습니다.
하지만 제한된 범위에서는 전단사함수를 만족하기 때문에,
정의역을 제한하여 역함수를 정의할 수 있다.
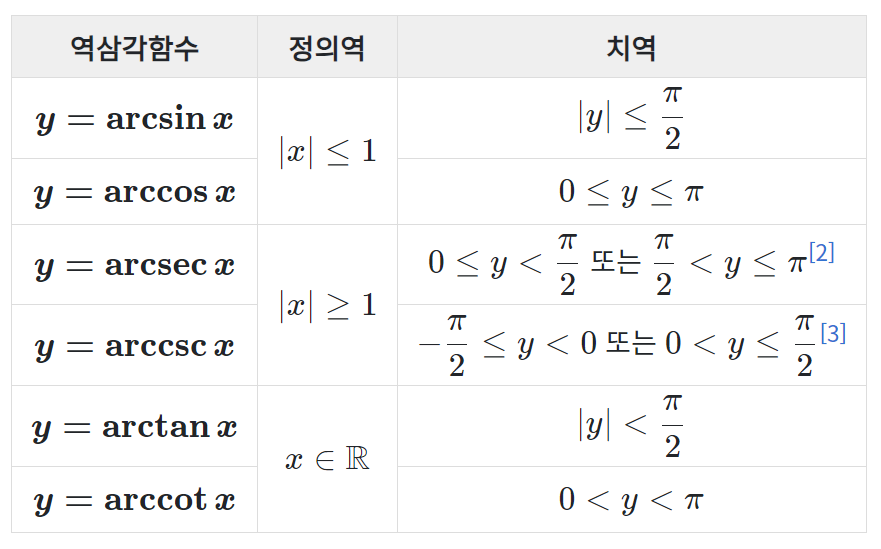
즉,
사인 함수는 [- pi/2 , pi/2]
코사인 함수는 [0, pi]
탄젠트 함수는 (-pi/2, pi/2)
의 정의역에서 역함수를 정의할 수 있습니다.
2) 역삼각함수의 그래프
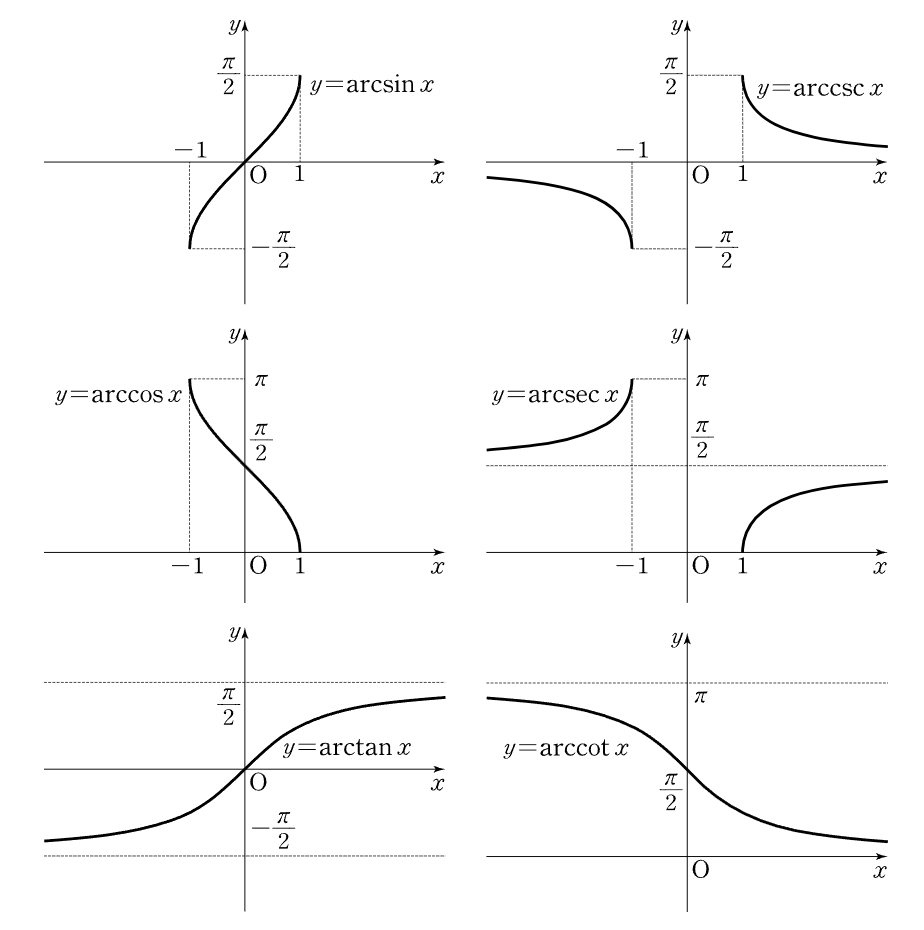
3) 역삼각함수의 한계점
역삼각함수는 삼각비를 이용해서 역으로 각도를 얻어올 수 있기에 매우 유용한 함수입니다.
그러나 한계점이 있습니다.
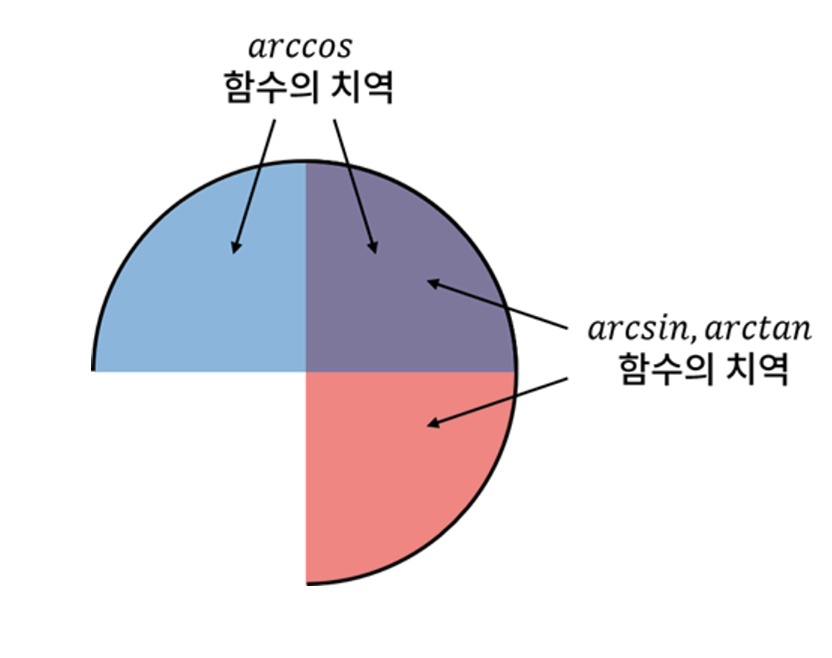
바로 pi ~ 3/2pi 부분의 각도는 구할 수 없다는 것이죠.
그래서 이 경우에는 아크탄젠트 함수의 특징을 활용해서 각도를 구하게 됩니다.
1사분면에 있던 3사분면에 있던 아크탄젠트값은 동일합니다.
그러나 3사분면의 경우 아크탄젠트의 치역에 포함되지 않기 때문에 각도를 구할 수 없죠.
그래서 컴퓨터 프로그래밍에서 탄젠트 값을 이용해서 각도를 구할 때는
앞서 말한 문제점을 보정해주는 atan2 함수가 제공됩니다.
기존 atan의 경우 tan의 함수값을 받아 각도를 리턴하지만
atan2는 좌표를 받아 부호를 판단하여 적절한 함수값을 리턴합니다.
극 좌표계
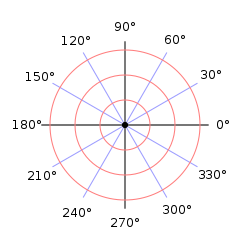
극좌표계는 편병 위의 위치는 각도와 거리를 써서 나타내는 2차원 좌표계입니다.
두 점 사이의 관계가 각이나 거리로 쉽게 표현되는 경우에 가장 유용하죠.
데카르트 좌표계에서는 삼각함수로 복잡하게 나타나는 관계가 극좌표계에서는 간단하게 표현됩니다.
(x, y) 로 표현되는 데카르트 좌표계와는 달리
(r, 세타) 로 표현됩니다.
데카르트 좌표계와 극좌표계의 변환은 다음과 같습니다.
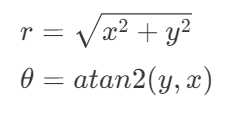
'컴퓨터 그래픽스 > 수학' 카테고리의 다른 글
| [수학] 벡터: 가상 공간의 탄생 (0) | 2024.06.27 |
|---|---|
| [수학] 수: 가상 세계를 구성하는 가장 작은 단위 (0) | 2024.06.27 |
| [수학] 선형결합, 기저와 차원 (0) | 2024.02.03 |
| [수학] 벡터 (1) | 2024.02.01 |
| [수학] 함수에 대해서 (1) | 2024.01.31 |





