개발하는 리프터 꽃게맨입니다.
[C++/자료구조] 선형조사법과 체이닝 해쉬 본문
https://powerclabman.tistory.com/58 (이전 글)
충돌 이슈
1) 개요
해쉬에서 충돌은 불가피합니다.
어떤 키값이 들어올지 예측하지 못하기 때문에
그리고 쓸데없는 메모리 공간을 차지하는 것을 막이 위해
해쉬 테이블은 제한된 공간을 가지고 있고
해쉬 주소는 해쉬 함수를 통해 만들어지는데
다른 키 값에 대해서 값은 해쉬 주소가 나오는 건 어쩔 수 없습니다.
해쉬 테이블의 크기가 M개가 존재한다고 했을때, 들어올 수 있는 데이터의 수는 M 이상 일 수 있기 때문에
충돌이 발생할 수 밖에 없는 것이죠.

사이즈 100의 해쉬 테이블에 30개의 데이터만 넣어도 돌 확률이 99%에 도달합니다.
그래서 기본적으로 충돌이 발생한다고 생각하고,
어떻게 충돌에 대처할 것 인가를 생각하는 것이 중요하죠.
오늘 다룰 주제는 해쉬의 구조입니다.
이번 포스팅에서 선형조사법, 체이닝해쉬
다음 포스팅에서 이차조사법, 이 해쉬
를 차례대로 다루도록 하겠습니다.
선형조사법
1) 개요
충돌 해결법 중 하나인 선형조사법입니다.
추가적인 공간을 사용하지 않고 할당된 메모리 안에서 충돌을 해결합니다.
그래서 Closed hashing, Open addresing이라고 부릅니다.
참고로 다음에 말할 체이닝 해쉬는 정말 반대되는 해결법을 사용합니다.
2) 충돌을 해결하는 방법

충돌을 해결하는 방법은 매우 단순합니다.
충돌을 할 시
해쉬주소 + 1을 해주는 것이죠.
그렇게 빈자리를 찾아가는 것입니다.
그래서 선형탐사법은 충돌이 매우 잦게 발생합니다.
3) 삽입
위 2)에서 설명한 것이 삽입의 로직입니다.
간단히 코드 및 예시만 소개하겠습니다.

참고로 해쉬함수는 어떤 함수를 사용해도 상관없습니다.

저는 간단한거 만들어서 사용했습니다.
4) 탐색
선형탐사법은 충돌이 발생하면 다른 슬롯으로 이동한 다음에 삽입을 하기 때문에
충돌이 발생한 요소를 찾으려면 O(1) 만에 탐색이 불가능합니다.
해쉬 함수를 통해 해쉬 주소를 얻어내서 해쉬 테이블에 접근한 뒤
해쉬 주소 + 1.. 을 반복하면서 내가 삽입한 자료를 찾아야 하는 것이죠.
만약 빈 슬롯을 발견하거나, 해쉬 테이블 전체를 한 바퀴 돌았다면 탐색에 실패한 것입니다.

만약, 탐색에 실패할 시 해쉬주소를 +1 씩 늘려가고
EMPTY 슬롯을 만나거나, 처음주소와 같아지면 탐색을 실패한 것으로 간주합니다.
5) 삭제
선형탐사법에서는 탐사에 있어서 한가지 문제점이 존재합니다.

만약 24를 삭제한다고 했을 때
해쉬함수 값은 3일 것이고, 탐색의 과정을 통해 삭제해서 빈 공간이 생겼다고 가정해봅시다.
그러면, 34는 탐색이 불가능해집니다.
34 또한 해쉬 주소는 3이고, 34를 탐색하기 위해서 3번 인덱스로 접근하여 탐색한다면,
3번 다음 슬롯이 빈공간이라 데이터가 없다고 판단하기 때문이죠.
이럴땐 어떻게 해야 할까요?
바로 Rehashing 입니다.
해쉬테이블에 있는 모든 값이 다 꺼내서, 다시 해쉬 테이블에 삽입하는 연산을 하는 것이죠.
매우 비효율적인 연산같지 않나요..?
그래서 선형탐사법에서는 삭제를 사용하지 않습니다.
삭제를 하려면 rehashing을 해야하는데, 시간적인 소모가 매우 큰 연산이기 때문이죠.
6) Loading factor
선형 탐사법의 경우, 충돌이 많이 발생할수록 탐색, 삽입 등에 있어 매우 성능이 떨어집니다.
심하게는 O(N)의 복잡도가 발생할 수도 있죠.
해쉬를 사용할 때 생각해야 할 것이 바로 Loading factor입니다.
Loadign factor(적재율)은
(요소수)/(테이블크기)
로 나타냅니다.
사이즈 20짜리 테이블에 7개의 요소가 있다면 Loading factor는 0.35 정도 되는 것이죠.
삽입과 탐색에 있어서 해쉬 기법의 이점을 보기 위해서는 항상
Loading factor를 0.5 이하로 유지해줘야만 합니다.
아니면 해쉬를 쓰는 의미가 무색하게 많은 시간이 소요될 수 있기 때문이죠.
Loading Factor는 λ 기호로 표시하는데,
탐색시 탐색을 성공에 있어서 시간복잡도는

이것과 같고
탐색 실패에 있어서 시간복잡도는

위 식과 같습니다.
7) 문제점
(1) 공간의 낭비가 심하다.
loading factor를 0.5 이하로 유지해줘야 한다는 규칙 때문에, 공간복잡도가 매우 커집니다.
10개의 자료를 저장한다고 가정했을 때, 20개 이상의 공간을 할당해야 하기 때문이죠.
(2) 데이터가 몰리는 경향이 있다.
충돌이 발생할 시 충돌발생지역 주변에서 빈 공간을 찾는 로직도 문제가 있습니다.
그러면 해쉬테이블 전체에 데이터가 고르게 분포되어 있는 것이 아니라, 한쪽에 몰리게 되겠죠?
이렇게 특정 영역에 원소가 몰리는 현상을 Primary clustering 이라고 합니다.
이는 해쉬의 효율적인 탐색을 방해합니다.
(3) 요소를 삭제하기 까다롭다.
요소를 삭제하는 것이 어렵다기 보다는 부담스러운 것이죠.
만약 3개의 충돌된 요소 중 가운데 요소를 삭제한다면, 3번째 요소를 찾을 방법은 없습니다.
그래서 보통 삭제를 지원한다면 rehashing을 통해 해시 테이블을 재구성합니다.
그런데 이는 연산 오버헤드가 무겁기 때문에, 보통 선형 탐사법에서는 삭제를 제공하지 않습니다.
7) 전체코드
#include <iostream>
#include <cassert>
using namespace std;
template <typename Ty>
struct BasicHashFunc
{
size_t operator()(Ty item) const
{
return item;
}
};
template <typename Ty, size_t N, typename HashFunction = BasicHashFunc<Ty>>
class LinearProving
{
enum {EMPTY = -1};
public:
LinearProving() { for (auto& it : _items) it = EMPTY; }
~LinearProving() = default;
void Insert(Ty item)
{
assert(_size <= _capacity);
int hashAddr = hashfunc(item) % N;
while (_items[hashAddr] != EMPTY)
hashAddr = (hashAddr + 1) % N;
_items[hashAddr] = item;
_size++;
}
void Search(Ty key) const
{
int firstAddr = hashfunc(key) % N;
int hashAddr = firstAddr;
while (_items[hashAddr] != EMPTY)
{
if (_items[hashAddr] == key) /* 탐색 성공 */
{
cout << "[" << hashAddr << "] : " << key << endl;
return;
}
hashAddr = (hashAddr + 1) % N;
if (_items[hashAddr] == EMPTY || hashAddr == firstAddr) /* 탐색 실패 */
{
cout << "Do Not Exist." << endl;
return;
}
}
}
size_t GetLoadingFactor() const { return _size / _capacity; }
size_t GetSize() const { return _size; }
size_t GetCapacity() const { return _capacity; }
private:
Ty _items[N];
size_t _size = 0;
const size_t _capacity = N;
HashFunction hashfunc;
};
int main() {
srand(time(NULL));
LinearProving<int, 27> h;
h.Insert(rand() % 100);
h.Insert(rand() % 100);
h.Insert(rand() % 100);
h.Insert(rand() % 100);
h.Insert(rand() % 100);
h.Insert(rand() % 100);
h.Search(41);
h.Search(79);
h.Search(24);
return 0;
}
다음 포스팅에서는 선형 탐사법의 Primary clustering 을 해결하기 위한
이차조사법에 대해서 설명하도록 하겠습니다.
체이닝 해쉬
1) 개요
체이닝 해쉬는 해쉬테이블의 요소를 연결리스트로 두어, 충돌이 발생할 시 다른 공간으로 옮기는 것이 아니라, 노드를 추가하는 방식으로 동작합니다.
주어진 데이터 공간 이외로 추가적인 공간을 사용하기 때문에
Open hashing, Separate Chaining 이라고 부릅니다.
2) 충돌을 해결하는 방법

충돌을 해결하는 방법은 다음과 같습니다.
HashTable의 요소를 연결리스트의 헤더로 접근할 수 있도록 구성하고,
item이 들어오면, 헤더에 노드 형태로 만들어서 연결하는 방법입니다.

이때, 연결 리스트의 head를 저장하는 부분을 버켓
버켓을 head로 해서 추가적으로 메모리를 할당해서 chaining 된 노드들을 슬롯
이라고 부릅니다.
3) 구현

C++에서 기본적으로 이중 연결리스트 STL을 제공하기 때문에
STL을 이용해서 만들었습니다.
4) 삽입

선형조사법에 비해서 로직이 매우 간단합니다.
5) 탐색

탐색도 해당 버켓에 접근해서 버켓의 연결리스트를 선형탐색하면 됩니다.
체이닝해쉬의 탐색 시간복잡도 역시 Loading factor로 계산할 수 있습니다.
다시 말하지만 Loading factor 은 (요소 수)/(테이블크기) 입니다.
평균 탐색 성공 시간 복잡도는
1 + 람다/2
평균 탐색 실패 시간 복잡도는
1 + 람다
가 되겠습니다.
6) 삭제
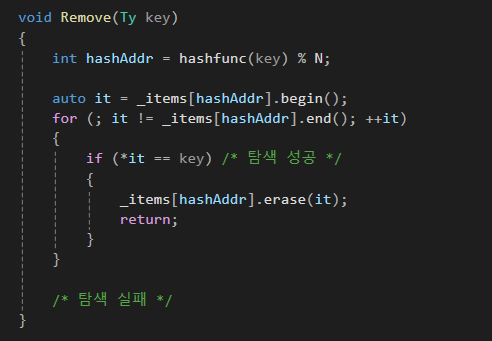
연결리스트는 삭제가 쉽기 때문에, 손쉽게 삭제함수를 구현할 수 있습니다.
7) 문제점
(1) 잦은 충돌시 시간복잡도 증가
체이닝의 탐색, 삭제시 O(1) 만에 버켓에 접근하여 탐색하는 시간은 O(N)만큼 소모됩니다.
그렇기 때문에 한 버켓에 슬롯이 많이 추가될 수록 성능이 떨어질 수 밖에 없습니다.
이를 해결하기 위해서는 버켓의 수를 늘리거나, 좋은 해쉬함수를 사용하는 것이 권장됩니다.
8) 전체 코드
#include <iostream>
#include <list>
#include <cassert>
using namespace std;
template <typename Ty>
struct BasicHashFunc
{
size_t operator()(Ty item) const
{
return item;
}
};
template <typename Ty, size_t N, typename HashFunction = BasicHashFunc<Ty>>
class Chaining
{
public:
Chaining() = default;
~Chaining() = default;
void Insert(Ty item)
{
int hashAddr = hashfunc(item) % N;
_items[hashAddr].push_back(item);
}
void Search(Ty key) const
{
int hashAddr = hashfunc(key) % N;
for (auto it = _items[hashAddr].begin(); it != _items[hashAddr].end(); ++it)
{
if (*it == key) /* 탐색 성공 */
{
cout << "[" << hashAddr << "] : " << key << endl;
return;
}
}
cout << "Do Not Exist. " << endl; /* 탐색 실패 */
}
void Remove(Ty key)
{
int hashAddr = hashfunc(key) % N;
auto it = _items[hashAddr].begin();
for (; it != _items[hashAddr].end(); ++it)
{
if (*it == key) /* 탐색 성공 */
{
_items[hashAddr].erase(it);
return;
}
}
/* 탐색 실패 */
}
size_t GetLoadingFactor() const { return _size / _capacity; }
size_t GetSize() const { return _size; }
size_t GetCapacity() const { return _capacity; }
private:
list<Ty> _items[N];
size_t _size = 0;
const size_t _capacity = N;
HashFunction hashfunc;
};
마치며
다음 포스팅에는 이차조사법과 이중 해쉬
좋은 해쉬 함수에 대해서 설명하겠습니다.
'자료구조 > 자료구조 이론' 카테고리의 다른 글
| [C++/자료구조] 자료구조에서의 좋은 해쉬함수 (1) | 2024.01.26 |
|---|---|
| [C++/자료구조] 이차조사법과 이중해쉬 (Quadratic Probing, Double Hash) (0) | 2024.01.26 |
| [C++/자료구조] 해쉬 입문 (1) | 2024.01.25 |
| [C++] 자가 균형 트리: 레드블랙 트리 (上: 삽입전략) (0) | 2024.01.24 |
| [C++] 자가 균형 트리: AVL 트리 (0) | 2024.01.23 |




