개발하는 리프터 꽃게맨입니다.
[C++] 자가 균형 트리: 레드블랙 트리 (上: 삽입전략) 본문
레드블랙 트리 기본
1) 개요

레드블랙 트리(이하 RB트리)는 AVL트리와 같은 '자가 균형 이진 탐색 트리'입니다.
삽입 및 삭제 시 스스로 균형을 유지하여 탐색에 있어 평균 O(log2 N) 만에 수행할 수 있도록 보장해 주죠.
멀쩡한 AVL 트리가 있는데 레드블랙 트리는 왜 등장했을까요?
AVL 트리는 매우 엄격한 균형을 유지하는 트리이며, 오버헤드가 큽니다.
특히 높이를 계산하는 과정은 재귀를 통해 일어나기 때문에 자료가 많으면 많을수록 삽입/삭제 시 소모되는 계산 오버헤드는 커지게 되죠.
(높이 계산을 매번 하지 않고 노드 자체에 저장하는 최적화 방법이 존재합니다.)
그러나 RB트리는 덜 엄격한 균형을 이룹니다.
심지어 balance factor를 균형의 규칙으로 사용하지도 않기에
시간적, 공간적인 면에서도 이점이 있죠.
그렇기 때문에 삽입과 삭제에 있어서 AVL 트리보다 빠릅니다.
물론 조금 불균형한 트리이기 때문에, AVL 트리보다 탐색에 있어서 매우 조금 느릴 수 있습니다.
탐색이 잦은 자료구조로는 AVL 트리가 알맞을 가능성이 있고
삽입/삭제가 잦은 자료구조는 RB트리가 알맞을 가능성이 높습니다.
현실 프로그램에서는 데이터의 삽입, 삭제가 빈번하게 일어나기에
RB트리를 선택되곤 하죠.
2) 기본

RB트리는 외형상으로는 이진 탐색 트리와 동일하지만, 가장 큰 특징은 노드에 색상이 존재한다는 겁니다.
색상이 존재하는 것을 제외하고는 BST와 동일합니다.
왼쪽 자식 < 부모 < 오른쪽 자식
이란 규칙이 동일하게 적용되죠.
RB트리가 균형을 위지 하기 위한 성질은 다음과 같습니다.
(1) 각 노드는 빨강 혹은 검정의 색상을 가진다.
(2) 각 외부 노드로 가는 검정 노드의 수는 같다.
(3) 새로 삽입되는 노드는 항상 빨강 노드이다.
(4) 경로상에 2개의 빨강 노드가 연속해서 등장할 수 없다.
(5) 루트 노드는 항상 검정 노드이다.
(6) nullptr는 NIL 노드라고 부르고 검정 노드로 여긴다.
이 성질을 만족하면서 삽입/삭제 알고리즘을 작성하면 균형 트리를 구현할 수 있습니다.
레드블랙 트리의 삽입 전략
1) 노드 및 트리 기본 구조

노드와 RB트리의 기본 구조입니다.
구현하는 방법은 여러 가지이지만
저는 노드가 부모의 정보를 가지고 있도록 하는 것이 구현 난이도가 조금 더 쉽다고 생각해서
위와 같이 구현했습니다.
Color는 enum으로 정의했는데, 이는 가독성을 위한 것이고
비트 플래그를 사용하면 메모리 공간을 아낄 수 있습니다.
실제로 구현할 때는 비트 플래그를 사용하시길 바랍니다.
또, 매번 RBNode라고 쓰면 번거로워서 Node를 사용하도록 했습니다.
2) 기본 삽입

삽입에 바탕이 되는 기본 삽입 함수입니다.
재귀를 사용하지 않는 이진트리와 모습이 유사합니다.
주의할 점은 삽입할 노드가 항상 RED여야 한다는 것이고
노드의 부모 또한 꼼꼼히 관리해줘야 한다는 것이죠.
근데 이렇게 하면 BST랑 정말 똑같은 자료구조고
어떻게 균형을 맞출지 이야기해 보겠습니다.

삽입에서 신경 써야 할 부분은 이 경우입니다.
같은 경로에 빨강 노드가 연속적으로 등장할 경우
이것을 해결하기 위한 방법은 2 가지 있습니다.
바로 컬러링과 회전이죠.
상황에 따라서 어떤 방법을 적용해야 하는지 다릅니다.
3) 컬러링: 삼촌 노드가 빨강 노드일 경우

삽입한 노드가 70이라고 생각해 봅시다.
50은 70은 부모
30은 70의 조부모
20은 70의 삼촌입니다.
삼촌이 빨강 노드일 경우 노드의 색상만 바꾸는 컬러링을 수행합니다.

조부모를 빨강노드로,
삼촌과 부모를 검정노드로 설정하는 것이죠.
이러면 연속된 빨강노드를 없앨 수 있습니다.
참고로 루트 노드는 항상 검정 노드여야 하기 때문에, 위 그림에서 30은 검정 노드로 바꿔줘야만 합니다.
물론 이건 코드 한 줄이면 해결되겠죠.
4) 회전: 삼촌 노드가 검정 노드일 경우
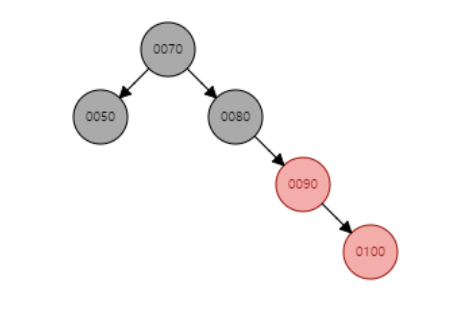
이 경우는 어떤가요?
삼촌 노드가 검정 노드입니다. (NIL 노드는 검정 노드로 여김)
그러면 컬러링으로 성질을 만족할 수 없습니다.
이 상황에서는 회전을 사용합니다.
AVL 트리에서 사용했던, LL 회전, RL 회전. LR 회전. RR 회전을 사용하시면 됩니다.
단, 노드가 부모 노드를 기억하고 있기 때문에, 이점은 신경 써주셔야 합니다.

회전 함수에 대한 구현입니다.
부모 자식 연결이 번거롭기에
구현할 때 실수하지 않도록 조심해야 합니다.

회전이 끝나면
삽입 노드의 부모의 자식들을 모두 빨강 노드, 부모는 검정 노드로 바꿔줍니다.
5) 삽입 코드 구현

이제 균형을 맞춰봅시다.
앞서 말한 빨강 노드가 2개 연이어 나올 경우에 유의하면서 설계하면 됩니다.

부모와 조부모를 설정합니다.
빨강 노드가 연이어 2개 나왔다는 것은 적어도 레벨이 3 이상이라는 것을 뜻합니다.
루트노드는 무조건 검정 노드이기 때문이죠.

삼촌을 설정해 줍니다.
삼촌은 nullptr 일 수 있으니
color도 따로 저장합니다.
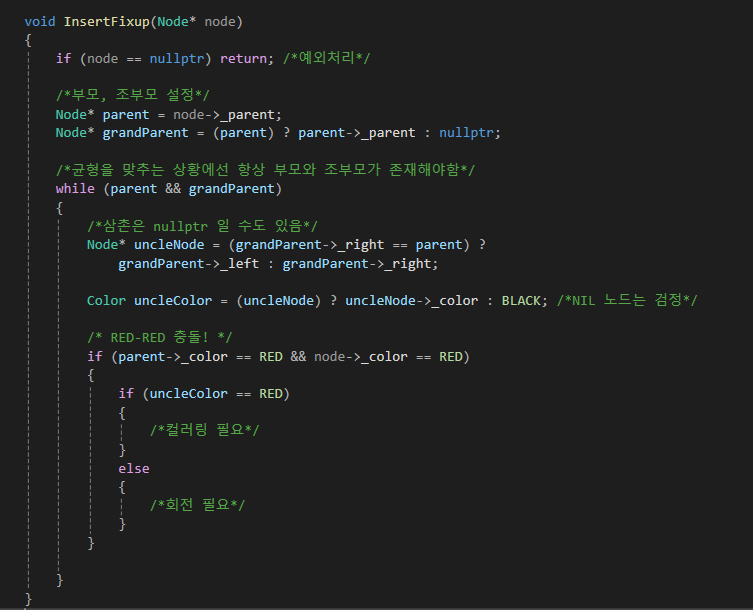
부모와 자신 노드가 RED RED 인 경우는 충돌이 난 경우이며, 트리의 재구성이 필요합니다.
uncleColor가 RED이면 컬러링을, 아니면 회전을 하면 되겠죠?
컬러링 먼저 작성해 봅시다.

조부모 = 빨강
삼촌과 부모 = 검정
조부모가 루트일 수도 있기에 함수 끝에 _root는 항상 검정이 될 수 있도록 코드를 추가했습니다.
이제 회전 부분을 작성해 봅시다.

AVL 트리처럼 회전시켜 주고
색상설정을 해줍니다.

마지막으로 계층을 1 레벨씩 올려주는 코드를 추가합니다.
회전과 컬러링의 과정에서 위쪽 계층에서 성질이 무너졌을 수 있기 때문에
계층을 쭉 올라가면서 확인하고 필요하다면 또 회전 및 컬러링을 하는 것이죠.
그래서 while 루프를 이용한 것입니다.
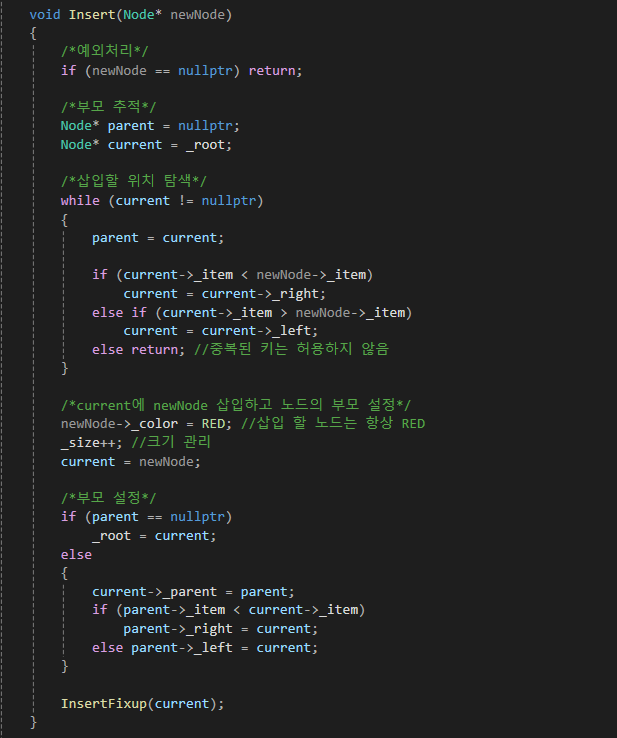
그리고 Insert 함수 맨 마지막에 균형을 잡기 위한 함수
InsertFixup을 추가해 주시면 알아서 균형을 잡습니다.
//색상 코드
enum Color {RED, BLACK};
//노드
template <typename Ty>
struct RBNode
{
RBNode(Ty item) : _item(item) {}
~RBNode() = default;
public:
Ty _item = Ty();
Color _color;
RBNode* _parent = nullptr;
RBNode* _left = nullptr;
RBNode* _right = nullptr;
};
//RB트리
template <typename Ty>
class RedBlackTree
{
using Node = RBNode<Ty>;
public:
RedBlackTree() = default;
~RedBlackTree() = default;
void LevelorderTraversal()
{
queue<pair<Node*, int>> q;
q.push(make_pair(_root, 1));
while (!q.empty())
{
Node* hereNode = q.front().first;
int hereLevel = q.front().second;
q.pop();
cout << "[" << hereLevel << "] : " << hereNode->_item << endl;
if (hereNode->_left != nullptr)
q.push(make_pair(hereNode->_left, hereLevel + 1));
if (hereNode->_right != nullptr)
q.push(make_pair(hereNode->_right, hereLevel + 1));
}
}
void Insert(Node* newNode)
{
/*예외처리*/
if (newNode == nullptr) return;
/*부모 추적*/
Node* parent = nullptr;
Node* current = _root;
/*삽입할 위치 탐색*/
while (current != nullptr)
{
parent = current;
if (current->_item < newNode->_item)
current = current->_right;
else if (current->_item > newNode->_item)
current = current->_left;
else return; //중복된 키는 허용하지 않음
}
/*current에 newNode 삽입하고 노드의 부모 설정*/
newNode->_color = RED; //삽입 할 노드는 항상 RED
_size++; //크기 관리
current = newNode;
/*부모 설정*/
if (parent == nullptr)
_root = current;
else
{
current->_parent = parent;
if (parent->_item < current->_item)
parent->_right = current;
else parent->_left = current;
}
InsertFixup(current);
}
private:
void InsertFixup(Node* node)
{
if (node == nullptr) return; /*예외처리*/
/*부모, 조부모 설정*/
Node* parent = node->_parent;
Node* grandParent = (parent) ? parent->_parent : nullptr;
/*균형을 맞추는 상황에선 항상 부모와 조부모가 존재해야함*/
while (parent && grandParent)
{
/*삼촌은 nullptr 일 수도 있음*/
Node* uncleNode = (grandParent->_right == parent) ?
grandParent->_left : grandParent->_right;
Color uncleColor = (uncleNode) ? uncleNode->_color : BLACK; /*NIL 노드는 검정*/
/* RED-RED 충돌! */
if (parent->_color == RED && node->_color == RED)
{
if (uncleColor == RED)
{
/*컬러링 필요*/
grandParent->_color = RED;
parent->_color = BLACK;
uncleNode->_color = BLACK;
}
else
{
/*회전 필요*/
if (grandParent->_left == parent) /*L 불균형*/
{
if (parent->_right == node) /*LR 불균형*/
LeftRotation(parent);
RightRotation(grandParent);
}
else /*R 불균형*/
{
if (parent->_left == node) /*RL 불균형*/
RightRotation(parent);
LeftRotation(grandParent);
}
/* 색상 설정 */
node->_parent->_color = BLACK;
node->_parent->_left->_color = RED;
node->_parent->_right->_color = RED;
}
}
node = parent;
parent = (node) ? node->_parent : nullptr;
grandParent = (parent) ? parent->_parent : nullptr;
}
_root->_color = BLACK;
}
void RightRotation(Node* node)
{
Node* child = node->_left;
node->_left = child->_right;
/*node->_left의 부모 설정*/
if (child->_right)
child->_right->_parent = node;
/*node의 부모와 child 연결*/
child->_parent = node->_parent;
if (node->_parent)
node->_parent->_left = child;
else _root = child; /*부모가 없으면 child는 루트노드*/
child->_right = node;
node->_parent = child;
}
void LeftRotation(Node* node)
{
Node* child = node->_right;
node->_right = child->_left;
/*node->_left의 부모 설정*/
if (child->_left)
child->_left->_parent = node;
/*node의 부모와 child 연결*/
child->_parent = node->_parent;
if (node->_parent)
node->_parent->_right = child;
else _root = child; /*부모가 없으면 child는 루트노드*/
child->_left = node;
node->_parent = child;
}
private:
Node* _root = nullptr;
size_t _size = 0;
};

대충 값들을 넣고 중위순회를 해봤습니다.
AVL처럼 엄격하게 균형을 잡지는 않죠?

그림으로 본다면 이런 꼴이 나옵니다.
어느 정도 균형을 잡으면서
삽입/삭제 속도를 끌어올린 자료구조라고 보시면 되겠습니다.
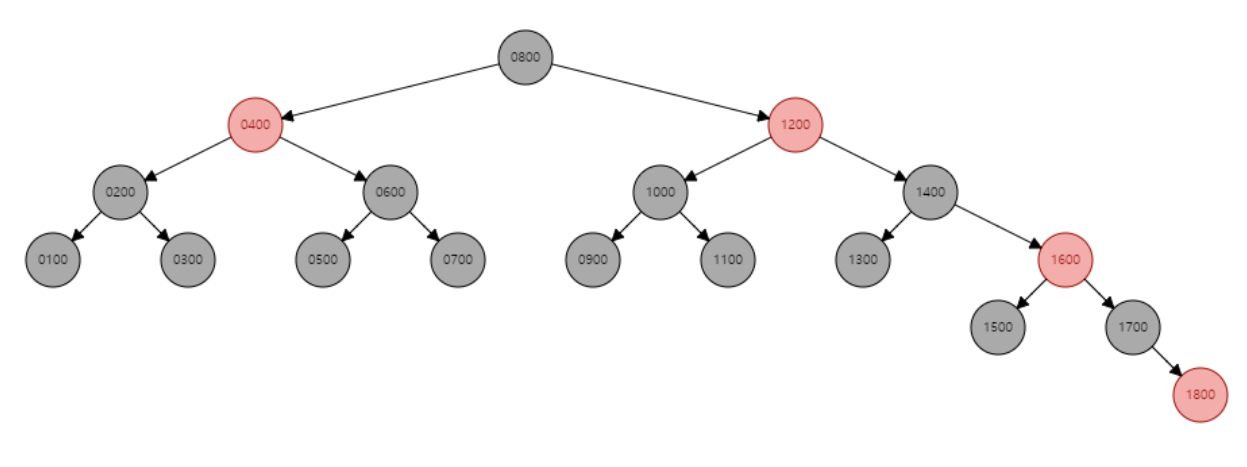
자료를 조금 더 넣어봤습니다.
이 정도면 어느 정도 균형 잡힌 트리라고 할 수 있죠.
탐색의 경우 알고리즘이 이진탐색트리와 완전히 같습니다.
이제 삭제를 다뤄야 하는데, 또 꽤 긴 내용을 서술할 것이기 때문에
자세한 것은 다음 포스팅에 이어서 작성하겠습니다.
'자료구조 > 자료구조 이론' 카테고리의 다른 글
| [C++/자료구조] 선형조사법과 체이닝 해쉬 (1) | 2024.01.26 |
|---|---|
| [C++/자료구조] 해쉬 입문 (1) | 2024.01.25 |
| [C++] 자가 균형 트리: AVL 트리 (0) | 2024.01.23 |
| [C++] 트리와 이진 탐색 트리 (Binary Shearch Tree) (0) | 2024.01.23 |
| [C++] 연결리스트 (단순/환형/이중 연결리스트) (1) | 2024.01.23 |




