개발하는 리프터 꽃게맨입니다.
[C++] 자가 균형 트리: AVL 트리 본문
1. 이진 탐색 트리의 문제점
이진 탐색 트리는 매우 효율적인 자료구조입니다.
'균형 트리'라는 전제하에 삽입, 삭제, 탐색이 모두 O(log2 N)만을 소모합니다.
그런데, 이진 탐색 트리는 '균형' 을 보장하지 않습니다.

만약 삽입을 하다 이런 트리 구조가 나왔다면, 시간 복잡도가 O(N) 에 가까워지는 것이죠.
따라서 이진 탐색 트리에서는 균형을 유지하는 것이 매우 중요하여,
여러가지 스스로 균형을 잡은 자가 균형 트리에 대해서 알아보도록 하겠습니다.
2. AVL 트리
1) 개요
AVL 트리는 이진 탐색 트리에서 한 가지 조건을 더 추가합니다.
왼쪽 서브트리와 오른쪽 서브 트리의 높이 차이가 1 이하
AVL 트리는 항상 균형 트리를 보장되기 때문에 탐색이 O(log2 n) 만에 완료됩니다.
2) Balance Factor
먼저 Balance Factor 를 정의합니다.
Balance_Factor = 왼쪽서브트리높이 - 오른쪽서브트리
로 정의됩니다.
그러면 먼저 높이를 구하는 함수를 구현해야 합니다.

이 함수를 이용해서 balance factor를 구합니다.

이 함수로 인해 balance factor를 구할 수 있게 되었고,
balance factor의 절댓값이 2이상이면 불균형 트리임을 알 수 있습니다.
2 이상일 경우 왼쪽 서브트리의 불균형
-2 이하일 경우 오른쪽 서브트리의 불균형인 것이죠.
3) 회전
그러면 불균형 트리가 존재할 시 어떻게 조치해야 하는지에 대해서 알아봅시다.
(1) LL 불균형
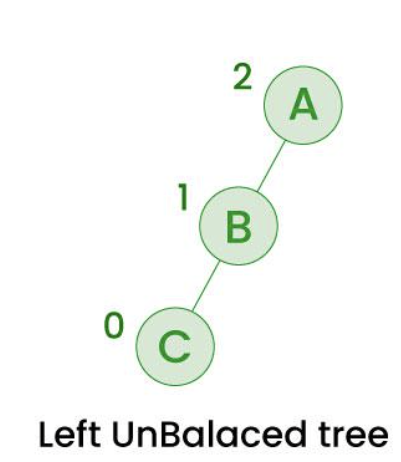
루트 노드 A에서 부터 왼쪽 왼쪽으로 불균형한 트리입니다.
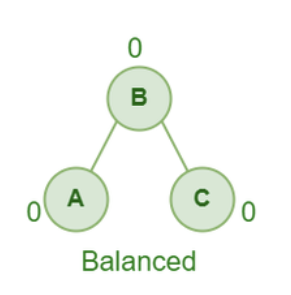
이 경우 B를 루트로 올리고 A를 B의 오른쪽 자식으로 바꾸면 됩니다.
B을 오른쪽으로 회전시키는 것과 같다하여, Right Rotation 이라고 부릅니다.

(2) RR 불균형
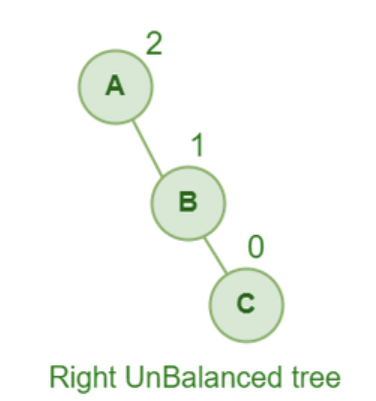
RR 불균형입니다. LL의 반대입니다.
A에 대해서 왼쪽 회전을 해주면 됩니다.
(3) LR 불균형
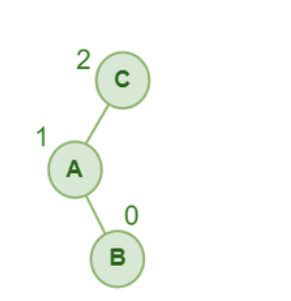
LR 불균형 입니다.
C에 대해서 balance factor 가 2 이상이고
왼쪽 자식의 오른쪽 자식의 nullptr 이 아닐 경우 입니다.
A에 대해서 Left Rotation 1번을 하면 LL 불균형이 됩니다. C에 대해서 Right Rotation 1번 해주시면 됩니다.
(4) RL 불균형
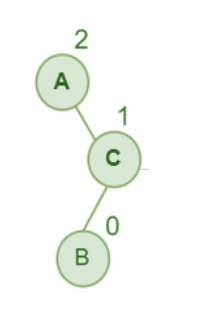
마지막으로 RL 불균형입니다.
C에 대해서 Right Rotation 1번과 A에 대해서 Left Rotation 1번 해주시면 됩니다.
(5) Rotation 함수와 SetBalance 함수
[1] RightRotation

LL 불균형에서 사용하는 회전 함수입니다.
A를 기준으로 RightRotation하면
A의 왼쪽자식의 오른쪽 서브트리를 A의 왼쪽 링크에 넘기고
B가 A를 오른쪽 자식으로 둡니다.
[2] LeftRotation

RightRotation과 반대로 작용합니다.
[3] SetBalance

불균형을 체크하여 균형을 잡아주는 함수입니다.
노드 A를 기준으로 불균형을 체크하고, 불균형을 발견한 경우 다음과 같이 동작합니다.
- 왼쪽 불균형인 경우
-> 왼쪽 노드에 대해서 균형 체크를 한 번 더 했을 때 오른쪽 높이가 더 크다면 LR 불균형이므로 왼쪽 회전
-> 오른쪽 회전
- 오른쪽 불균형인 겨우
-> 오른쪽 노드에 대해서 균형 체크를 한 번 더 했을 때 왼쪽 높이가 더 크다면 RL 불균형이므로 오른쪽 회전
-> 왼쪽 회전
(6) 완성
트리의 불균형이 발생하는 상황은 단 두 가지입니다.
삽입시와 삭제시
삽입과 삭제시 return 부분만 SetBalance로 균형을 체크해주면 자동으로 균형이 잡힙니다.


(7) 테스트 및 전체 코드

중복 없는 숫자 10000개를 뽑아서 트리에 삽입해봤습니다.
log2 1000 이 대략 13.2 정도 됩니다.
저는 레벨을 1부터 설정했으니
레벨 순회를 했을 때, 15 레벨 정도 뜨면 될 것 같습니다.
실제로 실험해봤을 때, 16레벨이 나왔습니다.
이정도면 어느정도 균형이 잡혔다고 말할 수 있습니다.
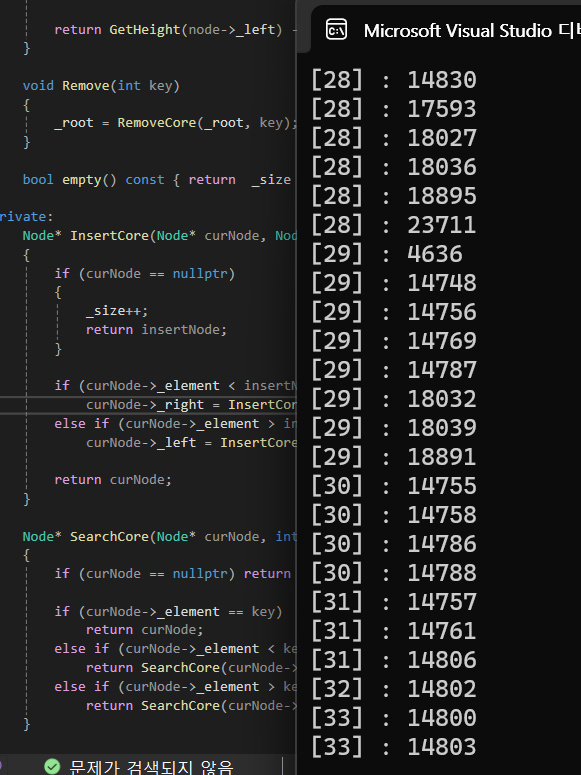
일반적인 BST 로 삽입한 모습입니다.
똑같이 10000개의 데이터를 넣었는데 33레벨까지 나옵니다.
아무래도 이진 탐색 트리의 시간복잡도는 높이를 h라고 했을 때 O(h) 이니,
10000개의 데이터만 넣어도 시간적으로는 2배의 차이가 나는 것이죠.
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
template <typename Ty>
struct Node
{
Node(Ty item) : _element(item) {}
~Node() = default;
public:
//데이터 영역
Ty _element = Ty();
//링크 영역
Node* _left = nullptr;
Node* _right = nullptr;
};
template <typename Ty>
class AVL
{
using Node = Node<int>;
public:
AVL() = default;
~AVL() = default;
Node* GetRoot() const { return _root; }
void Insert(Node* insertNode)
{
_root = InsertCore(_root, insertNode);
}
Node* Search(int key)
{
return SearchCore(_root, key);
}
void PreorderTraversal(Node* node)
{
if (node != nullptr)
{
cout << node->_element << endl;
PreorderTraversal(node->_left);
PreorderTraversal(node->_right);
}
}
void InorderTraversal(Node* node)
{
if (node != nullptr)
{
InorderTraversal(node->_left);
cout << node->_element << " " << endl;
InorderTraversal(node->_right);
}
}
void PostorderTraversal(Node* node)
{
if (node != nullptr)
{
PostorderTraversal(node->_left);
PostorderTraversal(node->_right);
cout << node->_element << " " << endl;
}
}
void LevelorderTraversal(Node* node)
{
queue<pair<Node*, int>> q;
q.push(make_pair(node, 1));
while (!q.empty())
{
Node* hereNode = q.front().first;
int hereLevel = q.front().second;
q.pop();
cout << "[" << hereLevel << "] : " << hereNode->_element << endl;
if (hereNode->_left != nullptr)
q.push(make_pair(hereNode->_left, hereLevel + 1));
if (hereNode->_right != nullptr)
q.push(make_pair(hereNode->_right, hereLevel + 1));
}
}
int GetHeight(Node* node)
{
if (node == nullptr)
return 0;
int leftHeight = GetHeight(node->_left);
int rightHeight = GetHeight(node->_right);
return 1 + max(leftHeight, rightHeight);
}
int GetBalanceFactor(Node* node)
{
if (node == nullptr)
return 0;
return GetHeight(node->_left) - GetHeight(node->_right);
}
void Remove(int key)
{
_root = RemoveCore(_root, key);
}
bool empty() const { return _size == 0; }
private:
Node* InsertCore(Node* curNode, Node* insertNode)
{
if (curNode == nullptr)
{
_size++;
return insertNode;
}
if (curNode->_element < insertNode->_element)
curNode->_right = InsertCore(curNode->_right, insertNode);
else if (curNode->_element > insertNode->_element)
curNode->_left = InsertCore(curNode->_left, insertNode);
return SetBalance(curNode);
}
Node* SearchCore(Node* curNode, int key)
{
if (curNode == nullptr) return nullptr;
if (curNode->_element == key)
return curNode;
else if (curNode->_element < key)
return SearchCore(curNode->_right, key);
else if (curNode->_element > key)
return SearchCore(curNode->_left, key);
}
Node* RemoveCore(Node* curNode, int key)
{
if (curNode == nullptr) return nullptr;
if (curNode->_element < key)
curNode->_right = RemoveCore(curNode->_right, key);
else if (curNode->_element > key)
curNode->_left = RemoveCore(curNode->_left, key);
else
{
if (curNode->_right == nullptr)
{
_size--;
if (curNode->_left == nullptr)
{
//경우 1:
delete curNode;
return nullptr;
}
//경우 2-1:
Node* rNode = curNode->_left;
delete curNode;
return rNode;
}
else if (curNode->_left == nullptr)
{
//경우 2-2:
_size--;
Node* rNode = curNode->_right;
delete curNode;
return rNode;
}
else
{
//경우 3:
Node* successor = curNode->_right;
while (successor->_left != nullptr)
successor = successor->_left;
curNode->_element = successor->_element;
curNode->_right = RemoveCore(curNode->_right, successor->_element);
}
}
return SetBalance(curNode);
}
Node* LeftRotation(Node* A)
{
Node* B = A->_right;
A->_right = B->_left;
B->_left = A;
return B;
}
Node* RightRotation(Node* A)
{
Node* B = A->_left;
A->_left = B->_right;
B->_right = A;
return B;
}
Node* SetBalance(Node* A)
{
int bf = GetBalanceFactor(A);
if (bf > 1) //왼쪽 불균형
{
if (GetBalanceFactor(A->_left) < 0)
{
A->_left = LeftRotation(A->_left);
}
return RightRotation(A);
}
else if (bf < -1) //오론쪽 불균형
{
if (GetBalanceFactor(A->_right) > 0)
{
A->_right = RightRotation(A->_right);
}
return LeftRotation(A);
}
return A;
}
public:
Node* _root = nullptr;
int _size = 0;
};
2. 마무리
다음 포스팅에는 다른 자가 균형 트리인
2-3 트리, 2-3-4 트리를 구현해보고
그 다음 포스팅으로 RB트리를 구현해보도록 하겠습니다.
'자료구조 > 자료구조 이론' 카테고리의 다른 글
| [C++/자료구조] 선형조사법과 체이닝 해쉬 (1) | 2024.01.26 |
|---|---|
| [C++/자료구조] 해쉬 입문 (1) | 2024.01.25 |
| [C++] 자가 균형 트리: 레드블랙 트리 (上: 삽입전략) (0) | 2024.01.24 |
| [C++] 트리와 이진 탐색 트리 (Binary Shearch Tree) (0) | 2024.01.23 |
| [C++] 연결리스트 (단순/환형/이중 연결리스트) (1) | 2024.01.23 |




