개발하는 리프터 꽃게맨입니다.
[C++] 연결리스트 (단순/환형/이중 연결리스트) 본문
[ 목차 ]
개요
1. 리스트란?
리스트는 자료를 정리하는 방법 중 하나입니다.
항목이 '연속적으로' 저장되어 있는 자료구조의 가장 기본적인 한 형태라고 할 수 있죠.
대부분의 언어에서 기본적으로 제공하는 '배열' 역시 '리스트'의 한 종류 입니다
그리고 '리스트'를 구현하는 방법이 하나 더 있는데, 그것이 연결 리스트입니다.
2. 연결리스트
연결리스트는 노드라는 데이터 단위가 존재하고, 노드 내부에는 데이터가 연결되는 데이터 영역, 그리고 다른 노드를 가리키는 링크 영역이 존재합니다.
저장하고 싶은 데이터를 데이터 영역에 저장하고, 링크 영역에서 링크라는 연결이 다른 노드를 가리킵니다.

이런 방식으로
메모리가 링크라는 줄로 연결된 상태입니다.
이런 링크라는 표현은 다른 여러 가지의 자료구조를 구현하는데 많이 사용되는 개념입니다.
연결리스트는 배열처럼 연속적으로 저장된 데이터로 접근하는 것이 아니고, 메모리 상에 데이터가 흩어져있고 링크를 통해 데이터를 연결하여 하나로 묶는 자료구조입니다.
이런 링크를 표현하는 것은 포인터로 구현합니다.
이러한 링크의 장점은 어떤 노드를 삭제한다고 했을 때, 노드의 위치를 알고있다면 O(1)의 복잡도가 소모됩니다.
배열 리스트의 경우 중간의 데이터를 제거했을 때, 뒤에 있는 데이터를 다 당겨와야 하기에, O(N)의 복잡도가 소모되지만, 연결리스트의 경우 링크만 바꿔주면 되기 때문입니다.
중간 삽입시에도 연결 리스트는 O(1) 만에 이루어집니다.
3. 연결 리스트의 구조

데이터와 링크를 저장하는 것을 노드라고 합니다.
연결 리스트는 노드들의 집합이고
노드의 데이터 영역에 데이터가 저장, 노드의 링크 영역에 다음 노드에 대한 주소 정보가 들어갑니다.
보통 연결리스트의 경우 '중간 노드'로의 O(1) 접근이 불가능하기 때문에, 맨 앞 노드를 통해서 접근해야만 합니다.
그래서 선두 노드를 헤드(머리)라고 부릅니다.
그리고 마지막 노드는 테일(꼬리)라고 부릅니다.
해당 포스팅에서는 테일이라는 표현은 '이중 연결 리스트'에서만 사용합니다.
모든 리스트에서 헤드와 테일을 구현해서 더미 노드로 구현하는 경우도 있는데, 저는 그 방법을 사용하지 않습니다.
자세한 것은 다음 목차를 참고해주시길 바랍니다.
4. 연결 리스트의 종류
1) 단순 연결 리스트, 단방향 연결 리스트

하나의 방향으로만 연결되어 있는 가장 기본적인 연결 리스트입니다.
마지막 노드의 링크는 nullptr 입니다.
2) 원형 연결 리스트, 환형 연결 리스트
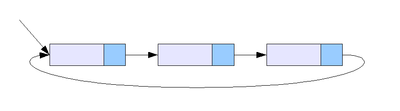
마지막 노드의 링크가 헤드를 가리키는 연결 리스트입니다.
3) 이중 연결 리스트
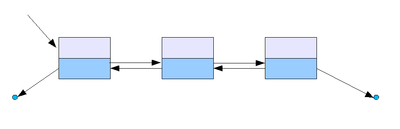
하나의 노드가 다음 노드 뿐만이 아니라
이전 노드도 가리키는 형태의 연결 리스트입니다.
환형으로도 구현할 수 있습니다.
단순 연결리스트의 추상화 (ADT)
1) 노드 구조
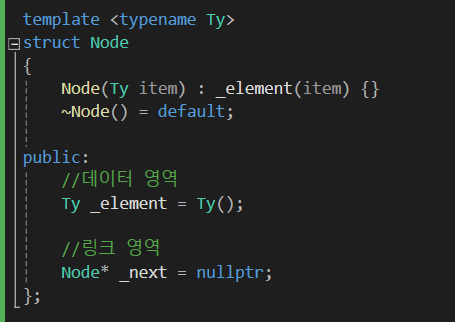
데이터 영역과 링크 영역이 존재합니다.
Node 는 class로 만들어도 struct로 만들어도 상관없습니다.
어짜피 데이터를 저장하는 용도로만 사용하니 struct으로 구현하는 게 좀 더 괜찮다고 봅니다.
2) 리스트의 구조
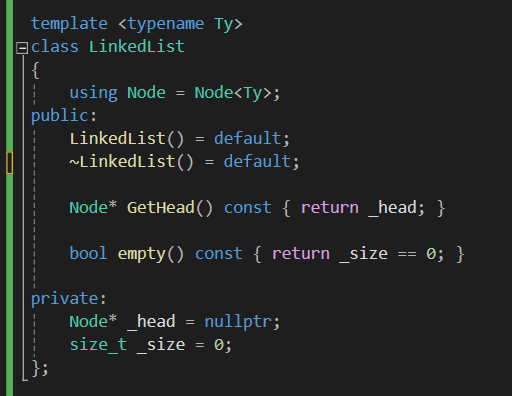
자료구조 답게 size를 카운팅 해주고
리스트 본체는 오직 head Node 만 가리킵니다.
나머지 node는 _head를 통해 접근합니다.
3) 삽입
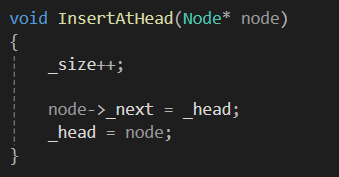
head 부분에 삽입을 하는 함수 하나
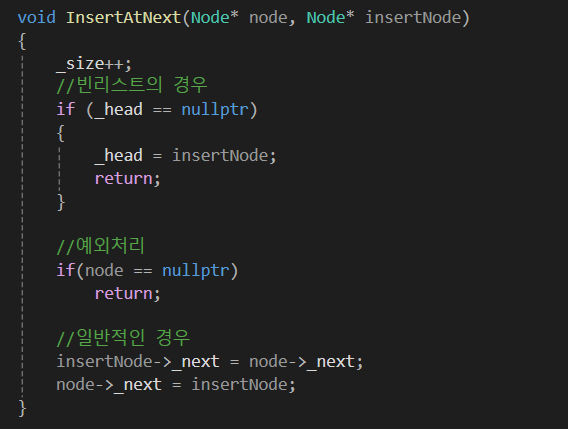
특정 노드를 지정해서 O(1) 만에 삽입하는 함수 입니다.
InsertAtNext의 경우 반드시 '리스트 내에 있는 노드'를 삽입해줘야만 하는데,
그걸 확인하는 과정은 O(N)이 소모되므로 굳이 따로 확인하지는 않았습니다.
특정 알고리즘을 추가하여 런타임에 확인하거나, 개발자 단에서 조심해서 사용하는 것이 좋을 것 같습니다.
4) 탐색
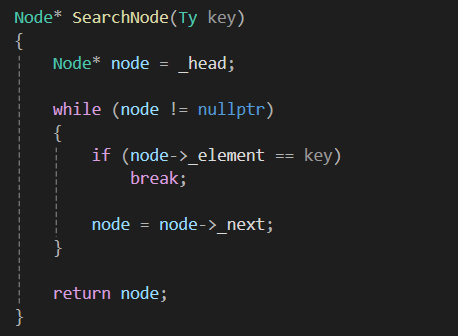
key 값을 통해 원하는 노드를 찾아내는 함수입니다.
node = node -> _next 라는 구문을 통해
리스트 전체를 순회할 수 있고
원하는 key값을 찾으면 Node 를 반환하고
차지 못하면 nullptr 를 반환합니다.
5) 삭제
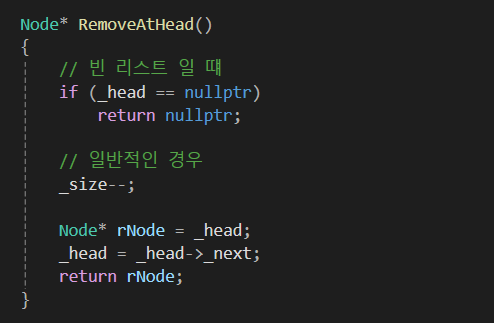
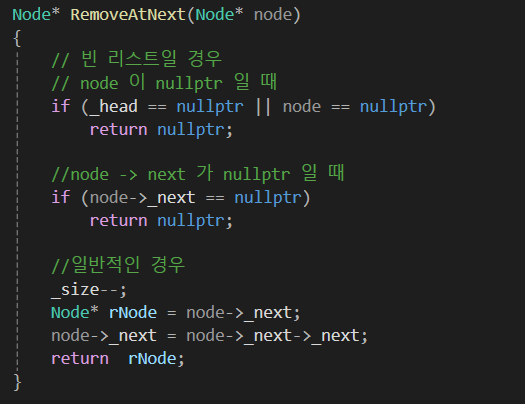
삭제 함수인데, 비교적 로직이 복잡합니다.
삭제 함수의 경우 삭제하고자 하는 함수의 이전 노드를 알아야합니다.
그래서 위 코드처럼 RemoveAtNext라는 함수를 통해 해당 노드의 다음 노드를 삭제하는 함수를 O(1)로 짤 수 있습니다.
만약 원하는 노드를 탐색해서 지우고 싶다고하면
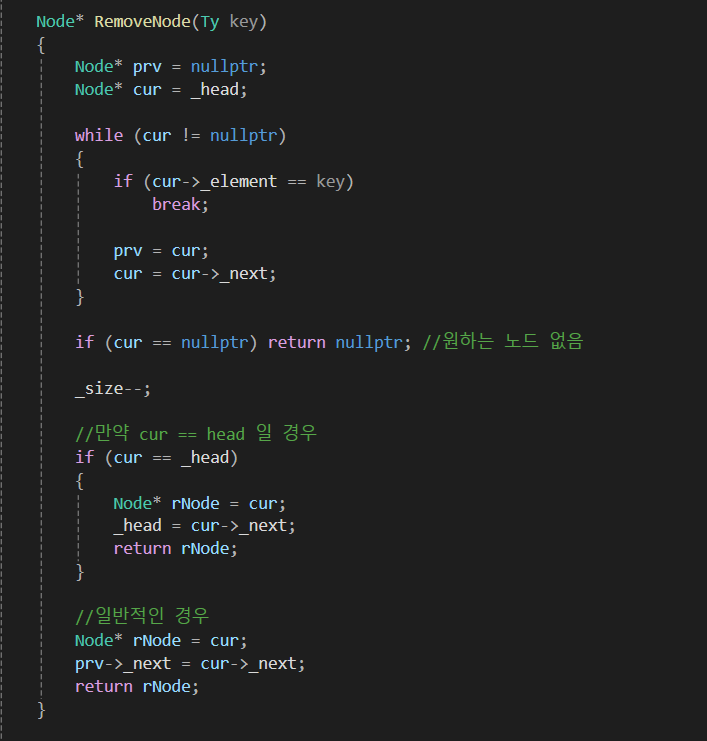
이런 식의 코드를 짤 수 있으며 O(N)의 시간이 걸립니다.
연결 리스트는 '원하는 노드 삭제'시 이전 노드 또한 알아야 하기 때문에,
삭제에 있어서 제약이 있을 수 있습니다.
그렇기 때문에, 일반적으로 '양방향 리스트'를 사용합니다.
!! 주의할 점 !!
해당 삭제 코드는 따로 메모리를 해제하지 않습니다.
이것은 취향 차이라고 생각하는데,
내가 외부에서 메모리를 할당해서 메모리는 따로 관리하고
연결리스트는 오로지 자료구조로의 역할만 시키고 싶을 경우 따로 delete 를 연결리스트 내부에서 하는 것이 아니라, 그냥 노드의 연결성만 바꾸는 형식으로 사용할 수 있습니다.
만약 위 코드에서 안전하게 메모리를 해제하고 싶다면 아래와 같은 코드를 따로 만들어 사용해야 합니다.
아니면 메모리 누수가 발생할 수 있습니다.
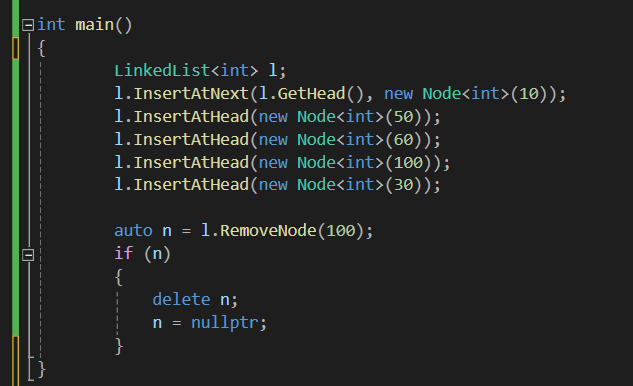
연결 리스트에서 해제를 할 경우 use-after-free 문제가 발생할 수 있고
반대의 경우 memory-leak 이 발생할 수 있습니다.
어떤 경우든 프로그래머가 잘 판단해서 설계하시면 되겠습니다.
6) 전체 코드
#include <iostream>
using namespace std;
template <typename Ty>
struct Node
{
Node(Ty item) : _element(item) {}
~Node() = default;
public:
//데이터 영역
Ty _element = Ty();
//링크 영역
Node* _next = nullptr;
};
template <typename Ty>
class LinkedList
{
using Node = Node<Ty>;
public:
LinkedList() = default;
~LinkedList() = default;
void InsertAtHead(Node* node)
{
_size++;
node->_next = _head;
_head = node;
}
void InsertAtNext(Node* node, Node* insertNode)
{
_size++;
//빈리스트의 경우
if (_head == nullptr)
{
_head = insertNode;
return;
}
//예외처리
if(node == nullptr)
return;
//일반적인 경우
insertNode->_next = node->_next;
node->_next = insertNode;
}
Node* SearchNode(Ty key)
{
Node* node = _head;
while (node != nullptr)
{
if (node->_element == key)
break;
node = node->_next;
}
return node;
}
Node* RemoveAtHead()
{
// 빈 리스트 일 떄
if (_head == nullptr)
return nullptr;
// 일반적인 경우
_size--;
Node* rNode = _head;
_head = _head->_next;
return rNode;
}
Node* RemoveAtNext(Node* node)
{
// 빈 리스트일 경우
// node 이 nullptr 일 때
if (_head == nullptr || node == nullptr)
return nullptr;
//node -> next 가 nullptr 일 때
if (node->_next == nullptr)
return nullptr;
//일반적인 경우
_size--;
Node* rNode = node->_next;
node->_next = node->_next->_next;
return rNode;
}
Node* RemoveNode(Ty key)
{
Node* prv = nullptr;
Node* cur = _head;
while (cur != nullptr)
{
if (cur->_element == key)
break;
prv = cur;
cur = cur->_next;
}
if (cur == nullptr) return nullptr; //원하는 노드 없음
_size--;
//만약 cur == head 일 경우
if (cur == _head)
{
Node* rNode = cur;
_head = cur->_next;
return rNode;
}
//일반적인 경우
Node* rNode = cur;
prv->_next = cur->_next;
return rNode;
}
Node* GetHead() const { return _head; }
bool empty() const { return _size == 0; }
private:
Node* _head = nullptr;
size_t _size = 0;
};
환형 연결리스트의 추상화 (ADT)
노드의 끝을 nullptr이 아니라 head를 가리키게 하는 방식입니다.
링크 관리만 잘해주면 단순 연결리스트와 구현이 크게 다르지 않습니다.
그러므로 굳이 설명하지 않습니다.
이중 연결리스트의 추상화 (ADT)
1) 노드 구조
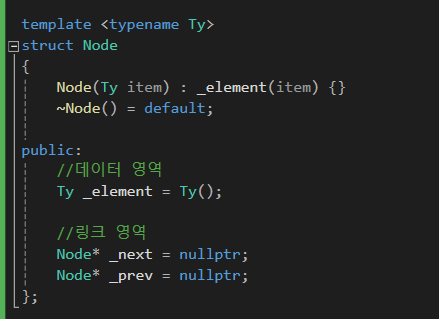
prev 가 하나 더 추가된 모습입니다.
2) 리스트의 구조
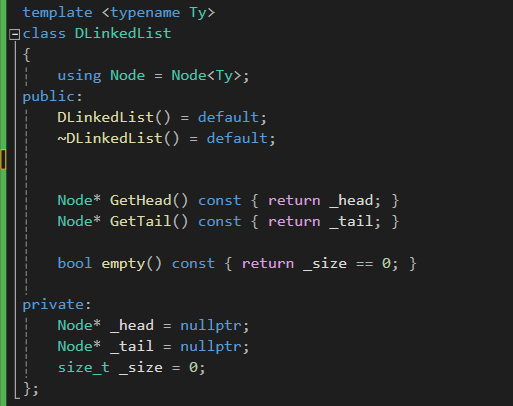
이중 연결 리스트는 tail의 관리가 조금 번거롭습니다.
이중 링크를 가지고 있기에
본인의 앞뒤 링크 관리에 더하여
이전 노드의 next 관리
이후 노드의 prev 관리
총 4개의 링크를 꼼꼼하게 관리하는 것이 중요합니다.
3) 삽입
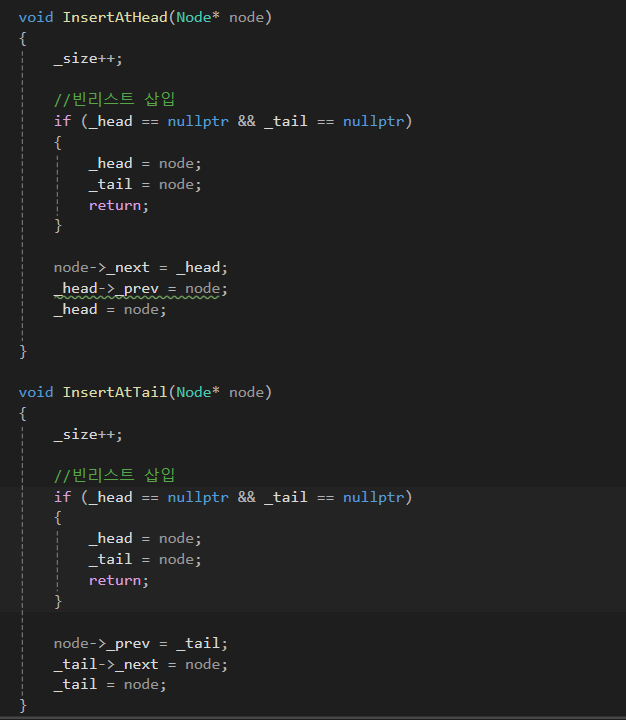
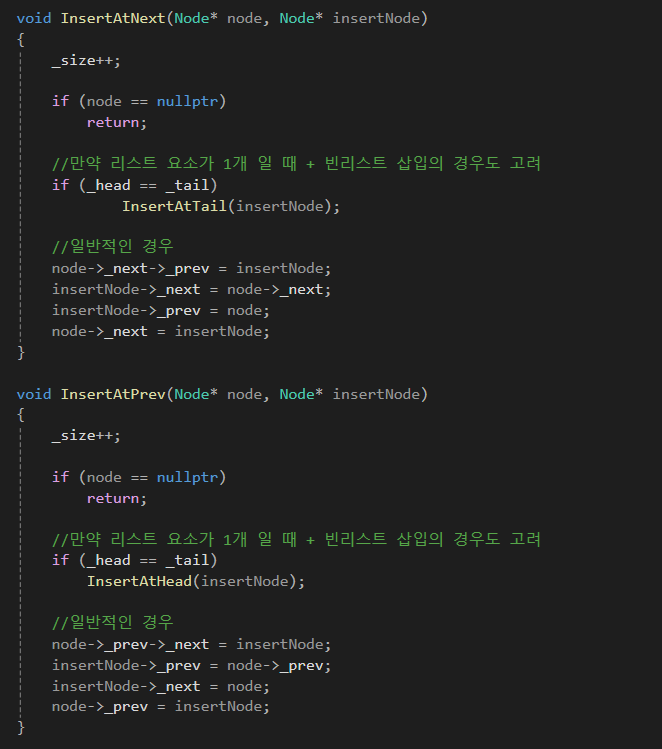
여러가지 삽입 코드입니다.
헤드, 테일 삽입 시 헤드 테일이 가리키는 노드를 잘 설정하는 것이 중요합니다.
4) 탐색
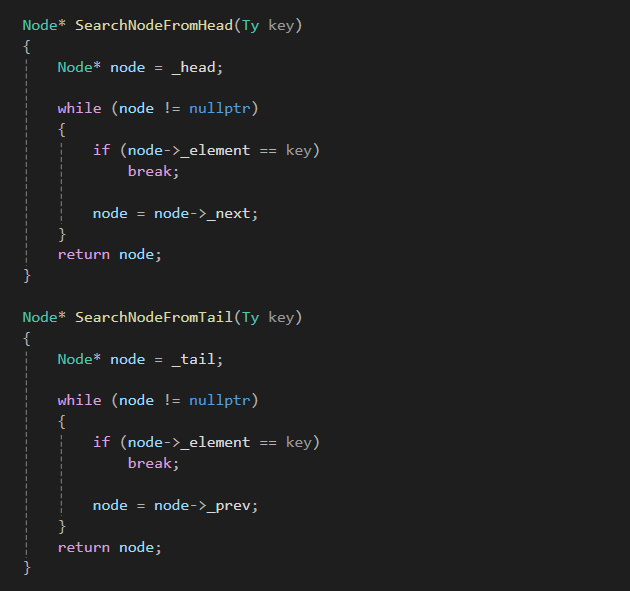
탐색은 단일 연결 리스트와 유사하게 진행됩니다.
이제 tail에서 prev로 이동하며 탐색하는 알고리즘도 고려할 수 있죠
5) 삭제
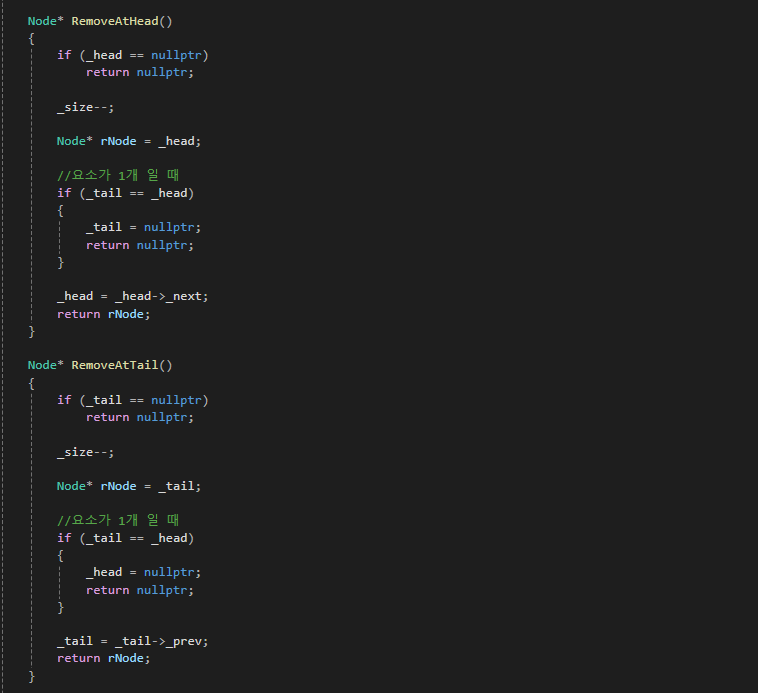
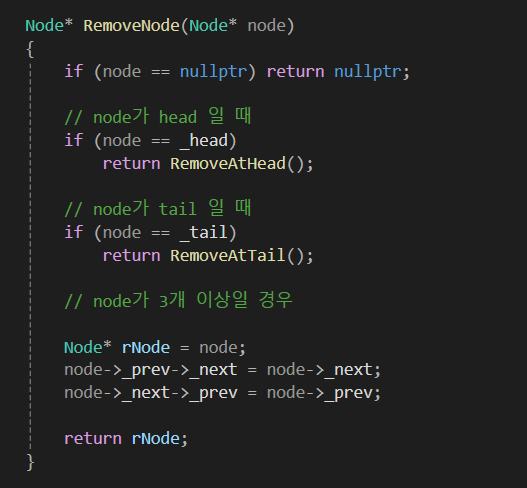
아무래도 이중 연결 리스트의 최대 장점이 '삭제 연산'이 매우 빠른 것 입니다.
노드의 주소만 제대로 알고 있으면
단일 연결 리스트와 다르게 원하는 노드를 O(1) 만에 삭제할 수 있습니다.
6) 전체 코드
template <typename Ty>
struct Node
{
Node(Ty item) : _element(item) {}
~Node() = default;
public:
//데이터 영역
Ty _element = Ty();
//링크 영역
Node* _next = nullptr;
Node* _prev = nullptr;
};
template <typename Ty>
class DLinkedList
{
using Node = Node<Ty>;
public:
DLinkedList() = default;
~DLinkedList() = default;
void InsertAtHead(Node* node)
{
_size++;
//빈리스트 삽입
if (_head == nullptr && _tail == nullptr)
{
_head = node;
_tail = node;
return;
}
node->_next = _head;
_head->_prev = node;
_head = node;
}
void InsertAtTail(Node* node)
{
_size++;
//빈리스트 삽입
if (_head == nullptr && _tail == nullptr)
{
_head = node;
_tail = node;
return;
}
node->_prev = _tail;
_tail->_next = node;
_tail = node;
}
void InsertAtNext(Node* node, Node* insertNode)
{
_size++;
if (node == nullptr)
return;
//만약 리스트 요소가 1개 일 때 + 빈리스트 삽입의 경우도 고려
if (_head == _tail)
InsertAtTail(insertNode);
//일반적인 경우
node->_next->_prev = insertNode;
insertNode->_next = node->_next;
insertNode->_prev = node;
node->_next = insertNode;
}
void InsertAtPrev(Node* node, Node* insertNode)
{
_size++;
if (node == nullptr)
return;
//만약 리스트 요소가 1개 일 때 + 빈리스트 삽입의 경우도 고려
if (_head == _tail)
InsertAtHead(insertNode);
//일반적인 경우
node->_prev->_next = insertNode;
insertNode->_prev = node->_prev;
insertNode->_next = node;
node->_prev = insertNode;
}
Node* SearchNodeFromHead(Ty key)
{
Node* node = _head;
while (node != nullptr)
{
if (node->_element == key)
break;
node = node->_next;
}
return node;
}
Node* SearchNodeFromTail(Ty key)
{
Node* node = _tail;
while (node != nullptr)
{
if (node->_element == key)
break;
node = node->_prev;
}
return node;
}
Node* RemoveAtHead()
{
if (_head == nullptr)
return nullptr;
_size--;
Node* rNode = _head;
//요소가 1개 일 때
if (_tail == _head)
{
_tail = nullptr;
return nullptr;
}
_head = _head->_next;
return rNode;
}
Node* RemoveAtTail()
{
if (_tail == nullptr)
return nullptr;
_size--;
Node* rNode = _tail;
//요소가 1개 일 때
if (_tail == _head)
{
_head = nullptr;
return nullptr;
}
_tail = _tail->_prev;
return rNode;
}
Node* RemoveNode(Node* node)
{
if (node == nullptr) return nullptr;
// node가 head 일 때
if (node == _head)
return RemoveAtHead();
// node가 tail 일 때
if (node == _tail)
return RemoveAtTail();
// node가 3개 이상일 경우
Node* rNode = node;
node->_prev->_next = node->_next;
node->_next->_prev = node->_prev;
return rNode;
}
Node* GetHead() const { return _head; }
Node* GetTail() const { return _tail; }
bool empty() const { return _size == 0; }
private:
Node* _head = nullptr;
Node* _tail = nullptr;
size_t _size = 0;
};연결리스트 vs 배열
그래서 연결리스트, 배열 어떤게 더 좋을까요?
연결리스트의 장단점을 먼저 체크 해봅시다.
1. 연결 리스트의 장점
1) 최대 용량이 정해져 있지 않다. 힙 메모리가 감당가능한 선에서 무한정으로 크기를 늘릴 수 있다.
2) 중간 삽입/삭제를 O(1) 만에 수행할 수 있다.
2. 연결 리스트의 단점
1) 삭제하고, 삽입할 노드의 위치를 알 경우에만 O(1)의 접근이 가능하고, 위치를 모를 경우 여전히 O(N)의 시간이 소모된다.
2) 논리적으로 연속된 자료구조지, 물리적으로 연속적인 메모리를 할당하지 않는다.
즉, 캐시 메모리의 지역적인 특성을 제대로 활용하지 못한다.
3) 추가적으로 링크 영역을 잡아먹기 때문에 노드 하나가 소모하는 데이터의 크기가 크다.
4) 메모리를 연속적으로 사용하지 않기 때문에, 메모리 파편화 현상이 발생할 수 있다.
5) 배열에 비해 알고리즘을 구현하기 어렵다.
사실 연결리스트는 장점보다는 단점이 많은 자료구조입니다.
그래서 실제로는 잘 사용하지 않죠.
그래서 여전히 자료구조의 기본기로 여겨지는 이유는
링크라는 논리적 구조 때문이라고 생각합니다.
링크로 이산적으로 흩어진 메모리에 접근한다는 아이디어는 앞으로 다룰 많은 자료구조 논리의
기초가 되는 셈이죠.
연결리스트를 구현할 수 있는 능력은 곧 자료구조의 기본기가 얼마나 잡혀있냐를 판가름 할 수 있는 능력이라고 생각합니다.
'자료구조 > 자료구조 이론' 카테고리의 다른 글
| [C++/자료구조] 선형조사법과 체이닝 해쉬 (1) | 2024.01.26 |
|---|---|
| [C++/자료구조] 해쉬 입문 (1) | 2024.01.25 |
| [C++] 자가 균형 트리: 레드블랙 트리 (上: 삽입전략) (0) | 2024.01.24 |
| [C++] 자가 균형 트리: AVL 트리 (0) | 2024.01.23 |
| [C++] 트리와 이진 탐색 트리 (Binary Shearch Tree) (0) | 2024.01.23 |





