개발하는 리프터 꽃게맨입니다.
좌표계 변환에 대한 삽질 본문
좌표계 변환에 대해서 잘 이해하지 못해서 다시 제대로 공부한 뒤 그 기록을 남긴다.
개인적으로 아핀변환이 더 직관적으로 이해된다고 생각하기 때문에..
좌표계 변환을 아핀 변환과 조금 섞어서 다시 표현해보도록 하겠다.
좌표계 변환 Change Of Coordinate Transformations
좌표계에는 여러 종류가 있다.
자신의 좌표계는 로컬 좌표계라고 하며
자신을 정의하는 좌표계도 존재할 수 있으므로 그러한 좌표계를 부모 좌표계
이런 식의 상속구조가 재귀적으로 정의될 수 있다.
물론 하나의 부모에서 여러 자식 좌표계가 존재할 수도 있다.
그러나 자식은 자신의 좌표계에서는 자기가 마치 표준 기저인 양 점들을 정의할 것이다.
로컬 좌표계만 가지고는 월드를 렌더링할 수가 없다.
결국 월드를 기준으로하는 모든 로컬좌표계를 변환해야 세계를 구성할 수 있고 렌더링을 수행할 수 있을 것이다.
그러므로 우리는 한 좌표계에서 정의된 점이 다른 좌표계에서 어떤 위치를 갖는지 알아야한다.
이를 좌표계 변환이라고 한다.
벡터 변환
좌표계 변환에 있어 벡터 변환과 점 변환은 다르게 동작하기 때문에. 벡터 변환부터 알아보도록 하자.

좌표계 A에서 벡터 v가 위 같이 정의되어 있다고 해보자.
이제 또다른 좌표계 B를 살펴보자.

좌표계 B 입장에선 A는 임의만큼 회전된 좌표계로 보일 것이다.
벡터는 위치에 대한 정보를 가지지 않으므로 위치의 차이는 중요하지 않다.
그러므로 좌표계 B입장에서 좌표계 A의 벡터 v를 해석하기 위해서는
vA 벡터를 좌표계 A가 회전된 만큼 회전시켜줘야한다.
회전 시키는 방법은 벡터의 선형결합을 활용한다.
이 때 사용하는 기저 벡터는 좌표계 B 입장에서의 바라본 좌표계 A의 기저 벡터들이다.
좌표계 B 입장에서 바라본 좌표계 A의 기저 벡터를 각각 e1, e2라고 해보자.
그러면 벡터 vB는 다음과 같다.

이 식이 의미하는 것은
vA 벡터를 B 좌표계 입장에서 해석한 것이다.
시각적으로 나타내면 이와 같다.
점 변환
점 변환의 경우는 식이 조금 달라진다.
점은 위치또한 중요하기 때문이다.
먼저, 벡터 vA를 회전시켜서 좌표계 B를 기준으로 새로운 점을 생성한다
그 다음, 원래 pA는 좌표계 A의 원점으로부터 생성된 점이기에..
좌표계 A의 원점만큼 평행이동시켜주면 정확한 B입장에서 바라보는 점 A의 좌표를 얻어낼 수 있을 것이다.
시각적으로 나타내면 위 그림과 같고
식은 위와 같다.
여기서
pb는 pa를 B 좌표계에서 재해석 한 점
ub, vb 는 A좌표계의 기저 벡터를 B 좌표계를 기준으로 나타낸 것
Qb는 B 좌표계의 원점으로부터 좌표계 A의 원점 사이의 벡터가 되겠다.
행렬 곱으로 나타내기
벡터 좌표계변환 식과, 점 좌표계 변환 식을 다시 보자.
이 두 식의 차이점은, 평행이동의 유무이다.
그러므로, 만약 0과 1만을 가질 수 있는 w라는 요소를 추가한다면 어떻게 될까?
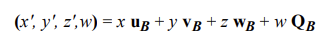
바로, 벡터 좌표계 변환과 점 좌표계 변환을 하나의 식으로 나타낼 수 있게 된다.
또, 이 식은 행렬곱으로 나타낼 수 있는데,
잘 보면 벡터 (x, y, z, w) 와 u, v, w, Q를 각각 행벡터로 꽂아 넣은 4x4 행렬의 곱셈으로 식을 변환할 수 있다.
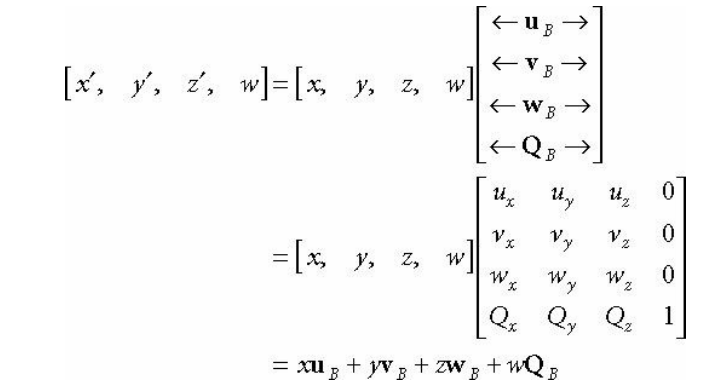
이 식은 아핀 변환식과 동일하다.
그러므로 아핀 변환을 좌표계 변환으로 해석할 수도 있고
좌표계 변환을 아핀 변환으로 해석할 수 있게 된다.
'컴퓨터 그래픽스 > 수학' 카테고리의 다른 글
| 컨벡스 결합에 대한 삽질 (0) | 2024.08.09 |
|---|---|
| [수학] 사원수: 4차원 수로 설계한 3차원 회전 (2) | 2024.07.30 |
| [수학] 오일러 공식 증명 (Euler's Formula) (0) | 2024.07.27 |
| [수학] 오일러 공식: 허수로 표현하는 회전 변환 (0) | 2024.07.25 |
| [수학] 복소수: 2차원 평면의 수 (6) | 2024.07.24 |





