개발하는 리프터 꽃게맨입니다.
[C++/이론] 최소 스패닝 트리 : 프림 알고리듬 (Prim Algorithm) 본문
스패닝 트리

임의의 그래프가 있다고 생각해봅시다.
스패닝 트리란 부분 그래프 중 하나로 다음과 같은 조건을 만족해야 합니다.
1) 그래프 내의 모든 정점을 포함하는 부분 그래프
2) 사이클이 없는 그래프
이런 그래프를 신장 트리 (혹은 스패닝 트리)라고 합니다.

스패닝 트리를 찾는 것은 매우 단순합니다.
단순 BFS, DFS를 하면 스패닝 트리를 찾을 수 있죠.
그런데 가중치 그래프의 경우를 생각해봅시다.
모든 노드를 다 방문하는데 비용이 다 다르다면,
아무래도 최소 비용으로 방문하는 것이 가장 좋겠죠?
그래서 중요하게 다뤄지는 알고리즘이 최소 신장 트리 (최소 스패닝 트리) 이며,
이는 모든 노드를 방문하는 최소 비용의 신장트리를 찾는 것을 목적으로 합니다.
최소 비용 경로 알고리즘과 무엇이 다른가요?
최소 비용 경로는 특정 노드에서 출발해 다른 노드로 도착하는 최소 비용 경로를 구합니다.
그러나 최소 신장 트리 알고리즘은 모든 노드를 다 방문하는 최소 비용의 부분 그래프를 찾는 것을 목적으로 합니다.
최소 비용 경로 알고리즘은 출발점에서 다른 모든 노드로 최단 경로로 도착하는 것이 목적이고
최소 신장 트리 알고리즘은 모든 정점을 방문하는 최소 비용의 트리를 찾는 것이 목적입니다.
프림 알고리즘
1) 개요
최소 신장 트리 구현에 사용되는 알고리즘은 특정 한 지점에서 출발하여 이 때까지 발견한 간선중 항상 최소의 간선만 발견해서 탐색해나가는 그리디 알고리즘을 바탕으로한 알고리즘입니다.
그래프에서 사이클을 만들면 안되기 때문에 방문한 노드는 다시 방문하지 않습니다.
2) 동작

1. 시작 노드를 하나 정해서, 0의 비용으로 우선순위 큐에 넣어둡니다.
이 때, 우선순위 큐는 비용에 대해서 최소 힙을 구성합니다.
2. 우선순위 큐에서 경로 정보를 하나 빼되, 이미 방문한 노드라면 스킵합니다.
3. 주변 경로를 탐색해서 우선순위큐에 다 넣어둡니다.
4. 우선 순위 큐가 빌 때까지 반복합니다.
3) 구현
위 소개한 그림을 기준으로 알고리즘을 작성해보겠습니다.
기본 구조입니다.
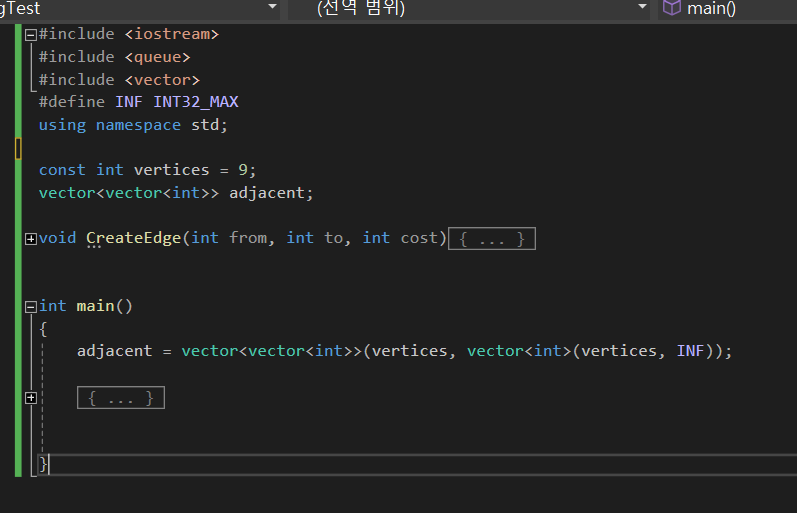
인접 행렬로 구현했고,
CreateEdge 는 노드를 연결하는 부분인데 딱히 중요한 부분은 아닙니다.
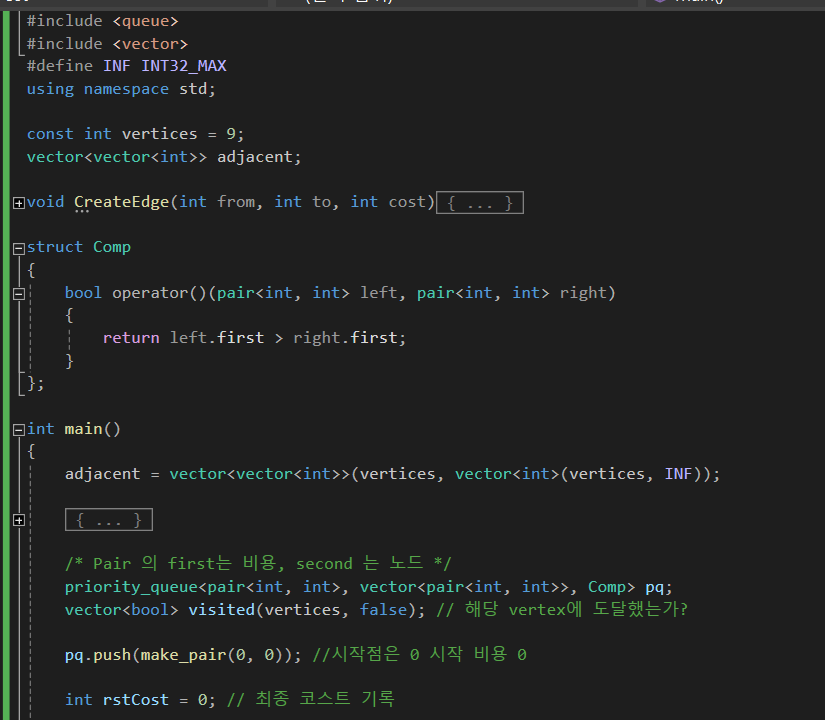
비용 기준으로 최소 힙을 이루는 pq를 선언하고,
사이클을 방지하기 위해 방문한 노드를 기록할 visited 를 선언합니다.
그리고 pq에 시작점을 넣어서 최소 스패닝 트리를 찾기 시작합니다.
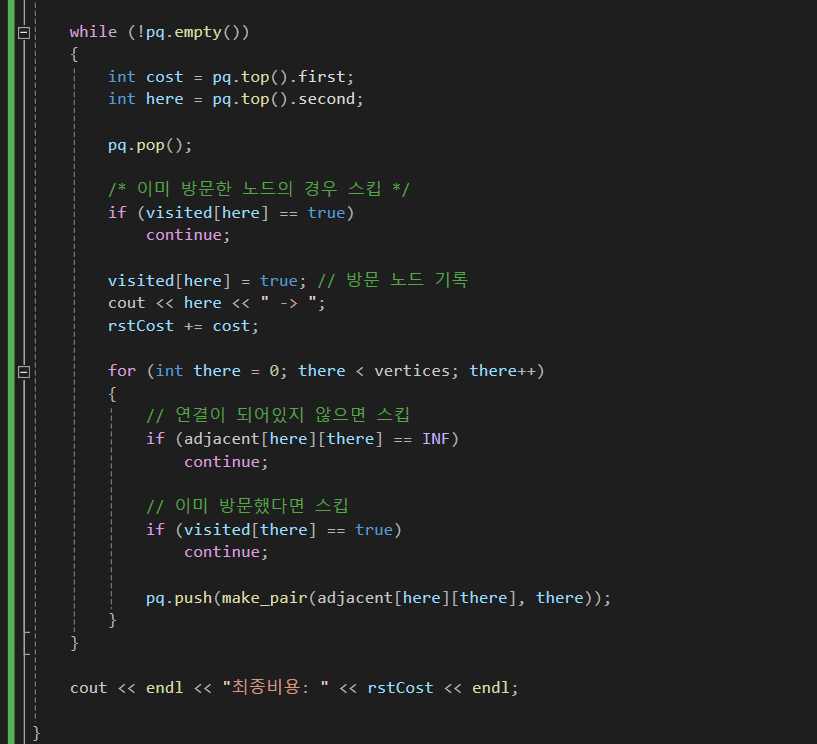
pq의 top부분에는 항상 가작 저렴한 경로가 존재합니다.
그렇기에 top에 있는 경로를 빼서,
만약 방문한 노드라면 (최소 비용이 이미 결정되었다는 의미) 스킵하고
아니라면 방문합니다.
그리고 그 노드를 기준으로 연결된 노드들을 확인합니다.
그리고 pq에 연결된 주변 노드 정보를 삽입하는데,
만약 비용이 저렴하다면 pq의 특성상 top으로 떠오르게 됩니다.
4) 시간 복잡도
우선순위 큐를 사용하는 프림 알고리즘의 시간 복잡도는
O((V+E) log V) 입니다.
V는 정점의 수, E는 간선의 수인데
각 정점은 우선순위 큐에 삽입되으로 VlogV 가 소모되며
간선의 수만큼 우선순위 큐에서 삭제 및 갱신이 일어나므로 2E log V 가 소모됩니다.
프림 알고리즘과 유사하게 스패닝 트리를 찾는 알고리즘은 크루스칼 알고리즘인데
이 친구는 복잡도가 O(E log E) 입니다.
즉, 밀집 그래프에서는 프림 알고리즘이 크루스칼 알고리즘보다 더 효율적일 수 있습니다.
5) 전체 코드
#include <iostream>
#include <queue>
#include <vector>
#define INF INT32_MAX
using namespace std;
const int vertices = 9;
vector<vector<int>> adjacent;
void CreateEdge(int from, int to, int cost)
{
adjacent[from][to] = cost;
adjacent[to][from] = cost;
}
struct Comp
{
bool operator()(pair<int, int> left, pair<int, int> right)
{
return left.first > right.first;
}
};
int main()
{
adjacent = vector<vector<int>>(vertices, vector<int>(vertices, INF));
{
CreateEdge(0, 1, 4);
CreateEdge(0, 7, 8);
CreateEdge(1, 7, 11);
CreateEdge(1, 2, 8);
CreateEdge(2, 8, 2);
CreateEdge(2, 5, 4);
CreateEdge(2, 3, 7);
CreateEdge(3, 5, 14);
CreateEdge(3, 4, 9);
CreateEdge(4, 5, 10);
CreateEdge(5, 6, 2);
CreateEdge(6, 7, 1);
CreateEdge(6, 8, 6);
CreateEdge(8, 7, 7);
}
/* Pair 의 first는 비용, second 는 노드 */
priority_queue<pair<int, int>, vector<pair<int, int>>, Comp> pq;
vector<bool> visited(vertices, false); // 해당 vertex에 도달했는가?
pq.push(make_pair(0, 0)); //시작점은 0 시작 비용 0
int rstCost = 0; // 최종 코스트 기록
while (!pq.empty())
{
int cost = pq.top().first;
int here = pq.top().second;
pq.pop();
/* 이미 방문한 노드의 경우 스킵 */
if (visited[here] == true)
continue;
visited[here] = true; // 방문 노드 기록
cout << here << " -> ";
rstCost += cost;
for (int there = 0; there < vertices; there++)
{
// 연결이 되어있지 않으면 스킵
if (adjacent[here][there] == INF)
continue;
// 이미 방문했다면 스킵
if (visited[there] == true)
continue;
pq.push(make_pair(adjacent[here][there], there));
}
}
cout << endl << "최종비용: " << rstCost << endl;
}'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [C++/알고리즘] 이진탐색 (0) | 2024.03.21 |
|---|---|
| [C++/이론] 최소 스패닝 트리 : 크루스칼 알고리듬 (Kruskal Algorithm) (2) | 2024.02.14 |
| [C++] 15903번. 카드 합체 놀이 (2) | 2024.01.31 |
| [C++] A* 알고리즘을 이용한 '미로찾기 알고리즘' (1) | 2024.01.06 |
| [C++/이론] 다익스트라 알고리즘 (Dijkstra Algorithm) (1) | 2024.01.04 |




