참고: https://powerclabman.tistory.com/24
참고: https://powerclabman.tistory.com/25
가중치 그래프

이전 포스팅에서 사용했던 그래프는 모두 가중치가 없는 그래프였습니다.
즉, 노드와 노드를 이동하는데 비용이 동일하다는 것이죠.
근데, 실제로 상황에서 A->B로 가는 것과 A->C로 가는 것의 비용이 다를 수도 있겠죠?
서울 -> 강원도
서울 -> 부산
두 조건 다 도시와 도시 사이를 이동하는 것이지만,
소모하는 기름, 거리, 톨게이트 비용 등..
많은 것이 다를 것입니다.
이런 비용을 '가중치' 라고 하고,
가중치를 표현한 그래프를 '가중치 그래프'라고 부릅니다.
int adjacent[5][5] =
{
0,1,1,0,0,
0,0,1,0,1,
0,0,0,1,0,
0,0,0,0,1,
0,0,0,0,0
};인접 행렬 그래프를 이렇게 표현하곤 했었는데요
int adjacent[5][5] =
{
0,2,1,0,0,
0,0,3,0,4,
0,0,0,4,0,
0,0,0,0,8,
0,0,0,0,0
};이런 식으로, 연결에 cost (혹은 weight) 를 부여하여
가중치를 표현할 수 있습니다.

가중치 그래프와 관련된 상당히 많은 문제들이 있습니다.
1) 최소 비용 신장 트리 (Minimum Spanning Tree)
모든 노드를 연결하는 부분 그래프를 '신장 트리'라고 하는데,
가중치 합이 최소가 되는 '신장 트리'를 찾고자하는 알고리즘
2) 최단 경로 문제 (Shortest Path)
하나의 시작 노드로 부터 모든 다른 정점까지의 최단 경로를 찾는 알고리즘
오늘은 가중치 그래프의 '최단 경로 문제'를 해결하는 알고리즘인
'다익스트라 알고리즘'을 소개해보도록 하겠습니다.
다익스트라 알고리즘
1. 개요
먼저 임의의 그래프를 정의해봅시다.

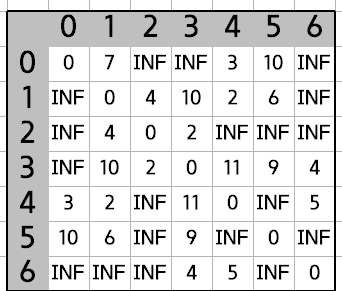
가중치 그래프는 인접 행렬 혹은 인접 리스트로 정의할 수 있고
자기 자신은 0, 연결된 노드는 고유의 가중치(Cost)
그리고 연결되지 않은 노드는 INF로 표시합니다.
INF는 가중치가 무한하다는 의미로, INF로 설정 시 연결되지 않음을 나타냅니다.
다익스트라 알고리즘의 논리 과정은 다음 의사코드를 보고 설명해 드리겠습니다.
2. 의사코드
visited 배열은 '해당 노드에 방문했는지?'를 bool 형으로 판단한다.
distance 배열은 '출발 노드에서 도착 노드까지의 최소 비용'을 저장한다.
distance[u] 는 v->u의 최소 비용이라는 의미
distance 배열은 초기에 충분히 큰 값으로 초기화된다.
Dijkstra(시작정점) :
distance[시작점] <- 0
while(모든 정점을 모두 방문할 때 까지)
for(방문하지 않은 정점중 distance 값이 가장 작은 정점 탐색)
그러한 정점을 here 라고 함
visited[here] <- true
for(연결된 모든 노드를 탐색한다.)
distance[u] = min(distance[u], distance[here] + adjacent[here][u])
다익스트라 알고리즘에서 가장 중요한 것은
시작 정점을 v라고 하고, 임의의 정점을 u라고 할 때
v -> u의 최소비용을 저장하고 있는
distance에 대한 이해입니다.

distance는 초기에 INF로 초기화됩니다.
distance [0]은 출발점이니, 0을 대입해 줍니다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | INF | INF | INF | INF | INF | INF |
이제, 방문하지 않은 노드 중에서 distance [here]가 최소인 노드를 찾아줍니다.
위 예시에서는 노드 0이겠죠
그리고, 노드 0과 연결된 모든 노드의 가중치를 관찰합니다.
0->1 : 7
0->4 : 3
0->5 : 10
이네요.
그리고
distance [u] = min(distance [u], distance [here] + adjacent [here][u]
연산을 수행해 주는데, 이것이 의미하는 바는 다음과 같습니다.
1) distance [here]은 '출발점->here' 의 명백한 최소 거리이다.
2) distance[here] + adjacent [here][u]는 최소 거리가 될 가능성이 있다.
3) distance [u]의 값과 distance [here] + adjacent [here][u]를 비교해서 둘 중 최소의 값을 대입한다.
라고 이해할 수 있습니다.
| 0(방문) | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 7 | INF | INF | 3 | 10 | INF |
그럼 이런 식으로 업데이트되겠죠,
그리고, 0은 이미 방문했으니까 visited [0]을 true로 체크하는 걸 잊으면 안 됩니다.
| 0(방문) | 1 | 2 | 3 | 4(방문) | 5 | 6 |
| 0 | 7 | INF | 14 | 3 | 10 | 8 |
이것을 계속 반복합니다.
| 0(방문) | 1(방문) | 2 | 3 | 4(방문) | 5 | 6 |
| 0 | 5 | INF | 14 | 3 | 10 | 8 |
방문된 distance [idx]의 값이 이미 명백하게 최소 거리입니다.
| 0(방문) | 1(방문) | 2 | 3 | 4(방문) | 5 | 6(방문) |
| 0 | 5 | 9 | 12 | 3 | 10 | 8 |
| 0(방문) | 1(방문) | 2(방문) | 3 | 4(방문) | 5 | 6(방문) |
| 0 | 5 | 9 | 11 | 3 | 10 | 8 |
| 0(방문) | 1(방문) | 2(방문) | 3 | 4(방문) | 5(방문) | 6(방문) |
| 0 | 5 | 9 | 11 | 3 | 10 | 8 |
| 0(방문) | 1(방문) | 2(방문) | 3(방문) | 4(방문) | 5(방문) | 6(방문) |
| 0 | 5 | 9 | 11 | 3 | 10 | 8 |
이렇게 모든 노드를 방문하면 알고리즘이 종료됩니다.
아마 BFS, DFS 알고리즘보다 조금 어려운 감이 있을 수도 있나
다음과 같은 논리 과정을 되새기면 감이 조금 잡힙니다.
1. distance에서 방문하지 않은 노드 중 최소 값을 찾아서
2. 최소 값인 노드를 방문하고
3. distance 값을 업데이트해준다.
4. (반복)
3. 최종코드
void Dijkstra(Graph& g, int start)
{
vector<bool> visited(g._vertex, false);
vector<int> distance(g._vertex, INF); //충분히 큰 수 INT = 9999 정도로 설정
distance[start] = 0;
while (true)
{
int here = -1;
int minCost = INF;
for (int v = 0; v < g._vertex; v++)
{
//이미 방문한 노드면 스킵
if (visited[v] == true)
continue;
//방문하지않은 노드중에 최소 가중치 노드 찾기
if (minCost > distance[v])
{
here = v;
minCost = distance[v];
}
}
//모든 노드를 다 방문했으면 탈출
if (here == -1)
break;
//here 노드를 방문
visited[here] = true;
//연결된 노드들의 가중치 관찰 및 갱신
for (int there = 0; there < g._vertex; there++)
distance[there] = min(distance[there], minCost + g._adjacent[here][there]);
}
//이건 출력 코드
for (int i = 0; i < g._vertex; i++)
cout << "[" << i << "]: " << distance[i] << endl;
}
<전체 코드>
#include <iostream>
#include <vector>
#define INF 9999
using namespace std;
class Graph
{
public:
Graph(int v)
: _vertex(v)
{
_adjacent = vector<vector<int>>(_vertex, vector<int>(_vertex, INF));
}
void CreateEdge(int from, int to, int cost)
{
//무방향 그래프임을 가정
_adjacent[from][to] = cost;
_adjacent[to][from] = cost;
}
public:
int _vertex;
vector<vector<int>> _adjacent;
};
void Dijkstra(Graph& g, int start)
{
vector<bool> visited(g._vertex, false);
vector<int> distance(g._vertex, INF);
distance[start] = 0;
while (true)
{
int here = -1;
int minCost = INF;
for (int v = 0; v < g._vertex; v++)
{
//이미 방문한 노드면 스킵
if (visited[v] == true)
continue;
//방문하지않은 노드중에 최소 가중치 노드 찾기
if (minCost > distance[v])
{
here = v;
minCost = distance[v];
}
}
//모든 노드를 다 방문했으면 탈출
if (here == -1)
break;
//here 노드를 방문
visited[here] = true;
//연결된 노드들의 가중치 관찰
for (int there = 0; there < g._vertex; there++)
distance[there] = min(distance[there], minCost + g._adjacent[here][there]);
}
for (int i = 0; i < g._vertex; i++)
cout << "[" << i << "]: " << distance[i] << endl;
}
int main()
{
Graph g(7);
//그래프 정의
{
g.CreateEdge(0, 1, 7);
g.CreateEdge(0, 4, 3);
g.CreateEdge(0, 5, 10);
g.CreateEdge(1, 4, 2);
g.CreateEdge(1, 2, 4);
g.CreateEdge(1, 5, 6);
g.CreateEdge(1, 3, 10);
g.CreateEdge(2, 3, 2);
g.CreateEdge(4, 6, 5);
g.CreateEdge(3, 6, 4);
g.CreateEdge(3, 5, 9);
g.CreateEdge(3, 4, 11);
}
Dijkstra(g, 0);
}
다익스트라 알고리즘은 n개의 정점이 있는 그래프가 있다고 하면
n개의 정점을 방문하고, 다른 n개의 정점의 '가중치'를 관찰하기에
O(n^2)의 복잡도를 가집니다.
다익스트라 알고리즘 우선순위 큐 최적화
1. 개요
우선순위 큐를 이용하면, E를 간선, V를 노드라고 했을 때
다익스트라 알고리즘의 시간복잡도를 O(E log V)까지 줄일 수 있습니다.
그럼 우선순위 큐로 어떻게 다익스트라 알고리즘을 구현하는지 설명해 보도록 하겠습니다.
겉모습은 BFS 알고리즘과 유사합니다.
2. 의사 코드
<가중치, 노드> 짝을 저장하는 '최소 힙' 우선순위 큐 pq를 정의합니다.
distance 에는 앞서 설명했던 것과 마찬가지로 출발점 v부터 u 까지의 최소 거리를 저장합니다.
Dijkstra_PQ(시작정점) :
distance[시작정점] = 0;
pq 에 <가중치, 노드> 짝 삽입
while(pq 가 빌 때 까지)
pq를 후보를 pop
if(만약 후보가 distance[u] 보다 좋은 선택지가 아니라면)
스킵
for(다른 정점들을 순회한다.)
if(distance[u]가 후보 + adjacent[here][u]보다 클 경우)
distance[u]를 갱신하고
pq에 <가중치, 노드>를 push 한다.
굉장히 코드가 간단해졌습니다.
최적화 전 코드와 비교해 보면
1) 최소 값을 찾는 부분이 없어졌습니다.
2) 방문 노드를 관리하지 않습니다.
라는 특징이 있습니다.
1) 최소 값을 찾는 부분은 '우선순위 큐'가 제 역할을 충분히 해주고 있기 때문입니다.
pq에 <가중치, 노드>를 넣으면, 항상 distance [u]를 갱신한 <가중치, 노드> 짝 중
가중치가 가장 작은 값을 짧은 시간에 뽑아 쓸 수 있습니다.
2) 첫 번째 방법은 최소 distance를 찾기 위해 모든 distance를 탐색해야만 하기에,
방문한 노드의 경우 visited로 체크해 주어 중복 방문을 하지 않도록 해줘야만 합니다.
그런데, 우선순위 큐는 항상 가장 작은 노드를 추출하기에, 굳이 distance를 탐색할 필요가 없고
자연스럽게 visited도 사용할 필요가 없어집니다.
3. 전체 코드
void Dijkstra_PQ(Graph& g, int start)
{
priority_queue<pair<int, int>> pq;
vector<int> distance(g._vertex, INF);
distance[start] = 0;
pq.push(make_pair(0, start));
while (!pq.empty())
{
int here = pq.top().second;
int hereCost = pq.top().first;
pq.pop();
//예외처리
if (hereCost > distance[here])
continue;
for (int there = 0; there < g._vertex; there++)
{
int cost = hereCost + g._adjacent[here][there];
if (distance[there] > cost)
{
distance[there] = cost;
pq.push(make_pair(distance[there], there));
}
}
}
for (int i = 0; i < g._vertex; i++)
cout << "[" << i << "] : " << distance[i] << endl;
}
<전체 코드>
#include <iostream>
#include <vector>
#include <queue>
#define INF 9999
using namespace std;
class Graph
{
public:
Graph(int v)
: _vertex(v)
{
_adjacent = vector<vector<int>>(_vertex, vector<int>(_vertex, INF));
}
void CreateEdge(int from, int to, int cost)
{
//무방향 그래프임을 가정
_adjacent[from][to] = cost;
_adjacent[to][from] = cost;
}
public:
int _vertex;
vector<vector<int>> _adjacent;
};
void Dijkstra_PQ(Graph& g, int start)
{
priority_queue<pair<int, int>> pq;
vector<int> distance(g._vertex, INF);
distance[start] = 0;
pq.push(make_pair(0, start));
while (!pq.empty())
{
int here = pq.top().second;
int hereCost = pq.top().first;
pq.pop();
//예외처리
if (hereCost > distance[here])
continue;
for (int there = 0; there < g._vertex; there++)
{
int cost = hereCost + g._adjacent[here][there];
if (distance[there] > cost)
{
distance[there] = cost;
pq.push(make_pair(distance[there], there));
}
}
}
for (int i = 0; i < g._vertex; i++)
cout << "[" << i << "] : " << distance[i] << endl;
}
int main()
{
Graph g(7);
//그래프 정의
{
g.CreateEdge(0, 1, 7);
g.CreateEdge(0, 4, 3);
g.CreateEdge(0, 5, 10);
g.CreateEdge(1, 4, 2);
g.CreateEdge(1, 2, 4);
g.CreateEdge(1, 5, 6);
g.CreateEdge(1, 3, 10);
g.CreateEdge(2, 3, 2);
g.CreateEdge(4, 6, 5);
g.CreateEdge(3, 6, 4);
g.CreateEdge(3, 5, 9);
g.CreateEdge(3, 4, 11);
}
Dijkstra_PQ(g, 0);
}
마치며
이 알고리즘은 매우 실용적인 알고리즘으로 적은 비용으로 가장 빠르게 해답에 도달하는 경로를 찾아내는 대부분의 문제에 응용됩니다.
이런 최소 경로 문제는 현실세계에 매우 빈번하므로 실질적 이용의 예시는 수도 없이 많겠죠.
그만큼 유용하고 활용가능성이 높은 알고리즘입니다.
루빅스 큐브, 내비게이션, 라우팅 알고리즘 등.. 수많은 분야에서 실용적이게 사용할 수 있습니다
이전 포스팅에서 '미로 찾기 알고리즘'에 대해서 다뤘는데요,
다익스트라를 이용하면 미로찾기 또한 효율적이게 해결할 수 있습니다.
최소경로를 구하는 것이 다익스트라 알고리즘의 역할이니까요!
그런데, 그냥 쌩 '다익스트라 알고리즘'을 적용해서는 해결하지 못합니다.
결국 다익스트라 알고리즘도 전체 미로를 다 탐색한 뒤 최소 경로를 찾아내는 알고리즘이기 때문이죠.
즉, 다익스트라 역시 BFS 알고리즘의 단점인 '계산 오버헤드' 문제를 피할 수 없습니다.
그러면 다익스트라 알고리즘을 '미로찾기 알고리즘'으로 사용하기 위한 방법은 무엇일까요?
그것은 다음 포스팅에서 'A* 알고리즘'을 소개하면서 다뤄보겠습니다.
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [C++] 15903번. 카드 합체 놀이 (2) | 2024.01.31 |
|---|---|
| [C++] A* 알고리즘을 이용한 '미로찾기 알고리즘' (1) | 2024.01.06 |
| [C++] 경로 역추적: BFS을 이용한 '미로찾기 알고리즘' (2) | 2024.01.04 |
| [C++] 깊이 우선 탐색과 너비 우선 탐색 (BFS/DFS) (0) | 2024.01.04 |
| [C++/이론] 그래프 개론 (1) | 2024.01.04 |