개발하는 리프터 꽃게맨입니다.
[C++/이론] 최소 스패닝 트리 : 크루스칼 알고리듬 (Kruskal Algorithm) 본문
https://powerclabman.tistory.com/90
[C++/이론] 최소 스패닝 트리 : 프림 알고리듬 (Prim Algorithm)
스패닝 트리 임의의 그래프가 있다고 생각해봅시다. 스패닝 트리란 부분 그래프 중 하나로 다음과 같은 조건을 만족해야 합니다. 1) 그래프 내의 모든 정점을 포함하는 부분 그래프 2) 사이클이
powerclabman.tistory.com
개요
크루스칼 알고리즘은 최소 스패닝 트리를 구하기 위한 또 다른 알고리즘입니다.
앞전에 소개한 프림 알고리즘과 차이점은,
프림 알고리즘의 경우 특정 노드에서 출발해 노드들을 탐색하면서 최소 스패닝 트리를 완성시켜나가는 알고리즘이었다면
크루스칼 알고리즘은 모든 경로를 두고, 최소 경로만 쏙쏙 선택해서 트리를 만들어낸다고 보면 되겠습니다.
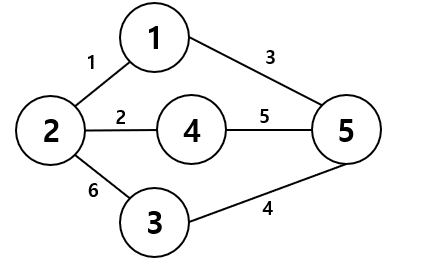
이런 식으로 경로에 대한 정보를 알고 있다고 가정하고
작은 순으로 경로를 뽑아보자면
1, 2, 3, 4 의 경로만 뽑아서 만들면 되겠네요.
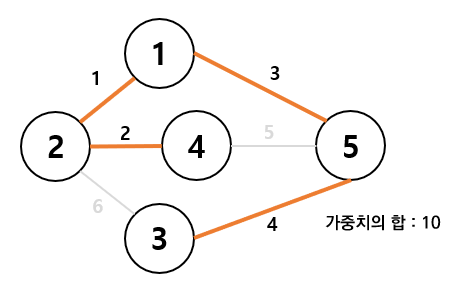
이런 식으로 말이죠.
이것도 그리디 알고리즘과 같은 발상입니다.
그런데 주의해야할 것이 있습니다.
바로 사이클 문제입니다.

이런 그래프가 있다고 생각해봅시다.
경로들의 cost를 기준으로 오름차순 정렬을 하면,
[2,4] 3
[1,4] 4
[2,3] 5
[1,2] 6
[2,5] 7
이런 식으로 되겠죠?
그리고 [2, 4] [1, 4] [2, 3] [1, 2] 를 선택해봅시다.
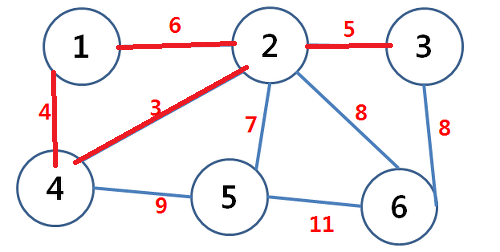
사이클이 생겨버립니다.
신장트리의 조건 중 하나가 사이클이 있으면 안된다는 것이였죠?
그러므로
무작정 작은 경로를 선택해서는 안되고, 사이클이 생기지 않는 범위에서 경로를 선택하는 것이
크루스칼 알고리즘의 핵심입니다.
이를 해결하기 위해 유니온-파인드라는 알고리즘을 사용하게 되죠.
유니온-파인드
유니온 파인드는 서로 다른 2개의 노드가 같은 그래프에 속하는지 판별하는 알고리즘입니다.
만약, 다른 그래프라고 한다면, 2개의 그래프가 모두 서로 다른 노드를 가지고 있다는 의미가 되겠죠?
이러한 그래프 관계를 서로소 집합(Disjoint-Set)이라고 부릅니다.
간단하게 말하자면, 두 집합의 교집합이 공집합이 되는 관계에 있다라고 말할 수 있겠네요.
1) 개요
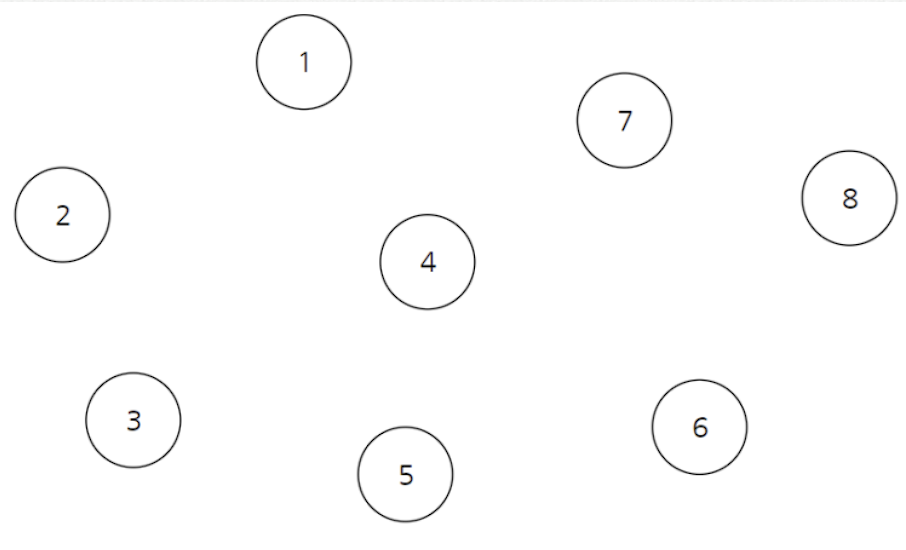
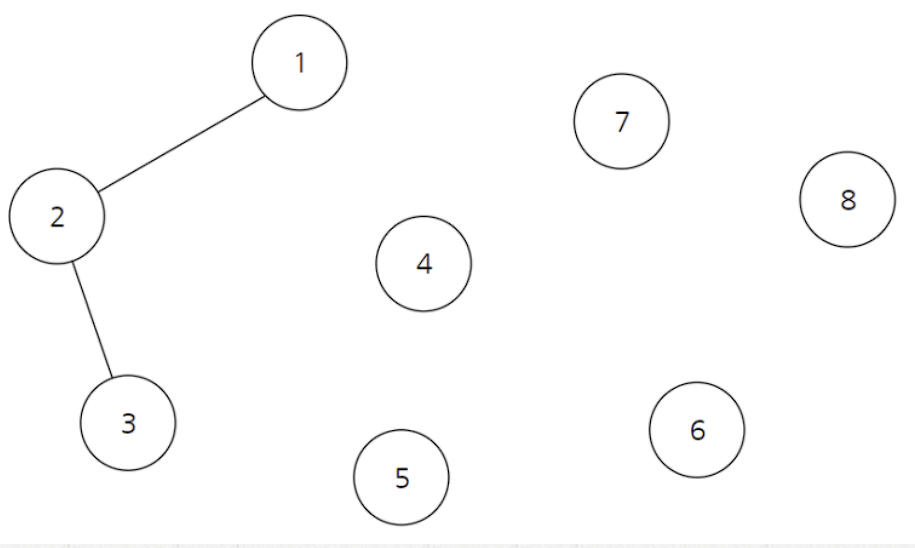
위와 같은 8개의 노드가 있다고 생각해봅시다.
유니온 파인드를 하기위해서는 Parent 라는 배열이 필요하며, Parent 배열에는 해당 노드의 부모 노드를 기록하고 있습니다. 부모 노드가 없을 경우 -1 로 표기합니다.


만약 이런식으로 관계가 바뀌었다면
parent 표는 다음과 같이 바꿀 수 있습니다.

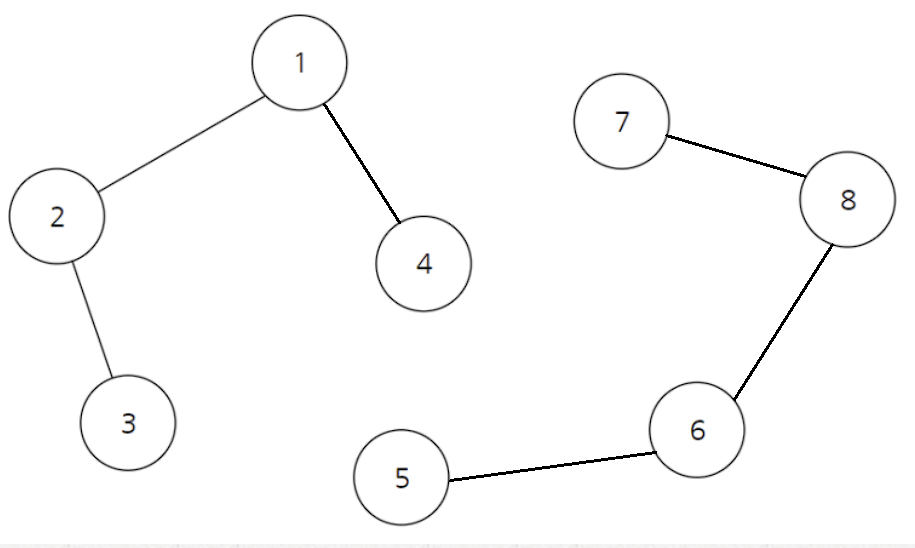
이제 이런 식으로 만들어 낸다면 표는 다음과 같아지겠죠.
이제 이 표를 이용해서 다른 두 노드에 대해 같은 그래프에 속하는지 판별할 수 있습니다.

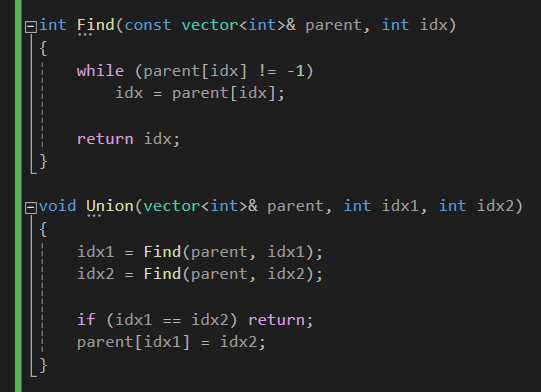
2) Find
만약, 노드 3과 6이 같은 그래프에 속하는지 알아봅시다.
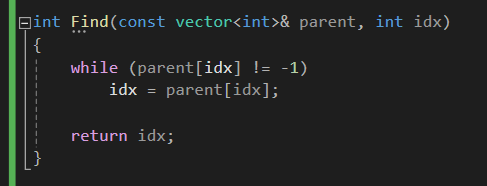
Find 함수는 위와 같습니다.
루트 노드 (부모가 없는 노드) 가 나올 때 까지 트리 계층을 쭉 올라가보는 것이죠.
만약에, 두 노드가 같은 그래프에 속해있다면, 리턴값은 같을 것이고
다른 그래프에 속해있다면 리턴값은 다를 것입니다.
말했던대로 노드 3과 6을 매개변수로 넘겼을 때 그 값은 각각
1과 7입니다.
즉, 두 노드는 다른 그래프에 있다는 것이죠.
3와 4를 비교해보면 그 둘의 결과값은 둘 다 1이므로
두 노드는 같은 그래프에 있다는 것이 됩니다.
3) Union
유니온 함수는 두 그래프를 합쳐주는 것을 뜻합니다.
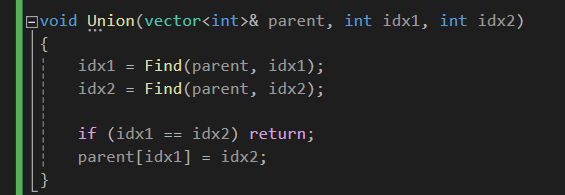
임의의 두 노드의 루트 노드를 찾아서,
이미 같은 그래프의 경우에는 넘기고
만약 두 노드가 다른 그래프에 존재했다면,
루트 노드끼리 연결해서 같은 그래프로 만들어버립니다.
이제 다음 목차에서 유니온-파인드를 통해, 사이클을 판단하고 최소 스패닝 트리를 만드는 것을 보여드리겠습니다.
크루스칼 알고리즘
1) 동작

1. 경로에 대한 정보를 나타내는 구조체를 만든다.
해당 구조체는 출발노드, 도착노드, 가중치가 담겨져있다.
2. 그래프에서 경로 정보를 뽑아낸다.
3. 경로를 가중치에대한 오름차순으로 정렬한다.
4. 경로를 하나씩 확인하면서 스패닝 트리를 완성한다.
단, 추가할 경로가 사이클은 만들어낸다면 스킵한다.
2) 구현
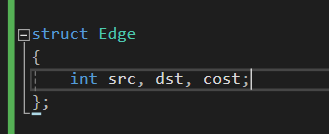
먼저 Edge 라는 구조체를 만들어서 그래프에서 경로정보를 다 빼오겠습니다.
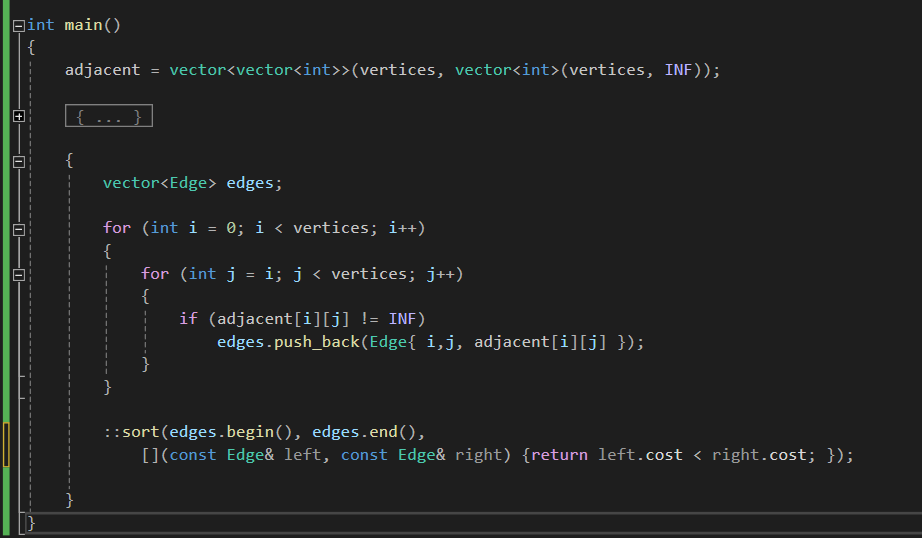
기존 제 코드는
adjacent 에 인접행렬 형식으로 연결 상태가 저장되어있었고,
이를 Edge 구조체 형태로 바꾸기 위해서 위와 같은 방식으로 빼왔습니다.
사실 이런 것은 어떤 방식으로 구현할 것인가에 따라서 달라지는 것이라고 생각하며,
가장 중요한 것은 sort 부분입니다.
가중치를 기준으로 오름차순 정렬을 해주는 것이죠.
이 때, 우선순위큐를 사용해도 상관없습니다.
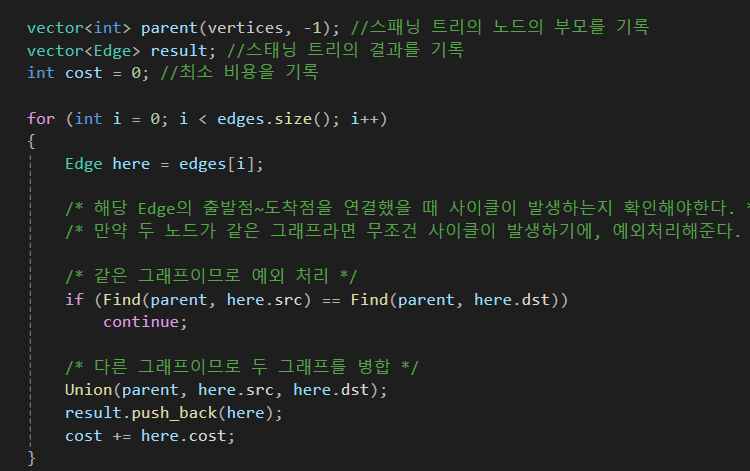
그리고 이것이 크루스칼 알고리즘의 메인 부분입니다.
그냥 최소 비용인 경로를 뽑아주고
이 경로를 연결했을 경우 사이클이 생기면 넘기고
아니면 Union을 이용해서 병합해줍니다.
상당히 단순한 구조를 가지고 있죠.
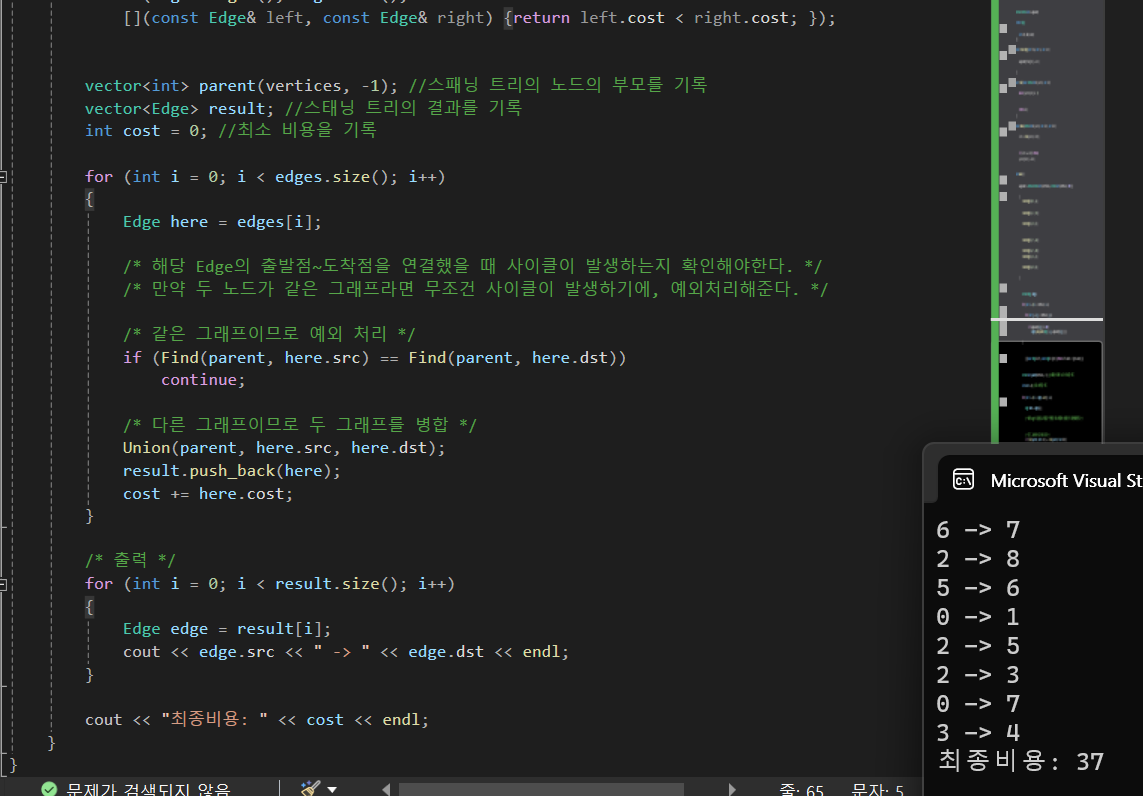
결과도 아주 잘 나옵니다.
3) 시간 복잡도
먼저 E 개의 간선에 대해서 정렬을 해야하니,
E log E 을 복잡도가 나올 것이고, E 개의 배열을 순회하니,
최종적으로 2E log E 의 복잡도가 나올 것이며
이는 O(E logE) 입니다.
만약, 간선의 개수가 매우 많은 밀집행렬의 경우 O(E logE)의 크루스칼 알고리즘보다는 프림을 사용하는 것이 나을 것이고, 희소 행렬일 경우 크루스칼 알고리즘이 더 나은 성능을 보일 것입니다.
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [C++/이론] Dijkstra 알고리즘의 한계점과 Bellman-Ford 알고리즘 (0) | 2024.05.19 |
|---|---|
| [C++/알고리즘] 이진탐색 (0) | 2024.03.21 |
| [C++/이론] 최소 스패닝 트리 : 프림 알고리듬 (Prim Algorithm) (0) | 2024.02.14 |
| [C++] 15903번. 카드 합체 놀이 (2) | 2024.01.31 |
| [C++] A* 알고리즘을 이용한 '미로찾기 알고리즘' (1) | 2024.01.06 |





