개발하는 리프터 꽃게맨입니다.
[수학] 절두체 : 최적화된 3차원 공간 본문
렌더링에 있어서 중한 것은 빠르게 그리는 것이고
가장 효과적인 방법은 시야에 보이는 물체만 그리는 것이다.
대표적인 기법으로는 백페이스 컬링을 들 수 있다.
그 외로 사용할 수 있는 기법을 알아보자.
절두체 컬링
개요
씬에 다수의 오브젝트가 있는 경우 모든 오브젝트를 그리는 것은 비효율적이고, 카메라 시야 안에 보이는 오브젝트만 그리는 것이 훨씬 효율적이다.
그래서 그래픽을 효율적이게 구현하기 위해선 시야, 절두체 영역에 속한 오브젝트만 그려내면 된다.
그렇다면 절두체 밖에 있는 오브젝트들을 걸러내야 하는데, 이러한 작업을 절두체 컬링 Frustum Culling 이라고 한다.

절두체는 6개의 면으로 이루어져 있다.
이 면들의 각각의 평면의 방정식을 구한 다음에 게임 오브젝트가 6개의 평면 중 하나라도 바깥쪽에 위치해 있다면 그리기에서 제외한다.
평면의 방정식

3차원 상의 평면의 방정식을 정의해보자.
3차원 상의 어떤 세 점은 반드시 평면을 만들어내기에 이를 이용해서 평면의 방정식을 만들수도 있지만
평면상의 한 점과 평면의 법선 벡터만 있어도 평면의 방정식을 만들기에는 충분하다.


평면의 벡터 n 과 평면위의 점 P0 가 주어졌다고 해보자.
편의상 법선 벡터 n은 정규화 벡터라 하자.
이 두 요소는 3차원 평면의 방정식을 정의하기 위해 최소한으로 필요한 정보다.
이와 같은 상황에서 임의의 점 P = (x, y, z) 를 정의해보자.
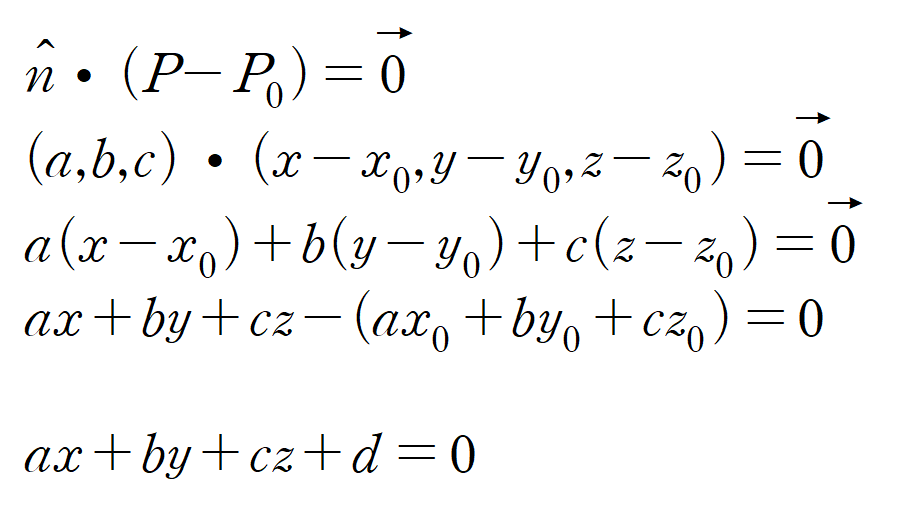
P-P0 가 만들어내는 벡터와 법선 벡터는 직교하기에 내적이 0이다. 이를 이용하면 위와같은 수식이 성립한다.
평면으로만 이뤄진 항은 어차피 상수이므로, 간단히 d로 바꿔도 무관하다.
그래서 마지막 줄에 있는 식이 최종적인 평면의 방정식이다.
여기서 상수 d가 가지는 의미를 생각해보자.
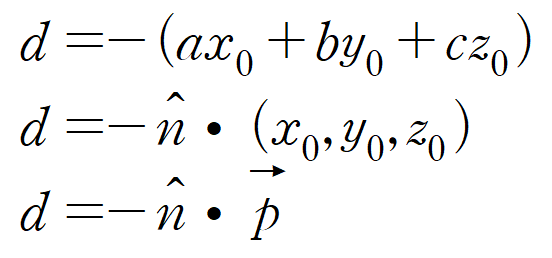
d는 복잡한 상수를 간단하게 바꾼 것이다.
그 복잡합 상수는 위 식의 첫 줄과 같다.
1행의 식은 내적을 통해 2행의 식으로 바꿀 수 있다.
앞서 평면의 방정식을 정의할 때, 평면 위 임의의 점 P를 사용했다.
점 P의 좌표는 벡터 OP와 같다.
그러므로 최종적으로 3행의 식을 얻어낼 수 있다.
두 벡터 n과 p를 시각화 하면 다음과 같다.
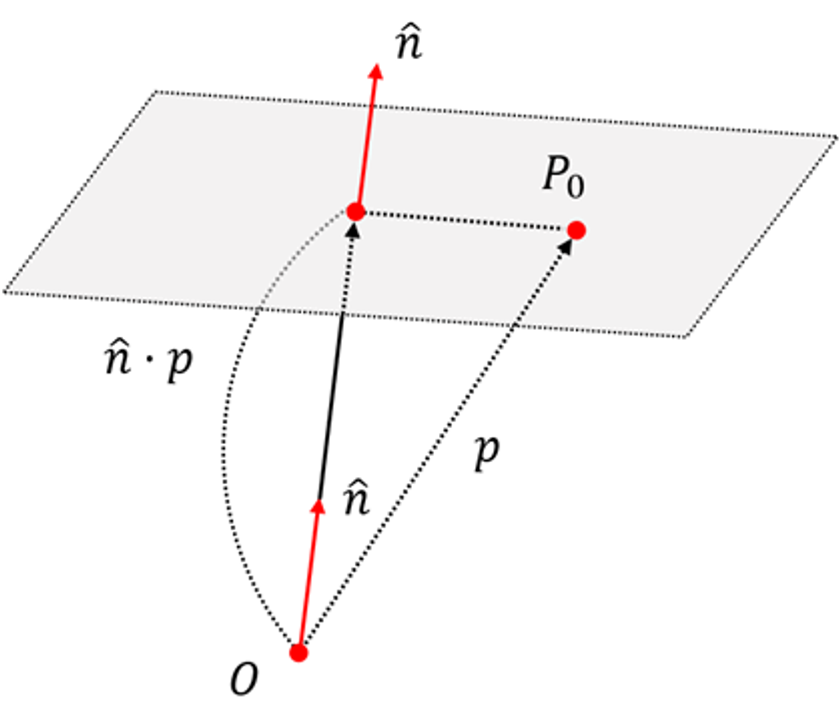
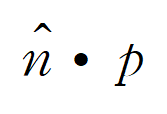
내적 np 에 대해서 살펴보자.
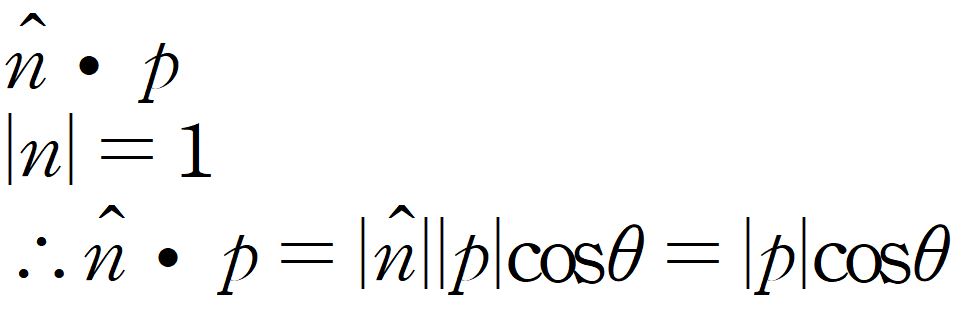
최종식 |p|cos 의 절댓값은 벡터 p를 벡터 n에 투영한 벡터의 크기를 의미한다.
평면과 법선 벡터n은 서로 직교하기 때문에 ||p| cos| 는 원점과 평면의 최단거리라고 여길 수 있다.
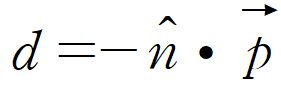
d의 식은 위와 같기 때문에
d로 알 수 있는 것은 2가지다.
1) 평면과 원점 사이 최단거리
2) 법선벡터의 방향 ( = 평면이 향하는 방향)
n과 p가 같은 방향일 경우, d는 음수이고
n과 p가 다른 방향일 경우, d는 양수이다.
1) 의 경우 d의 절댓값으로 판단한다.
2) 의 경우 d의 부호로 판별한다. d가 음수일 경우 평면은 원점에서 먼 곳을 바라보고 d가 양수일 경우 평면은 원점과 바라본다.
d의 정보는 평면의 방정식을 설계하는 데 큰 도움이 된다.
만약, 평면이 원점을 품는다면 어떻게 될까?
n과 p는 직교하기에 내적의 값이 0 나온다.
즉, 원점을 품는 평면의 방정식은 d = 0 이다.
이러한 평면은 ax + by + cz = 0 으로 정의할 수 있을 것이다.
응용 : 주어진 점이 평면의 안쪽에 있는지 판단하기
d 값을 응용하면 주어진 점이 평면의 안쪽에 있는지 바깥쪽에 있는지도 판별할 수 있다.
먼저, 3차원 공간의 어떤 점 P가 있다고 하자.
평면의 법선벡터 n과 벡터 OP를 내적한 값을 p라고 하자.
d + p > 0 일 경우 점 p 는 평면 바깥에 있다고 할 수 있다. 반대로
d + p < 0 일 경우 점 p 는 평면 안쪽에 있다고 할 수 있다.
이는 법선 벡터가 반대인 경우에도 동일하게 적용된다.
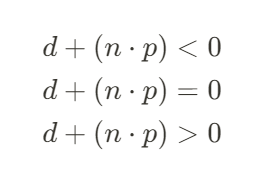
식은 간략하게 위와같이 나타낼 수 있다.
또, d 와 nㆍp 를 더한 값에 절댓값을 취하면, 평면에서 해당 점까지의 최단 거리를 구할 수 있다.
평면의 방정식 정규화
우리가 이 때까지 다뤘던 평면의 방정식은 법선벡터가 정규화 벡터였고 d 역시 정규화된 값이란걸 이해해야 한다.
임의의 평면의 방정식 ax + by + cz + d = 0 (a, b, c, d 는 실수) 이 주어진다고 해보자.
그러면 우리는 이 평면의 방정식을 정규화할 필요가 있다.
ax + by + cz + d = 0 이라는 평면의 방정식이 있을 때
법선벡터는 (a, b, c)이다. 이것을 정규화하면 다음과 같다.

그 다음 d를 보자.
d는 다음과 같이 구할 수 있다.
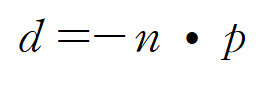
여기서 양변에 법선벡터의 크기를 나눈다면, 정규화된 d를 얻을 수 있을 것이다.
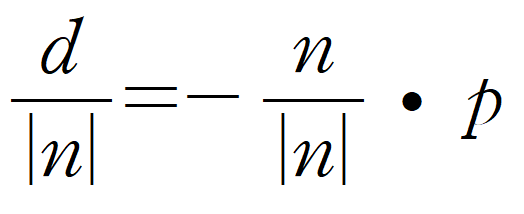
그럼 결국 평면의 방정식을 정규화하는 식은 다음과 같다.
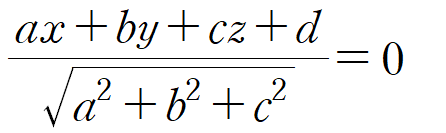
평면의 방정식을 활용한 절두체 표현
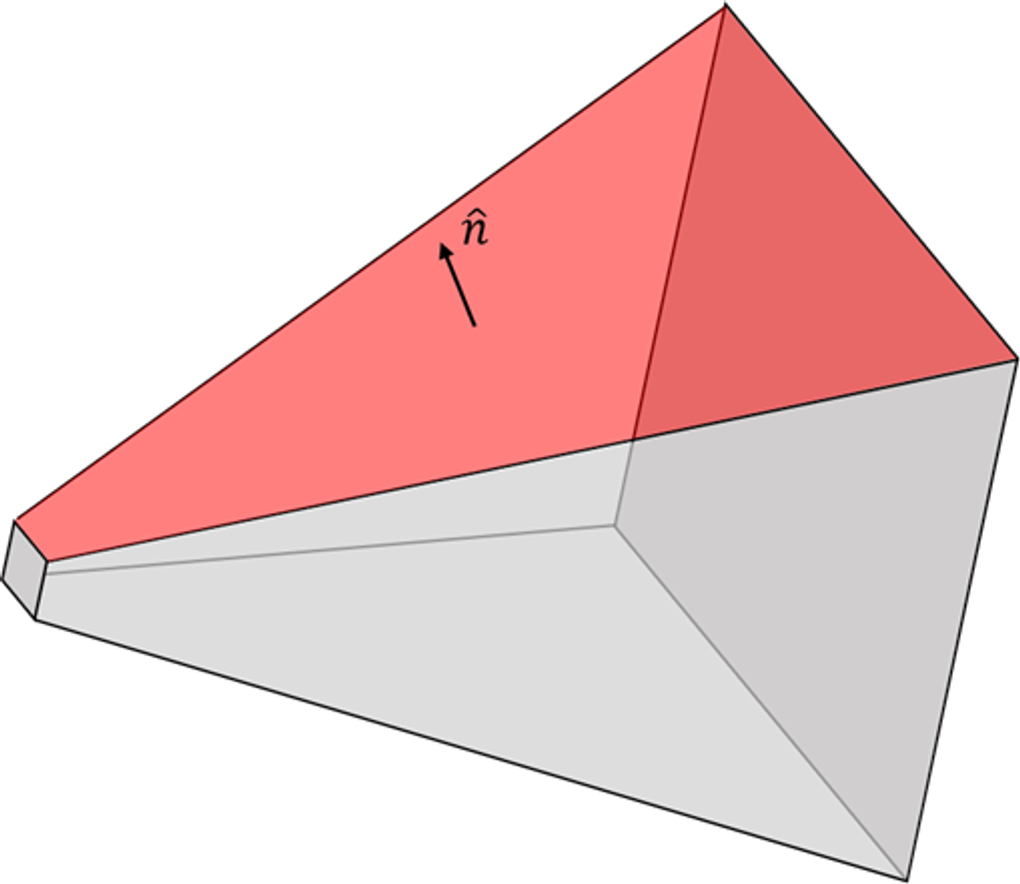
이제 절두체를 구성하는 6개의 평면에 대한 방정식을 직접 계산해보자.
먼저 절두체 상단 평면부터 살펴보자.
절두체 상당 평면을 무한히 확장하면 원점을 지나게 된다.
이러한 특성은 사실 근평면과 원평면을 제외한 나머지 평면에서도 동일하다.
그렇다면, 근평면과 원평면을 제외한 평면은 d값이 0이므로 법선 벡터만 구하면 방정식을 쉽게 얻을 수 있다.
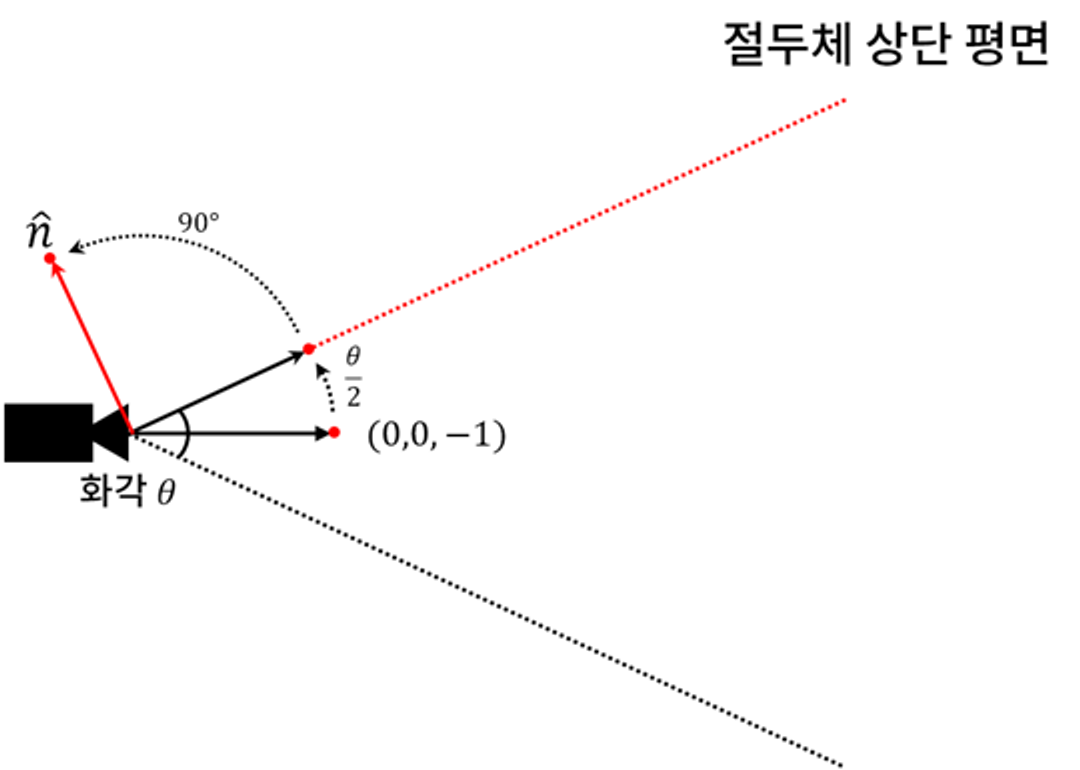
측면에서 바라본 절두체이고 해당 좌표계는 뷰 좌표계이다.
그러므로 해당 평면에서 오른쪽은 -z , 위쪽은 +y에 해당한다.
화각을 θ라고 했을 때,
(0, 0, -1)를 θ/2 만큼 반시계 방향으로 회전시키면
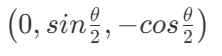
이와 같은 값이 나오게 된닫.
그렇다면 평면의 법선 벡터는 여기서 90'만큼 더 회전한 값이므로
삼각함수에 π/2 만큼 더해주면 될 것이다.
그러면 최종적으로

이와같은 식이 나오고
이것이 평면의 법선 벡터가 된다.
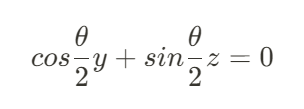
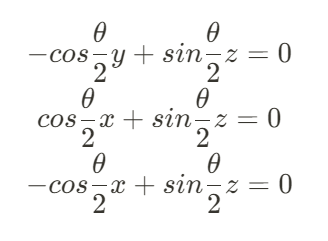
나머지 평면도 대동소이하게 구할 수 있다.
마지막으로 근평면과 원평면의 방정식에 대해 알아보자.
근평면의 경우 원점으로부터 거리는 n이고 법선벡터가 (0, 0, 1) 이므로
(0, 0, 1)ㆍ(x, y, z) - (0, 0, 1)ㆍ(0, 0, -n) = z + n
원평면의 경우 원점으로부터의 거리는 f이고 법선벡터가 (0, 0, -1) 이므로
(0, 0, -1)ㆍ(x, y, z) - (0, 0, -1)ㆍ(0, 0, -f) = - z - f
이제 이 6개의 평면의 방정식을 이용해서 주어진 점이 절두체 외부에 있는지 판단하면 된다.
원근 투영 행렬로부터 평면의 방정식 만들기
원근 투영 행렬을 활용해 절두체 컬링을 좀 더 간편하게 구현할 수 있다.
뷰 공간의 점이 NDC 좌표까지 변환됐을 때 NDC 좌표를 구성하는 x, y, z 세 축의 값이 [-1, 1] 범위에 있다면 해당 점은 절두체 영역 안쪽에 있음을 의미한다.
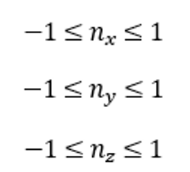
NDC 좌표는 클립 좌표의 마지막 차원 w로 나눈 결괏값이므로, 위 수식을 클립 좌표로 바꿔 쓰면 다음과 같다.
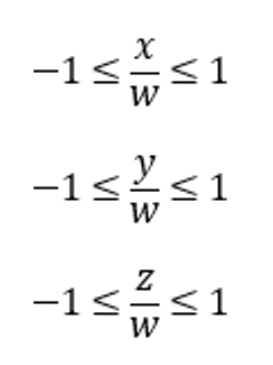
양 변에 w을 곱하면 다음의 부등식을 얻을 수 있다.
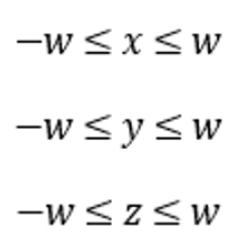
이 상황에서 뷰 공간에서 클립 공간으로 변환하는 과정을 살펴보자.
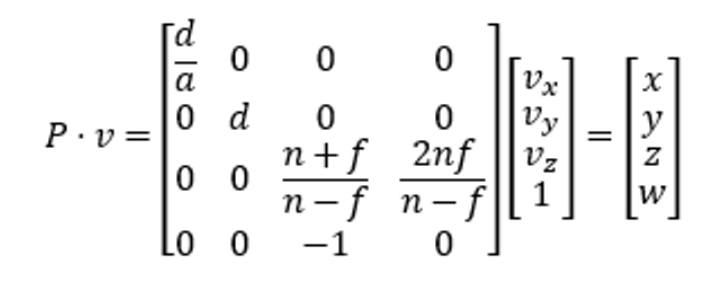
위 식을 행렬의 행벡터와 백터의 내적을 사용해 표기하면 다음과 같다.
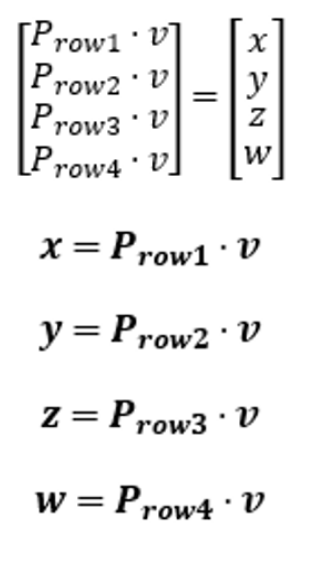
그러면 아까 부등식을 다시 가져와보자.
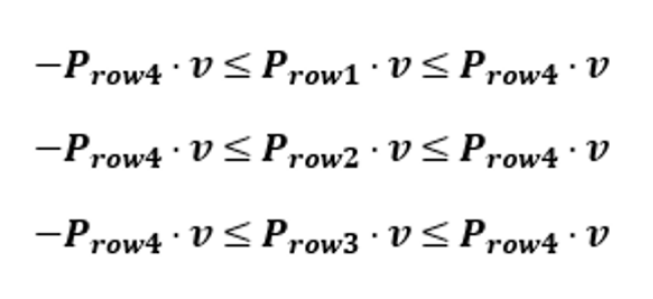
아까 부등식에 원근 투영 행렬의 요소를 대입하면 위와 같다.
위 식을 분리해 총 6개의 부등식으로 나타내보자.
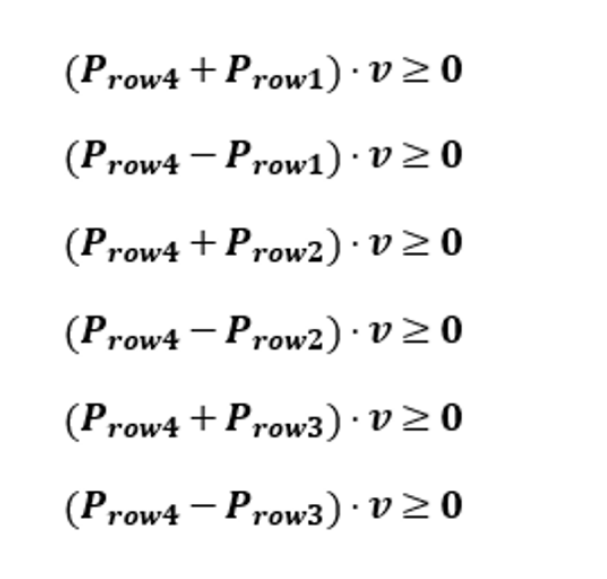
6개의 부등식이 모두 참이면, 뷰 공간의 점 v는 절두체 내부에 있음을 의미하고
하나라도 만족하지 못하면 절두체 영역 외부에 있음을 의미한다.
위 식에서 괄호안의 원근 투영 행렬의 행벡터를 계산한 4차원 벡터를 (a, b, c, d) 라고 하자.
그러면 (a, b, c, d) ㆍ(x,y,z,1) 의 결과는 평면의 방정식과 동일하다.
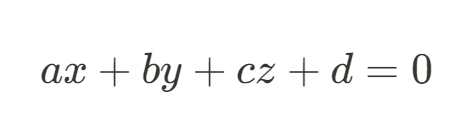
해당 평면의 방정식은 정규화식이 아니므로 정규화하면 다음과 같다.
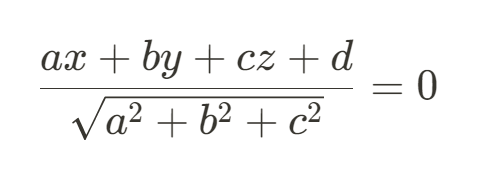
어떤 점 (x, y, z) 에 대해서 위 정규화 평면 방정식에 대입했을 때 값이 0 이상이라면 해당 점은 절두체 내부에 있다는 것을 알 수 있다.
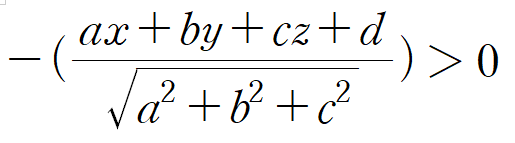
절두체 컬링을 구현할 때는 해당 점이 외부에 있는지 파악하는 수식이 필요하기에, 부호를 반전시켜서 위와같은 부등식을 사용하면, 절두체 밖에 있는 점을 감지할 수 있다.
바운딩 볼륨
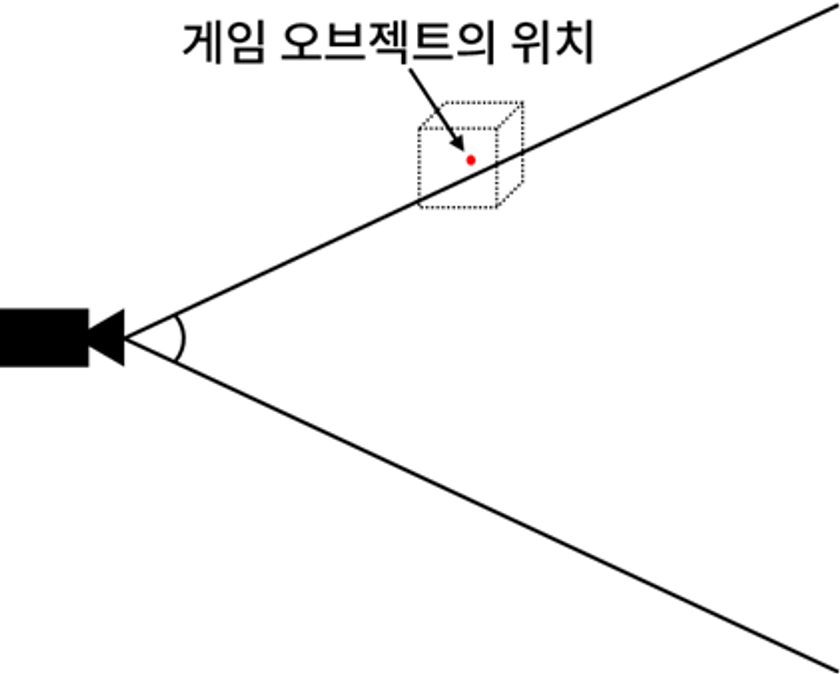
절두체 컬링 알고리즘은 게임 오브젝트의 기준 위치만 가지고 절단을 수행한다.
그러므로 해당 아록리즘에서는 게임 오브젝트의 중심이 바깥에 있고 메시가 공간 영역에 걸쳐서 존재한다면, 그리기를 건너뛸 것이다.
하지만 이 오브젝트는 결국 그려져야 하는 것이 타당하다.
이 문제를 해결하기 위해서는 게임 오브젝트의 위치를 절두체 컬링의 대상으로 하는 것이 아닌, 메시가 차지하는 영역을 감안해 절두체 컬링을 진행해야 한다.
게임 엔진은 메시가 차지하는 영역을 관리하기 위해 구, 박스와 같은 원시 도형을 사용한다.
이러한 원시 도형으로 설정한 공간 데이터를 바운딩 볼륨 이라고 한다.
구 바운딩 볼륨의 판정
구를 통해서 바운딩 볼륨을 판정하는 것은 간단하다.
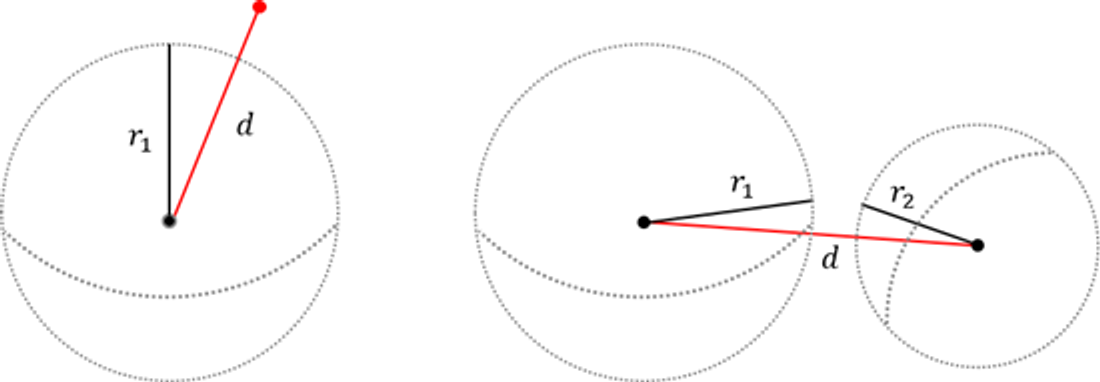
어떤 구O와 어떤 점 P가 존재한다고 하자.
구 O의 중심점과 P의 거리를 d라하고, 구 O의 반지름을 r이라고 하자.
그러면 d > r 이면 점은 구 외부에 있다. d = r 이면 점은 구에 존재하고 d < r 이면 어떤 점은 구 내부에 존재할 것이다.
어떤 두 구 O1 O2 가 있다고 하자.
이 구들이 겹쳐있는지 아닌지 검사하는 것도 간단하다.
두 구의 중심점 거리를 d, 두 구의 반지름을 r1, r2 라고 했을 때
두 구가 떨어져 있는 경우 d > r1 + r2 이고
두 구가 겹질경우 d < r1 + r2 이다.
이제 젤두체 평면과 구와의 내외부 혹은 겹침 판정을 고려해보자.

구의 정점 좌표와 정규화 평면의 방정식 법선 벡터를 (a, b, c) 라고 하자.
이 둘의 내적값에 d를 더한 값이 만약 구의 반지름 r보다 크다면 구는 평면을 완전히 벗어난다는 의미이다.
이런 경우는 그리기를 스킵한다.
만약, 내적값+d 의 절댓값이 r 이하라면, 구는 절두체와 겹쳐있고
나머지 경우, 구는 절두체 내부에 있다고 판단할 수 있다.
구 바운딩 볼륨을 사용하기 위해서는 해당하는 구 영역을 생성해야 하는데, 이는 메시를 구성하는 모든 점의 위치 값을 평균 내 중점 위치를 계산한 후, 중점에서 가장 먼 점과의 거리를 구의 반지름으로 잡으면 무난하다.
바운딩 볼륨 최적화
바운딩 볼륨 정보는 로컬 좌표계를 이용하여 계산된다.
절두체 컬링 자체는 뷰 공간에서 진행되기에, 컬링을 하려면 바운딩 볼륨을 모두 변환시켜야 한다. 이는 조금 부담스러울 수 있다.
대신 절두체를 로컬 공간으로 변환하면 더욱 효율적으로 컬링을 수행할 수 있다.
뷰 공간에서 클립 공간하는 변환은 다음과 같다.
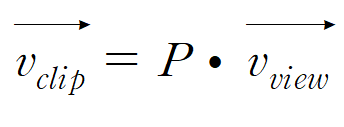
이 때, P는 원근 투영 행렬이다.
뷰 좌표계를 얻어내기 위해서는 로컬 좌표계에 모델링 행렬과 뷰 행렬을 곱해야한다.
그러므로 식을 아래와 같이 바꿀 수 있다.
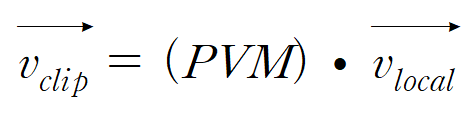
세 행렬을 곱한 PVM 행렬의 행벡터를 사용하여 절두체를 만들어 낼 수 있다.
해당 절두체 정보를 이용하여 로컬 공간에서 절두체 컬링을 하는 것이 가능하다.
AABB와의 판정
이번엔 구 대신 박스 영역을 사용해서 더 정교한 절두체 컬링 작업을 수행해보자.
먼저 박스 바운딩 볼륨을 생성해보자. 박스 영역을 구성하는 각 축의 최댓값 최솟값을 설정하고, 메시를 구성하는 점을 순회하면서 현재 박스의 최댓값과 최솟값을 갱신해나가면 된다.
모든 점에 대해 이 과정을 거치면 기저 축에 평행한 박스 영역이 형성된다.
기저 축에 정렬되어 있다는 의미로 해당 바운딩 볼륨을 AABB (axis aligned bounding box) 라고 부른다.
AABB 영역과 평면과의 판정을 진행해보자.
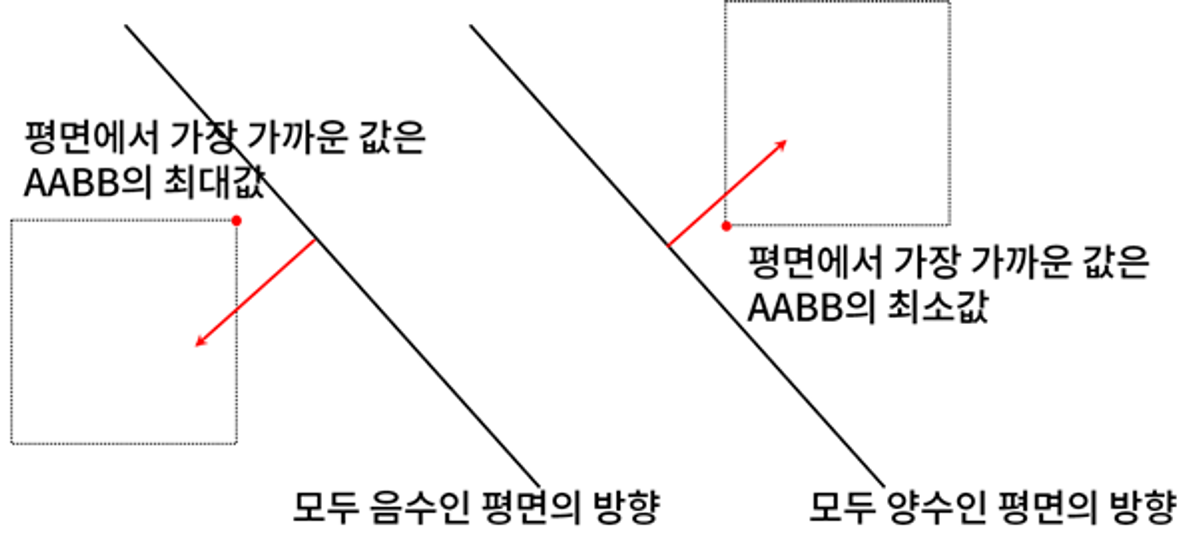
평면의 모든 법선 벡터가 (+, +, +) 경우에, AABB 영역이 평면 밖에 있다고 가정해보자.
그렇다면 AABB 영역의 최솟값 좌표 (min, min, min) 과 평면간의 차이를 구했을 때, 이 값이 양수라면 영역이 평면의 바깥에 위치해 있다고 판단할 수 있다.
반대인 경우도 동일하다. 평면의 모든 법선 벡터가 (-, -, -) 인 경우에는 AABB 영역의 최댓값 좌표 (max, max, max) 과 평면간의 차이를 구했을 때, 이 값이 양수인 경우 AABB 영역이 평면의 바깥에 위치해 있다고 판달할 수 있다.
이는 평면에서 가장 가까운 AABB의 점을 구하는 것이다.
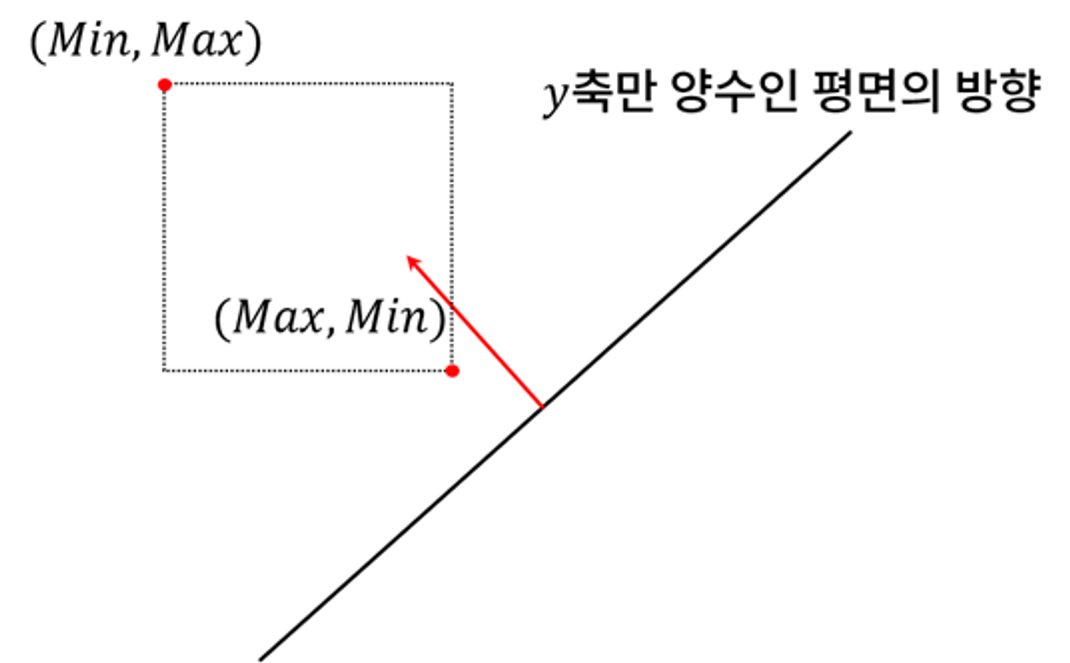
AABB 영역과 법선 벡터의 x, y, z 축은 서로 직교하고 있으므로 각 축의 데이터는 독립적으로 동작한다.
따라서 각 법선 벡터의 양수요소의 경우 AABB의 min값을, 법선 벡터의 음수 요소의 경우 AABB의 max값을 사용하는 것으로 가장 가까운 AABB 영역의 점을 구할 수 있다.
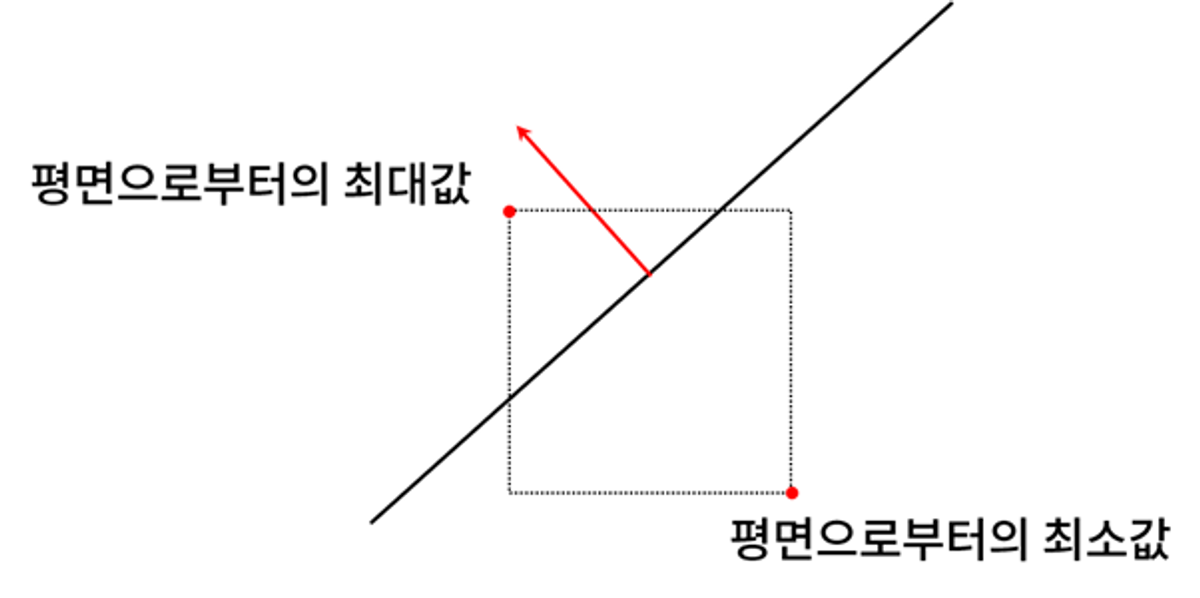
이번에는 AABB 영역이 절두체의 평면과 교차되는 경우를 판단해보자.
평면에서 가장 가까운 AABB의 좌표와 평면과의 차이가 음수가 나올 경우,
판단에 사용한 AABB의 좌표와 정반대에 위치한 점으로 다시 평면과의 테스트를 진행해 평면과의 교차 여부를 확인한다.
정반대에 위치한 점과 절두체 평면과의 차이를 측정한 값이 양수가 나오면 서로 교차한다.
만약 이 값 또한 음수가 나온다면 AABB 영역은 내부에 위치한다.
AABB 바운딩 볼륨은 구 바운딩 볼륨에 비해 계산량은 많지만, 좀 더 정교하게 절두체 컬링을 수행할 수 있다.
삼각형 클리핑
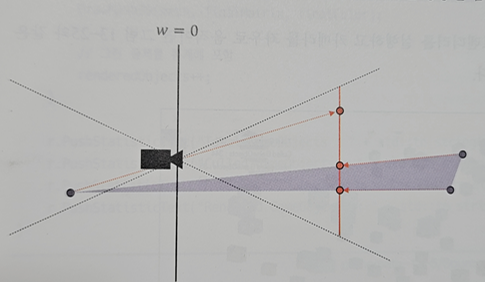
카메라 바로 아래 매우 큰 삼각형이 존재한다고 하자.
위 예시에서는 두 점은 카메라의 앞에, 한 점은 카메라의 뒤에 위치한다.
카메라 뒷편에 있는 부분은 그려지지 않는 게 마땅할 것이다.
그런데 해당 점은 NDC 좌표계로 투영되게 된다.
만약 이를 렌더링한다면 엉뚱한 삼각형이 그려지게 된다.
올바르게 물체를 그려내기 위해서는 카메라 뒤쪽에 있는 점을 파악해서 투영되지 않도록 조치해야한다.
원근 투영 행렬을 곱해 생성된 클립 좌표계의 w값은 뷰 공간에서의 깊이 값을 의미한다. (정확히는 초점 거리)
따라서 카메라 정면에 위치한 점의 w값은 0보다 크고, 카메라 뒤에 있는 점의 w값은 0보다 작다.
따라서, w값보다 작은 영역에 있는 삼각형을 파악해서 잘라내야 한다.
이를 삼각형 클리핑이라고 한다.
삼각형 클리핑 작업은 투영한 후의 좌표를 이용해서 진행한다.
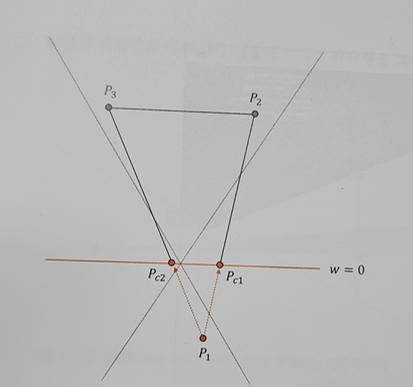
해당 좌표는 절두체를 내려다본 상황이다.
삼각형의 두 w값은 양수이고
나머지 점의 w값은 음수이다.
클리핑을 위해서는 음에 영역에 위치한 부분 삼각형을 잘라내야 한다.
그러기 위해서는 Pc1, Pc2 의 좌표를 알아내야 하는데, 이는 아핀결합의 직선의 방정식을 통해서 쉽게 구할 수 있다.
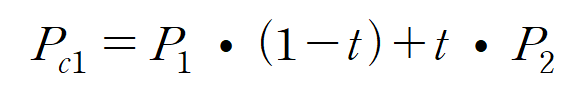
여기서 각 좌표의 w값만 보도록 하자.
Pc1의 w값은 0이다. 그러므로 식을 다음과 같이 정리할 수 있다.
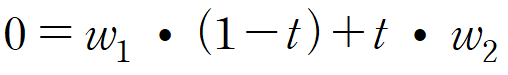
이를 전개해서 t를 얻어내보자.
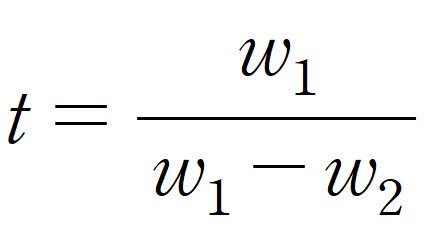
t 의 값을 구한 후
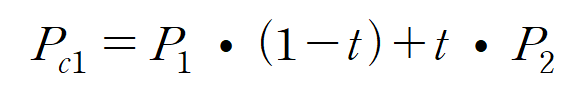
이 식에 대입하면 최종 Pc1 의 좌표를 얻을 수 있고, Pc2도 동일한 방법으로 구할 수 있다.
클리핑한 도형은 다음과 같다.
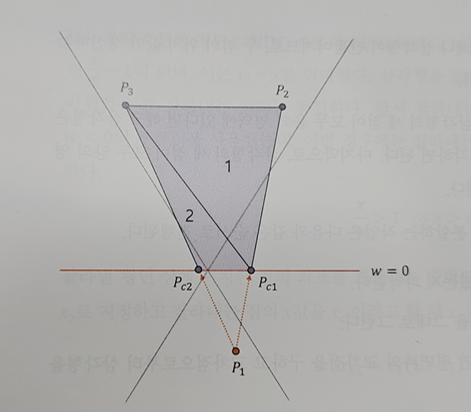
문제점은 해당 도형이 삼각형이 아니라는 것이다.
그러므로 두 개의 삼각형으로 분할해야 하는데, 이 때 주의할 것은 정점의 순서도 자르기 전의 삼각형의 순서와 동일해야 한다는 것이다.
이제, 반대의 삼각형의 경우를 살펴보자.
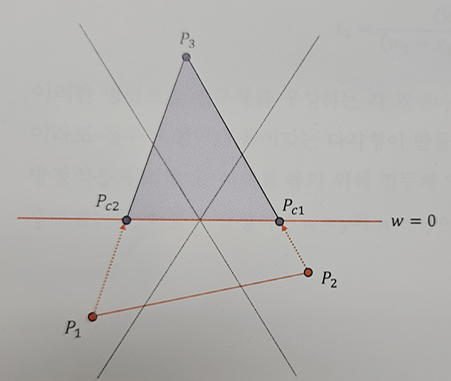
이 또한 아핀 결합 식을 사용해 w = 0 에 위치한 점을 찾을 수 있다.
이 경우 항상 삼각형이 만들어지므로, 두 점의 위치 값만 갱신하면 손쉽게 잘라낼 수 있다.
나머지 경우를 생각하면
모든 점이 음수 영역에 있을 경우인데, 이는 삼각형을 안그리면 되고
모든 점이 양수 영역에 있을 경우에는 삼각형을 그냥 그리면 된다.
아핀 결합을 통해 클리핑을 하는 방법은 사실, 절두체를 구성하는 모든 평면에 사용할 수 있다.
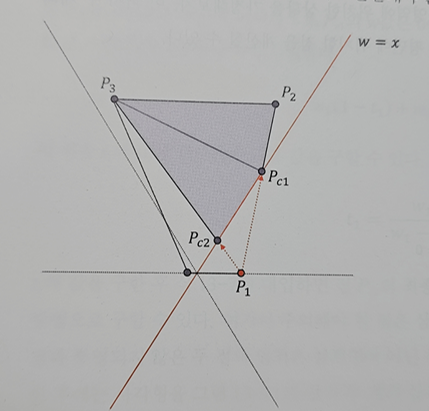
오른쪽 절두체 평면에 대해서 클리핑을 진행한다고 해보자.
절두체의 오른쪽 평면 NDC 좌표의 x값이 언제나 1인 평면인데, 이를 클립 좌표계로 표현하면 x/w = 1이며, x = w를 의미한다.
삼각형을 잘라내는 평면의 식이 w = 0 에서 w = x로 바뀌었을 뿐 잘라내는 원리는 동일하다.
w > x 인 영역이 잘라내야하는 영역이다.
점 Pc1 의 좌표를 구해보자.
Pc1의 x좌표는 다음과 같이 구할 수 있다.
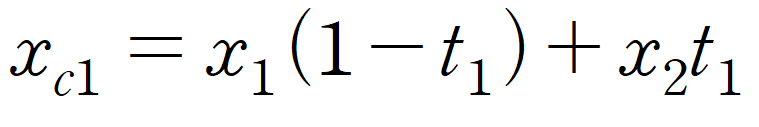
x = w 이므로 다음과 같은 식도 성립한다.
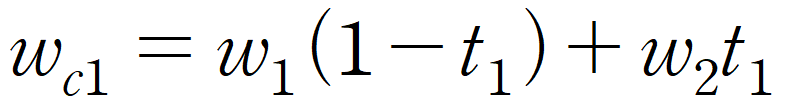
오른쪽 절두체 평면에서는 x와 w값이 동일하므로 아래와 같은 식을 얻어낼 수 있고
이를 사용해 t에대한 식을 도출할 수 있다.
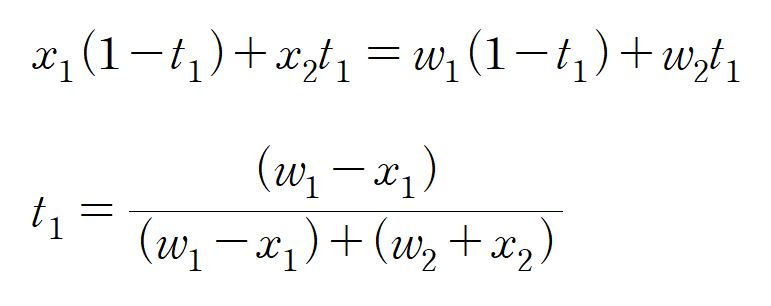
이러한 방법으로 절두체를 구성하는 각 평면마다 삼각형 자르기를 진행하면
클리핑을 수행할 수 있다.
모든 절두체 평면에 대한 판별식은 다음과 같다.
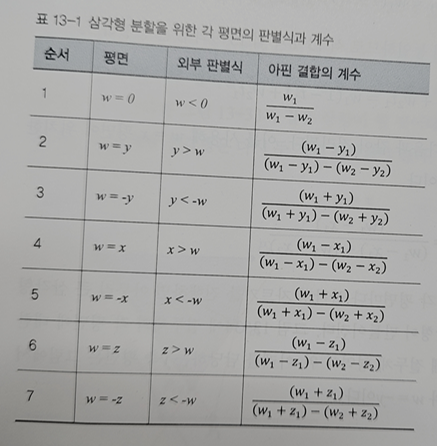
연습문제
1. 평면에 방정식과 관련된 질문이다. 적절하게 대답하라.
(1) 3차원 공간의 한 점 P0와 벡터 n이 주어졌을 때, 이 두 정보를 이용하여 평면의 방정식을 유도할 수 있다. 그 과정을 서술하시오.
(2) 평면의 방정식에서 상수 부분이 의미하는 것은 무엇인지 설명하시오.
설명에는 상수의 기하학적 의미, 상수의 부호에 따른 의미 변화 등이 포함되어야 함.
(3) 어떤 점 point를 받고 정규화되지 않은 방향벡터 directVector를 받았을 때, 방향벡터와 d를 설정하는 식을 적어라
그리고 평면의 방정식을 정규화 하는 부분을 채워라
class Plane
{
public:
Plane() {}
Plane(Vector3D point, Vector3D directVector) { DefinePlane(point, directVector); }
Plane(float a, float b, float c, float d) : normalVector(a, b, c), D(d) {}
void DefinePlane(Vector3D point, Vector3D directVector)
{
//1
}
void Normalize()
{
//2
}
friend std::ostream& operator<<(std::ostream& os, const Plane& plane)
{
static const unsigned int BUFFER_MAX = 256;
char buffer[BUFFER_MAX] = {};
sprintf_s(buffer, BUFFER_MAX, "법선벡터 (%.2f, %.2f, %.2f) d : %.2f\n", plane.normalVector.x, plane.normalVector.y, plane.normalVector.z, plane.D);
os << buffer;
return os;
}
float GetD() const
{
return D;
}
Vector3D GetNormalVector() const
{
return normalVector;
}
private:
Vector3D normalVector = {};
float D = 0.f;
};
(4) 2x + 4y + 9z - 4 = 0 과 같은 평면의 방정식이 있을 때, 주어진 점 P가 평면의 내부에 있는지 외부에 있는지 판단하라.
(-0.65, 4.08, 0.79)
(2.80, -2.64, -3.01)
(-3.87, 3.60, -2.04)
(1.01, -0.33, -2.97)
(-3.93, -3.77, 4.28)
(4.33, -3.43, 2.86)
(-3.11, -2.04, 3.47)
(2.45, 3.13, 2.08)
(3.99, -2.70, 4.14)
(2.57, -4.33, 0.79)
(5) -3x + 2y + z - 4 = 0 과 같은 평면의 방정식이 있을 때, 주어진 점 P와 평면의 최단거리를 구하라
(-0.65, 4.08, 0.79)
(2.80, -2.64, -3.01)
(-3.87, 3.60, -2.04)
(1.01, -0.33, -2.97)
(-3.93, -3.77, 4.28)
(4.33, -3.43, 2.86)
(-3.11, -2.04, 3.47)
(2.45, 3.13, 2.08)
(3.99, -2.70, 4.14)
(2.57, -4.33, 0.79)
2. 근평면과 원평면을 제외한 평면들의 평면 방정식의 d값이 0인 이유가 무엇인가?
3. 절두체를 이루는 평면들의 평면 방정식을 모두 유도하시오.
(1) 한 점과 노말벡터를 이용하여 게산하는 방법
(2) 원근 투영 행렬을 이용하여 계산하는 방법
4. 절두체와 평면과 점 내외부 판단 방정식만으로 절두체 컬링 알고리즘을 구했을 때 한계점을 서술하고, 해결방법을 서술
하시오. 해당 해결방법으로 절두체 컬링 알고리즘을 구현하는 방법과 해결하는 이유를 자세하게 설명하시오.
5. 바운딩 볼륨이 필요한 이유를 절두체 컬링 알고리즘의 한계점과 엮어서 설명하시오. 그리고 바운드 볼륨으로 어떻게 해당 한계점을 해결하는지 설명하시오.
6. 다음과 같은 구와 점이 주어져있을때 내외부 혹은 겹침을 판단하라.
내부 혹은 겹침 상태면 Yes를 아니면 No
구1
중심 : (1.2,-2.5, 3.3)
반지름 : 6
점 판정
(-3.22, 3.21, -0.62)
(-0.28, 3.52, -2.07)
(-2.06, -2.99, 2.02)
(-1.48, -0.66, 1.36)
(-2.07, 3.82, 2.83)
(3.63, 0.68, -3.29)
(0.62, -0.61, -4.73)
(0.01, 1.91, 3.42)
(-0.90, 1.19, -4.19)
(1.43, 1.40, -3.92)
구 판정
중심 (-4.05, 2.82, 6.26) 반지름 : 4.23
중심 (-1.16, 1.04, 5.44) 반지름 : 2.54
중심 (9.60, 6.98, 2.21) 반지름 : 3.79
중심 (8.06, -1.37, 3.28) 반지름 : 2.65
중심 (-7.81, 3.84, 8.40) 반지름 : 3.09
중심 (-2.99, -5.64, -2.73) 반지름 : 0.70
중심 (7.93, -1.57, 9.31) 반지름 : 2.06
중심 (6.38, 2.64, 2.33) 반지름 : 2.89
중심 (6.66, 9.06, -5.74) 반지름 : 1.72
중심 (3.79, -6.44, 1.71) 반지름 : 4.54
7. 평면의 방정식과 구에 대한 정보가 주어졌을 때, 해당 구가 평면의 외부에 있는지, 겹쳐있는지, 내부에 있는지 탐지해보자.
콘솔창에 내부, 외부, 겹침
등으로 출력하시오.
평면의 방정식 : 2x + 9y + 5z + 2 = 0
원
중심 (1.00, 7.29, -0.84) 반지름 : 0.76
중심 (-7.60, -1.56, -6.71) 반지름 : 3.62
중심 (2.91, -6.59, -9.48) 반지름 : 1.79
중심 (5.09, -0.07, -3.25) 반지름 : 1.96
중심 (2.53, 9.48, -3.90) 반지름 : 1.64
중심 (-5.96, -8.78, 2.19) 반지름 : 1.19
중심 (0.10, -5.86, -2.63) 반지름 : 0.30
중심 (-3.85, -0.13, 1.37) 반지름 : 1.26
중심 (3.73, 4.82, 2.73) 반지름 : 0.09
중심 (8.36, -1.09, 2.06) 반지름 : 4.26
8. 모든 바운딩 볼륨을 뷰 공간으로 변환하여 절두체 컬링을 하는 것은 비효율적이다. 그렇다면 효율적으로 절두체 컬링을 진행하는 방법에 대해서 설명하시오.
9. 어떤 메시에서 구 영역 바운딩 볼륨과 AABB 영역 바운딩 볼륨을 생성하는 방법을 하나씩 제시하라.
10. 평면과 박스 영역이 주어질 때, 박스가 평면의 외부에 있는지 내부에 있는지 겹쳐있는지 판별하라.
<케이스 1>
법선벡터 (1.00, -7.00, 3.00) d : -8.00
최대점 (0.00, 5.08, 2.83) 최소점(-7.65, -7.28, -8.57)
<케이스 2>
법선벡터 (-2.00, 1.00, -3.00) d : 4.00
최대점 (2.14, 8.01, 0.00) 최소점(-4.62, 1.11, -9.98)
<케이스 3>
법선벡터 (1.00, -2.00, 7.00) d : -3.00
최대점 (8.15, 0.00, 0.09) 최소점(-0.40, -7.15, -9.79)
<케이스 4>
법선벡터 (8.00, -3.00, 5.00) d : 7.00
최대점 (0.00, 3.23, 1.22) 최소점(-9.11, -5.27, -6.70)
<케이스 5>
법선벡터 (7.00, 9.00, -4.00) d : -9.00
최대점 (7.37, 3.37, 5.44) 최소점(-7.49, 1.41, -1.47)
<케이스 6>
법선벡터 (8.00, -8.00, -4.00) d : 1.00
최대점 (8.01, 6.87, 0.00) 최소점(5.01, 3.64, -8.82)
<케이스 7>
법선벡터 (1.00, -4.00, 8.00) d : -6.00
최대점 (2.22, 7.09, 0.00) 최소점(1.00, -9.97, -7.31)
<케이스 8>
법선벡터 (-8.00, -1.00, 1.00) d : -9.00
최대점 (8.45, 5.21, 8.56) 최소점(-5.82, -7.13, -3.37)
<케이스 9>
법선벡터 (-7.00, -1.00, 1.00) d : 1.00
최대점 (3.32, 8.79, 4.14) 최소점(-3.56, -1.60, -0.38)
<케이스 10>
법선벡터 (9.00, 7.00, 7.00) d : -6.00
최대점 (6.99, 1.33, 7.97) 최소점(-7.02, -0.54, -1.24)
11. 삼각형 클리핑이 필요한 이유를 간단히 설명하고 4가지 경우에 대해서 삼각형 클리핑이 이뤄지는 흐름을 설명하라.
1) 세 점의 w 값이 모두 양수
2) 두 점의 w 값만 양수
3) 한 점의 w 값만 양수
4) 모든 점의 w 값이 음수
12. 삼각형 클리핑을 수행할 때, 절두체 평면을 기준으로도 삼각형 클리핑을 수행할 수 있다. 원평면을 기준으로 삼각형 클리핑을 수행하고 싶을때 사용할 수 있는 아핀 결합의 계수 방정식을 구하여라
'컴퓨터 그래픽스 > 수학' 카테고리의 다른 글
| [수학] 오일러 공식: 허수로 표현하는 회전 변환 (0) | 2024.07.25 |
|---|---|
| [수학] 복소수: 2차원 평면의 수 (6) | 2024.07.24 |
| [수학] 원근 투영: 화면에 현실감을 부여하는 변환 (11) | 2024.07.20 |
| [수학] 외적: 3차원 공간의 분석과 응용 (3) | 2024.07.20 |
| [수학] 3차원 공간: 입체 공간의 생성 (3) | 2024.07.19 |





