1. 벡터의 외적
3차원 벡터 간의 외적은 X 기호를 사용한다.
3차원 유클리드 공간의 벡터 x=(x1,x2,x3), y=(y1,y2,y3) 의 벡터곱 x X y 는 다음과 같이 정의된다.


외적의 결과는 언제나 3차원 벡터가 된다.
1) 외적의 성질
- 외적은 교환법칙이 성립하지 않는다. (내적과 차이점)
- 외적의 순서를 바꿔 연산하면 반대 방향의 벡터가 나온다.
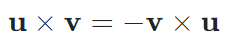
- 외적은 결합법칙도 성립하지 않는다.
- 외적은 덧셈에 대한 분배법칙이 성립한다.
- 결과값은 항상 벡터 값이다.
2) 행렬곱, 내적, 외적 비교
| 행렬곱 | 내적 | 외적 | |
| 계산 결과 | 행렬 | 스칼라 | 벡터 |
| 교환법칙 | X | O | X |
| 결합법칙 | O | X | X |
| 덧셈에 대한 분배법칙 | O | O | O |
2) 외적의 활용 : 평행성 판별
동일한 벡터를 외적하면 항상 영벡터가 나온다.
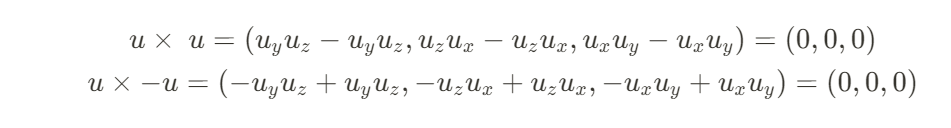
반대방향 벡터를 외적하는 경우에도 동일하다.
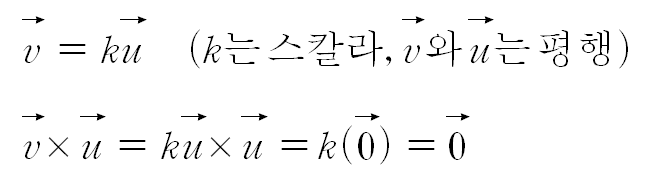
평행하지만 크기가 다른 벡터를 서로 외적해도 0벡터가 나온다.
이로써 평행한 두 벡터를 외적하면 항상 영벡터가 됨을 알 수 있다.
이러한 외적의 성질은 평행성을 판별하는 데 사용된다.
3) 외적 sin 공식 유도

어떤 두 벡터 v, u를 생각해보자.
벡터 u는 벡터 v에 평행한 벡터 u1와 u2 = u-u1 로 나타낼 수 있다.
즉, u = u1 + u2 (단, u1 은 벡터 v와 평행, u2 는 벡터 v와 수직)
v x u = v x (u1 + u2) 이고, 분배법칙에 의해
v x u1 + v x u2 으로 나타낼 수 있다.
u1는 벡터 v와 평행하기에 외적 결과는 영벡터가 된다.
외적은 결국 상대방에 직교하는 벡터 성분만 사용되는 성질이 있음을 알 수 있다.

두 벡터의 사잇각을 θ 라고할 때,
사잇각이 클수록 직교 성분이 커지는 것을 볼 수 있다.그러므로 외적의 크기도 sin 함수에 비례할 것이다.
이를 증명하려면 세 가지 연산 |u x v|² , (|u||v|)² , (uㆍv)² 을 각각 전개하여 관계를 찾으면 된다.|u x v| ² + (u ㆍ v) ² = (|u||v|) ²
이 성립하게 되고, 최종적으로
|u x v| = |u||v| |sin θ|
라는 벡터 외적의 크기 공식이 나온다.
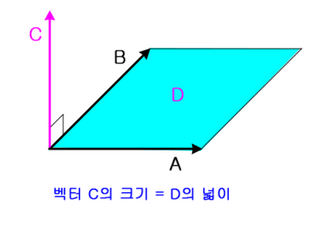
외적으로 생성된 벡터의 크기는 위와같이 두 벡터가 만드는 평행사변형의 넓이로 나타낼 수 있다.
4) 외적의 활용 : 법선 벡터
벡터 외적의 성질 중 하나는 두 벡터에 직교하는 벡터를 생성한다는 것이다.
임의의 두 벡터 u와 v의 외적 결과를 w라고 할 때
uㆍw = vㆍw = 0 이다.
그렇다면 외적의 결과는 두 벡터에 모두 직교함을 알 수 있다.
선형 독립의 관계를 가지는 두 벡터의 선형 결합은 평면을 만들다고 했다.
그렇다면 두 벡터의 외적은 두 벡터가 만드는 평면에 직교하는
다른 표현으로는 평면이 향하는 방향에 대한 벡터를 만들어내는 것으로 해석할 수 있다.
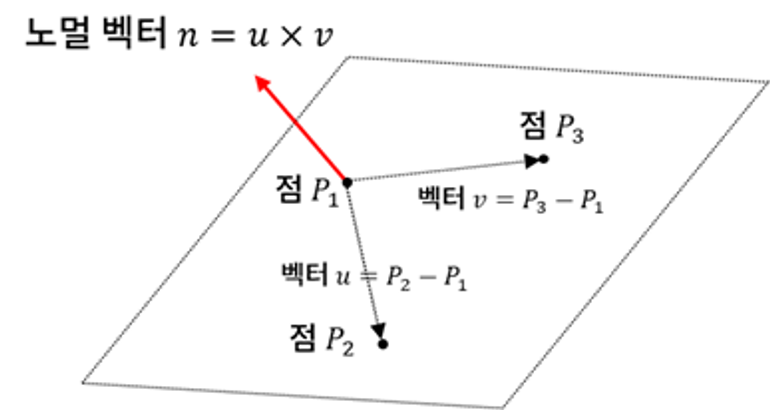
세 점이 존재할 때, 2개의 벡터를 생성해서 외적하면, 세점이 만들어내는 평면에 대한 직교벡터를 얻어낼 수 있다.
이러한 벡터를 '법선 벡터' 또는 '노말 벡터' 라고 부른다.
외적은 교환법칙이 성립하지 않기 때문에,
u x v 와 v x u 는 서로 반대 방향을 표현한다.
따라서 법선 벡터를 생성할 떄에는 외적의 연산 순서에 신경 써야 한다.
5) 외적의 활용 : 좌우 방향 판별
외적의 활용 방법 중 또 다른 하나는 왼쪽과 오른쪽의 판별이다.
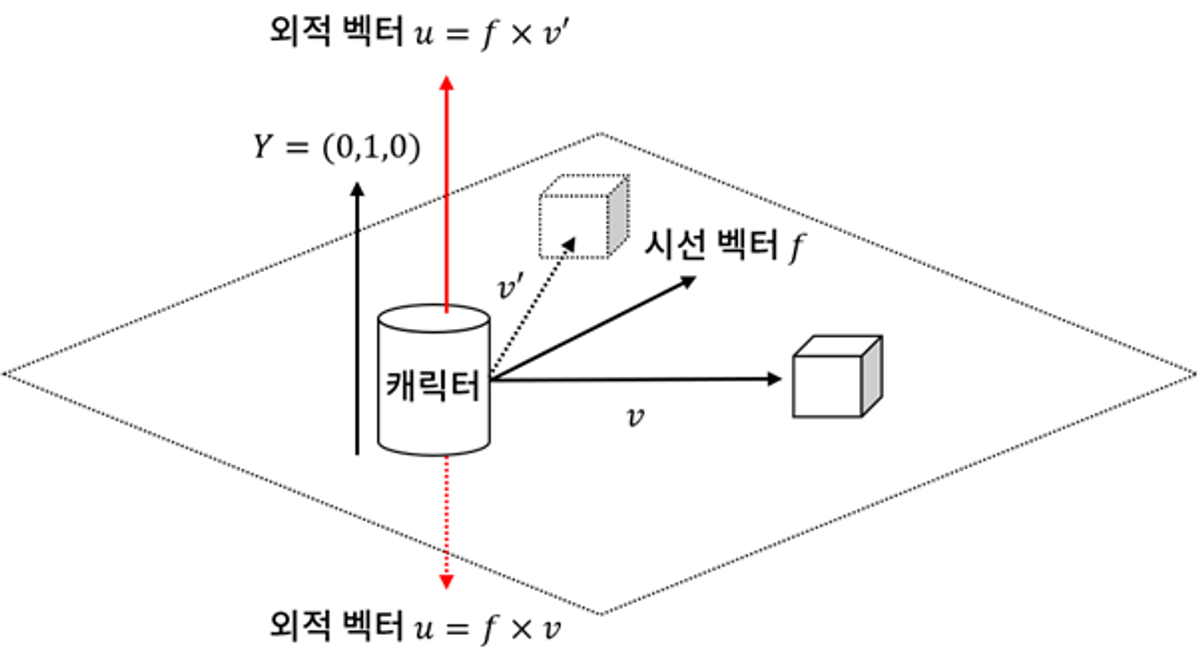
캐릭터와 물체가 있다고 할 떄,
캐릭터의 시선 벡터를 f
캐릭터에서 물체로 향하는 벡터를 v 라고 하자.
만일 물체가 시선 방향의 왼쪽에 있다면
f x v' 는 평면의 윗쪽으로 향할 것이다.
반대로 물체가 시선 방향의 오른쪽에 있다면
f x v 는 평면의 아랫쪽으로 향할 것이다.
이러한 외적의 성질을 활용하면 시선 방향을 기준으로 물체가 왼쪽에 있는지 오른쪽에 있는지를 파악할 수 있다.
외적의 결과는 벡터이므로, 참 거짓을 파악할 수 있도록 평면의 법선 벡터 y와 내적해보자.
두 벡터의 방향이 같다면 내적 값은 양수
반대 방향이랄면 음수가 되고, 방향이 같다면 0이 될 것이다.
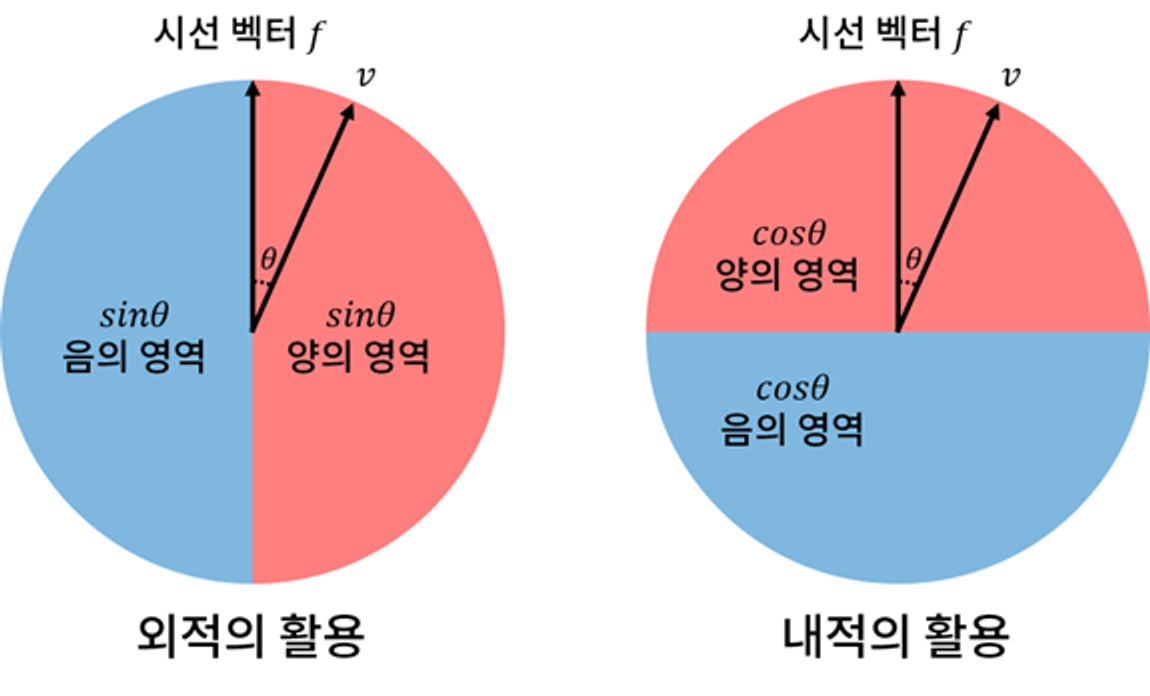
이러한 좌우 방향 판별에 사용되는 외적의 응용은 sin 함수에 비례하는 외적의 성질에 기인한다고 할 수 있다.
2. 벡터로부터 회전행렬 생성
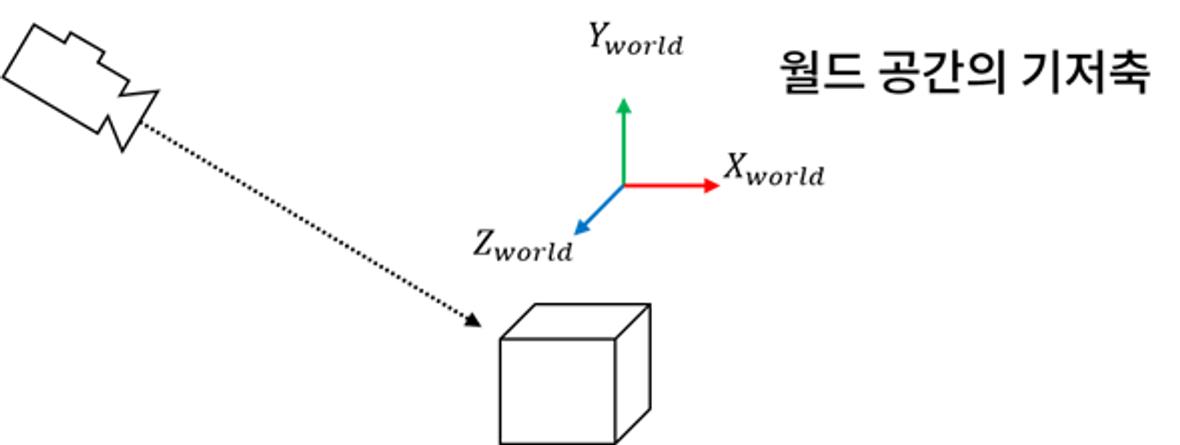
외적의 성질은 카메라의 회전을 설정하는데도 사용된다.
3차원 공간에서 좌우로 기울어지지 않은 카메라가 물체를 바라보고 있다고 설정하자.
오일러 각 방식을 사용해 카메라의 회전을 지정할 수 있지만, 외적을 사용하면 카메라의 시선 벡터 정보로부터 카메라의 세 가지 로컬 축을 구하고 이로부터 회전행렬까지 얻어낼 수 있다.
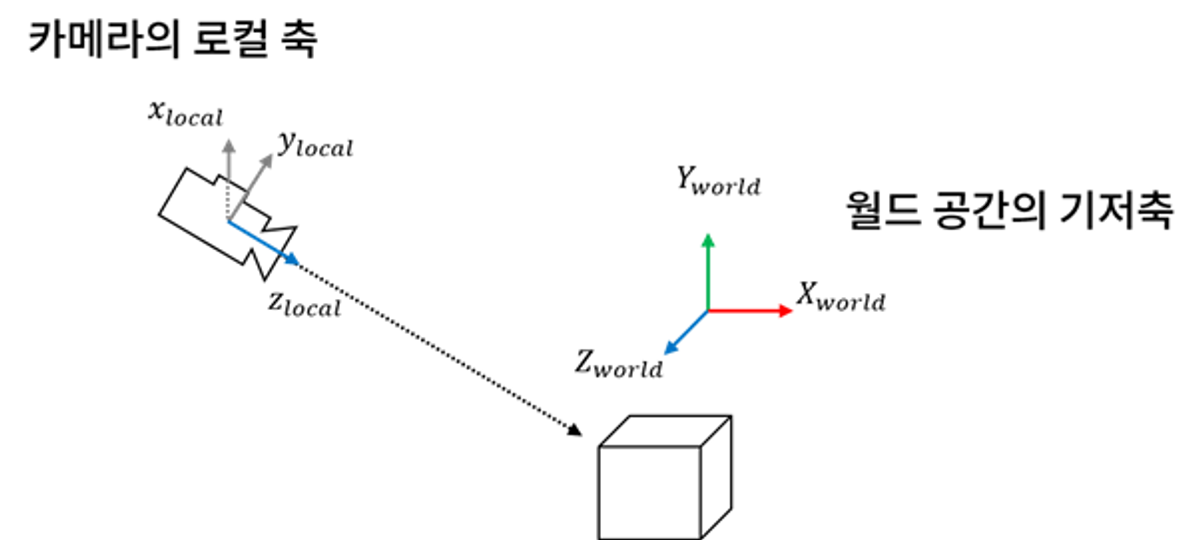
먼저, 믈체의 위치에서 카메라 위치를 뺀 후 크기를 1로 정규화시킨 시선 벡터 v를 생성한다.
이 벡터는 카메라 트랜스폼의 로컬 z축이 된다.
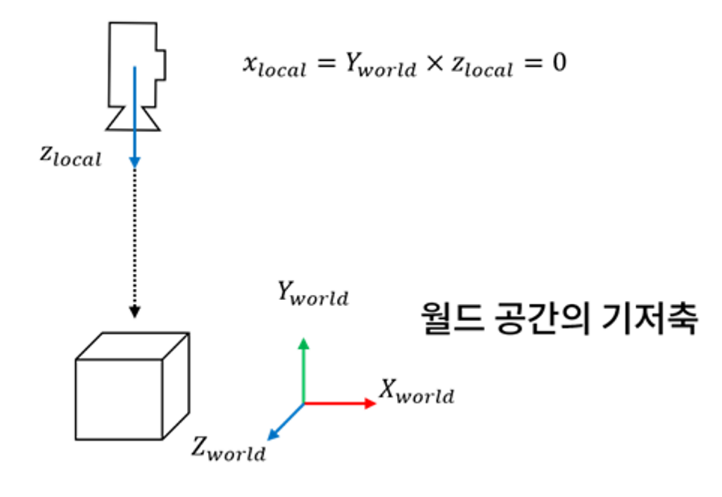
카메라의 로컬 x축은 월드 공간의 y축과 로컬 공간의 z축을 외적하면 얻을 수 있다.
마지막으로 로컬 z축과 x축을 외적하면, 로컬 y축을 구할 수 있따.
이떄, 두 벡터가 단위 벡터이므로 외적의 결과도 단위 벡터가 될 것이다.
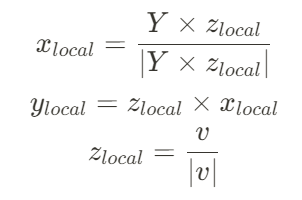
수식으로 정리하면 위와 같다.
Y는 월드 업벡터이다.
그렇다면 카메라 트랜스폼의 회전행렬 R은 로컬 벡터를 열벡터로 지정해 다음과 같이 생성할 수 있다.
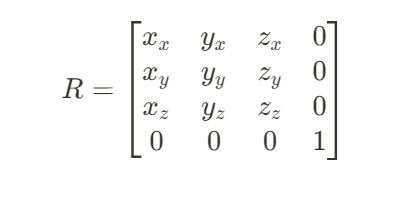
시선 벡터로부터 카메라의 로컬 축을 계산하는 데 있어 추가로 고려해야 할 사항은 '카메라의 위쪽 방향'이다.
앞서 살펴본 방법은 카메라의 위쪽 방향이 월드 공간의 y축을 향한다고 가정한 것이다.
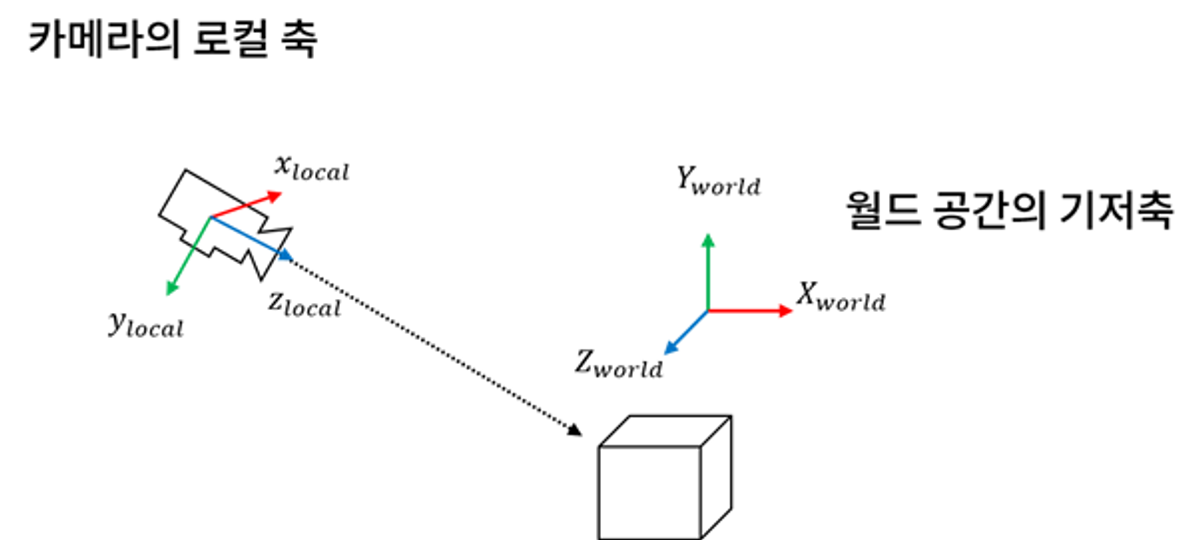
만약 이런식으로 카메라가 뒤집혀 있는 상황도 있기 때문에, 이럴 때는 로컬 x축을 구하기 위한 업벡터로 월드 공간 y축의 반대 방향인 (0, -1, 0) 을 사용해야 한다.
렌더러에서는 외적에 사용된 업벡터의 값을 직접 입력받도록 설계하는 것이 안전하다.
그 다음 고려할 예외 상황이다.
바로 위와같이 로컬 z축이 업벡터와 평행한 때다.
이러면, 로컬 x축을 얻어낼 수 없어 계산을 진행할 수 없다.
이 경우에는 외적을 계산하는 대신, 로컬 z축에 직교하는 로컬 x축의 값을 수동으로 지정해야 한다.
3. 렌더링 계산량을 줄여주는 백페이스 컬링
게임은 실시간으로 빠르게 렌더링을 처리해야 하기에 시선에 감지되는 않는 메시의 뒷면(backface)은 그리지 않고 건너뛰는 것이 효과적이다. 이렇게 카메라와 마주보지 않는 뒷면을 생략하는 기법을 백페이스 컬링이라고 한다.
백페이스 컬링은 메시의 삼각형을 구성하는 세 정점의 외적을 활용해 구현할 수 있다.
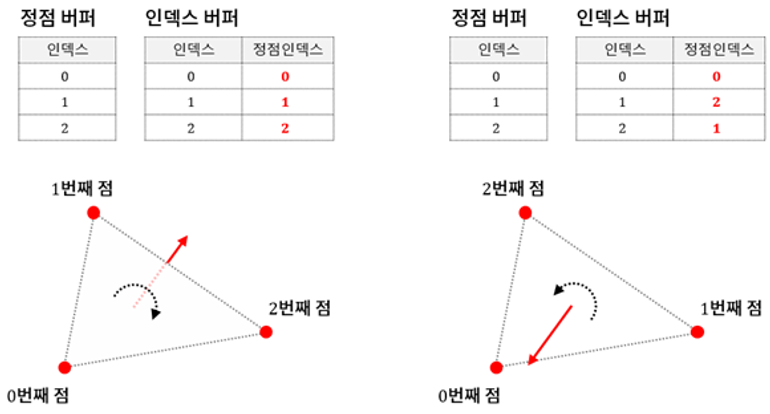
점 세 개로 생성한 삼각형의 방향은 2개의 경우가 존재한다.
삼각형의 세 점을 지정하는 인덱스 버퍼에는 점의 순서가 나열되어 있는데, 이를 활용한다면 삼각형의 방향을 지정하지 않아도 외적을 사용해 삼각형이 향하는 방향을 파악할 수 있다.
왼쪽은 시계 방향으로 정의되어 있기에 뒷면을 향할 것이고
오른쪽은 반시계 방향으로 정의되어 있기에 전면을 향할 것이다.
이렇게 정한 삼각형의 방향과 카메라의 시선 방향과 대조해 서로 마주보면 삼각형을 그리고, 서로 같은 방향을 바라보면 그리기를 생략하는 것이 백페이스 컬링의 알고리즘이다.
서로 같은 방향인지를 판별하는 것은 내적을 이용하면 될 것이다.
4. 오일러 각의 문제를 해결하는 로드리게스 회전 공식
오일러 각은 짐벌락 현상이 발생하고, 회전 보간에 제약이 있다는 문제가 존재한다.
그런데 오일러 각의 문제는 임의의 축에 대한 평면의 회전 방식을 사용하면 해결이 가능하다.
이 방식을 축-각 회전이라 부른다.
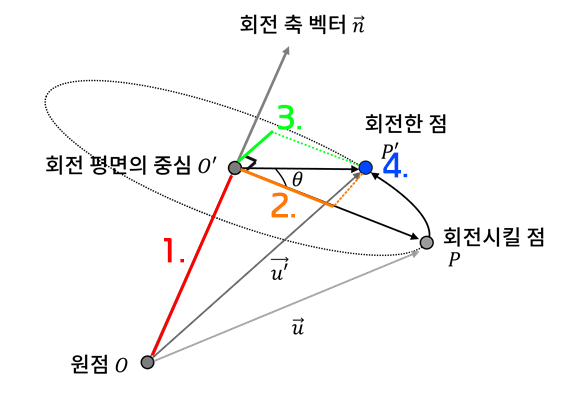
해당 방식은 3차원 공간에서 지정된 임의의 축에 직교하는 평면에서 회전이 진행되는 형태를 띤다.
축-각 회전을 수행하는 회전 공식을 내적과 외적을 사용해 직접 유도해보자.
회전축은 회전이 발생하는 평면에 직교하는 법선 벡터다.
이를 '회전축 벡터 n' 이라고 지정한다.
편의상 n을 정규화한다.
그리고 회전시킬 점을 P
점 P가 각 θ 만큼 회전한 최종 점을 P' 라고 표기하고 ,월드 공간의 원점을 O로, 회전 평면의 중심점을 O'로 지정하자.
이 때 점 P의 좌표는 다음과 같다.
P = (x, y, z, 1)
원점 O에서 회전시킬 점 P까지의 벡터를 u로 지정하자.
점 p와 벡터 u의 값은 마지막 차원의 값만 다를 뿐 (x, y, z)의 값은 동일하다.
따라서 우리가 구할 점 P'의 좌표는 벡터 u를 구한다면 얻을 수 있을 것이다.
u = P - O = (x, y, z, 0)
임의의 축 n에 대해 벡터 u를 각 θ 만큼 회전시켜 벡터 u' 을 계산하는 축각 회전의 공식은 다음과 같다.
u' =
cos θ ㆍu + (1 - cos θ) ㆍ(u ㆍn) ㆍn + sin θㆍ(n x u)
이 공식을 유도해보자.먼저 원점에서 회전시킬 점으로 향하는 벡터 u를 평면의 회전축에 해당하는 법선 벡터 n에 투영해보자.벡터 u가 투영할 벡터 n의 크기가 1이므로, 투영 공식에 의해 벡터 OO'의 값은 (uㆍn) ㆍn 이 된다.줄여서 벡터 v라고 하자.

그렇다면 회전 평면의 중점 O'에서 점 p로 향하는 벡터 O'P 는 두 벡터의 차가 되므로 u - v 가 될 것이다.우리는 O'P 벡터를 각 θ만큼 회전시켜 벡터 O'P' 를 구하는 것이 목표이다.
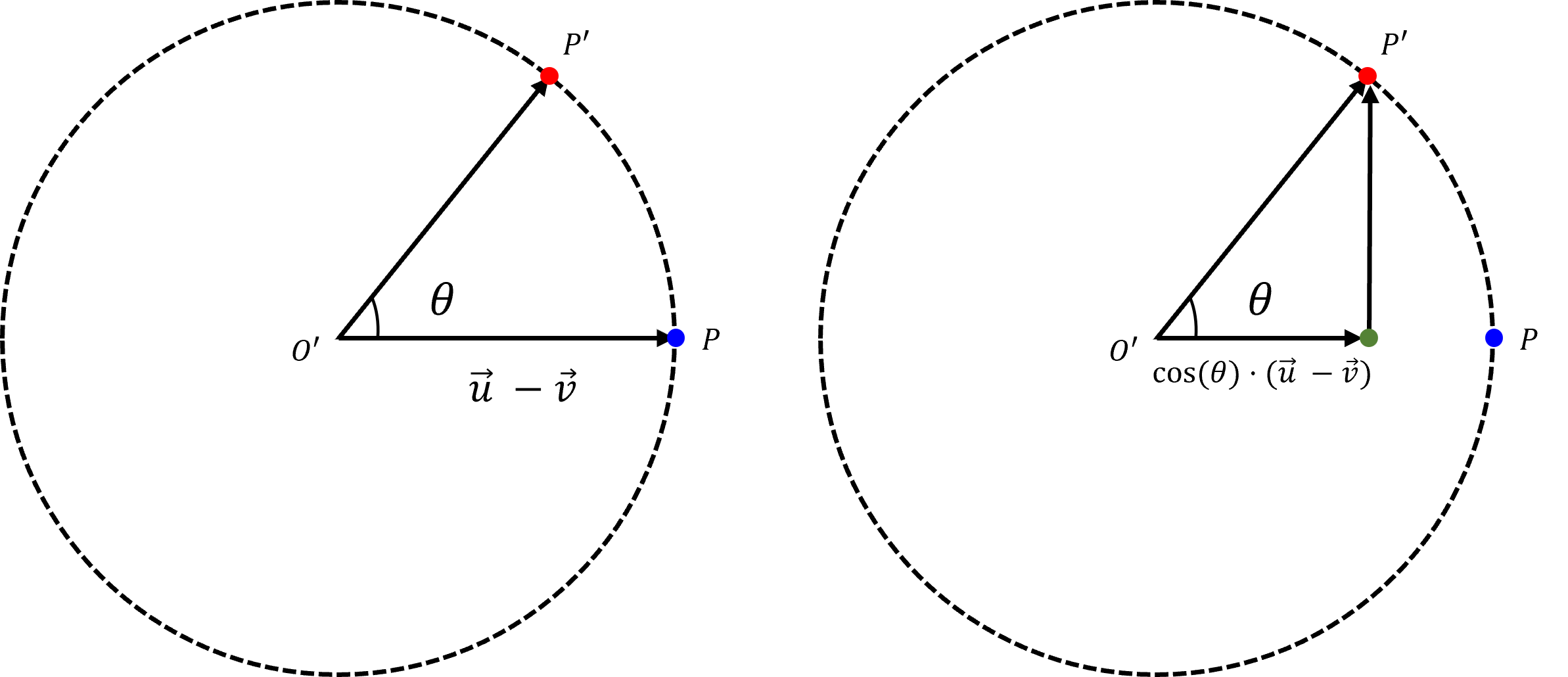
벡터 O'P'를 가로 성분과 세로 성분으로 분리하자
가로 성분에 해당하는 벡터는 삼각함수를 이용해 얻을 수 있으며 이는
cos θㆍ(u - v) 이다.
이제 나머지 세로 성분을 구해야 한다.
세로 성분에 해당하는 벡터를 구하려면 같은 방향을 향하는 벡터가 필요한데
회전축 벡터와 O'P 벡터를 외적해서 구할 수 있다.
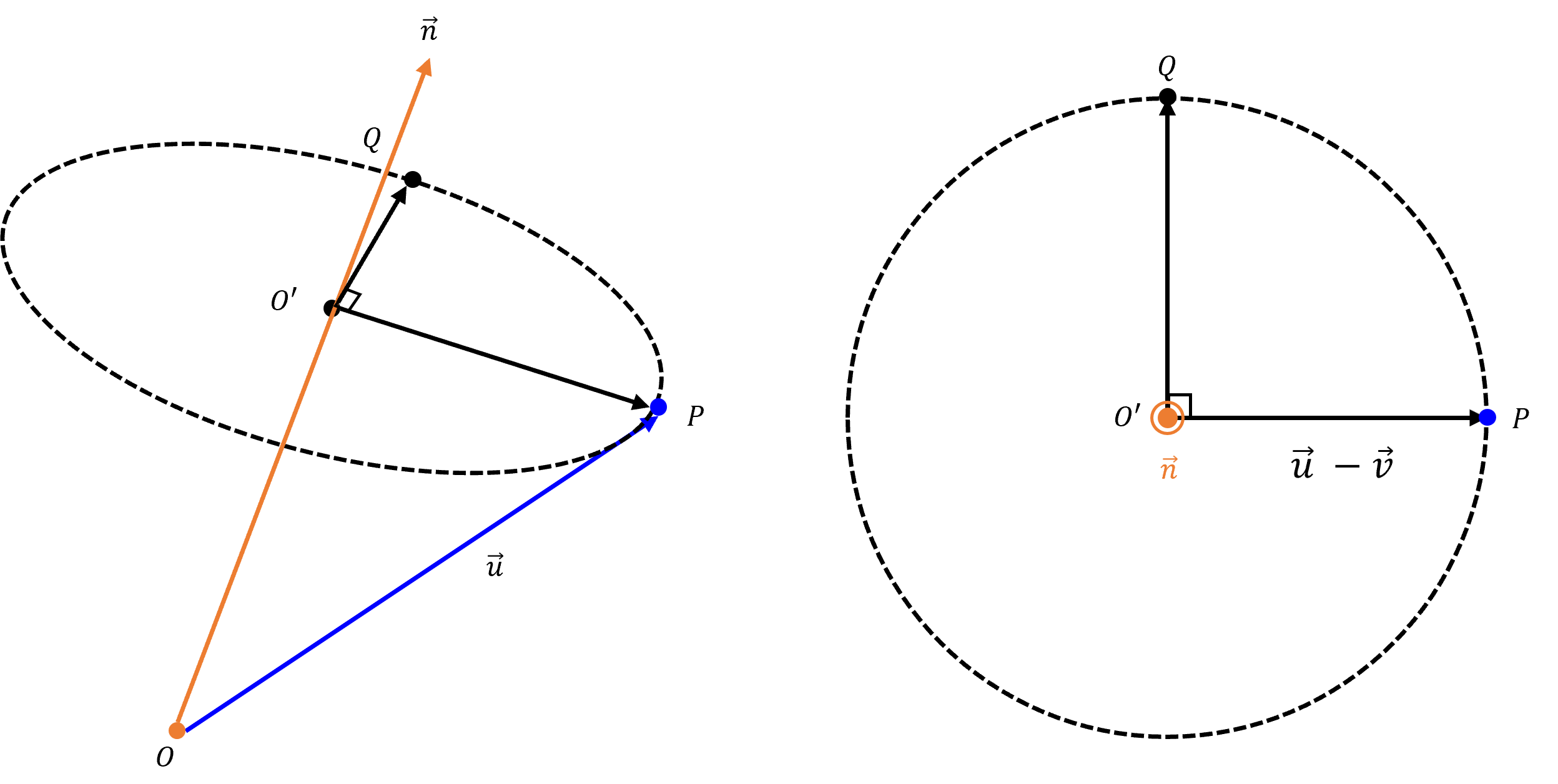
그렇게 얻은 수직벡터와 원이 교차하는 점을 Q라고 하자.
그러면 cos(90 - θ) O'Q 을 하여 수직성분을 구할 수 있을 것이다.
이를 정리하면 O'P' 성분은 다음과 같다.
O'P' = cos θ O'P + sin θ O'Q
위 식을 벡터 n, u와 v를 사용해 전개하면 다음과 같다.
O'P' = cos θ (u - v) + sin θ(n x (u - v))
분배법칙을 적용해 이를 풀어 전개하면 다음과 같다.
O'P' = cos θ (u - v) + sin θ (n x u - n x v)
벡터 n과 v는 평햄하므로 우변의 끝에 위치한 외적 n x v 값은 항상 영벡터가 된다.
O'P' = cos θ (u - v) + sin θ (n x u)
마지막으로 우리가 구할 최종 벡터 OP'는 선분 O'P' 에 벡터 v를 더해 얻을 수 있다.
OP' = v + cos θ (u - v) + sin θ (n x u)
이제 벡터 v를 (u n) n 으로 치환하면 최종 수식이 완성된다.
u' = cos θ ㆍu + (1 - cos θ) ㆍ(u ㆍn) ㆍn + sin θㆍ(n x u)
로드리게스 회전 공식을 활용하면 오일러 각으로 구현하기 어려운 임의의 축에 대한 회전 변환을 수행할 수 있다.
그러나 이 방식은 행렬로의 변환이 어렵고 계산이 복잡하기 때문에 게임 엔진에서는 사원수를 주로 사용한다.
5. 삼중곱
삼중곱이란 벡터의 외적 혹은 내적을 두 번 연속 사용하는 연산을 의미한다.
세 벡터 v, u, w 가 있을 떄 삼중곱이라고 부를만한 상황은 2가지다.
1) v x (u x w)
2) vㆍ(u x w)
1. 스칼라 삼중곱
vㆍ(u x w)
스칼라 삼중곱 연산의 의미를 파악해보자.
vㆍ(u x w) = |v| |u x w| cos θ
라고 할 수 있을 것이다.
u x w는 두 벡터가 만들어 내는 평면의 법선벡터이고
|u x w|는 두 벡터가 만들어 내는 평행사변형의 넓이이다.
또, |v| cos θ는 벡터 u x w 에 내리는 투영 벡터의 크기라고도 볼 수 있다.
그러면 결국
스칼라 삼중곱은 세 벡터가 만들어내는 평행육면체의 부피라고 생각할 수 있다.

이 그림을 통해 알 수 있는 것은
어떤 벡터를 외적하고, 내적하냐 순서에 상관없이 결과는 항상 세 벡터가 만들어내는 평행육면체의 부피를 만들어낸다는 것이다.
즉, 스칼라 삼중곱은 다음과 같은 성질을 가진다.
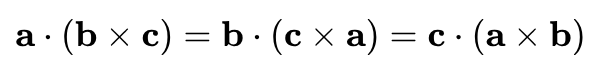
스칼라 삼중곱은 3차원 공간에서 세 벡터가 모두 선형 독립의 관계를 가지는지 판단하는 판별식으로 사용할 수 있다.
만약, 스칼라 삼중곱 값이 0이면, 어떤 두 벡터가 선형 종속이거나 어떤 두 벡터가 만드는 평면에 다른 벡터가 속하는 경우이다.
따라서 스칼라 삼중곱이 0이 아니면 세 벡터는 모두 선형 독립의 관계를 가짐을 알 수 있다.
2. 벡터 삼중곱
v x (u x w)
세 벡터의 외적으로 구성된 삼중곱에 대해서 알아보자.
벡터 삼중곱은 다음과 같은 성질을 지닌다.
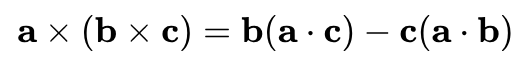
이를 삼중곱 전개 도는 라그랑주 공식이라고 한다.
이는 특별한 증명이 필요한 것은 아니고, 전개해서 정리하면 된다.
벡터 삼중곱은 다소 복잡한 외적은 두 개의 내적 연산으로 변환한다는 특징을 지닌다.
이 식의 우변은 결국 mb - nc 꼴 이므롤 벡터 삼중곱으로 만들어지는 벡터는 두 벡터 b, c 가 만드는 평면에 속함을 알 수 있다.
6. 연습문제
1. 다음 코드의 빈칸을 완성하시오

[문제코드]
#include <iostream>
using namespace std;
class Vector3D
{
public:
Vector3D()
: x(0.f), y(0.f), z(0.f) {}
Vector3D(float x, float y, float z)
: x(x), y(y), z(z) {}
Vector3D operator+(const Vector3D& other) const
{
return Vector3D(x + other.x, y + other.y, z + other.z);
}
Vector3D operator-(const Vector3D& other) const
{
return Vector3D(x - other.x, y - other.y, z - other.z);
}
Vector3D operator*(float scalar) const
{
return Vector3D(x * scalar, y * scalar, z * scalar);
}
float DotProduct(const Vector3D& other) const
{
/* 내적 */
}
Vector3D CrossProduct(const Vector3D& other) const
{
/* 외적 */
}
Vector3D VectorTripleProuct(const Vector3D& vector1, const Vector3D& vector2) const
{
/* 벡터 삼중곱 */
}
float ScalarTripleProduct(const Vector3D& vector1, const Vector3D& vector2) const
{
/* 스칼라 삼중곱 */
}
float GetLengthSquare() const
{
return x * x + y * y + z * z;
}
float GetLength() const
{
return sqrtf(GetLengthSquare());
}
void Nomalize()
{
float leng = GetLength();
if (leng == 0.f)
return;
x = x / leng;
y = y / leng;
z = z / leng;
}
Vector3D GetNomalizedVector() const
{
float leng = GetLength();
if (leng == 0.f)
return *this;
Vector3D returnVec = *this;
returnVec.x = x / leng;
returnVec.y = y / leng;
returnVec.z = z / leng;
return returnVec;
}
friend std::ostream& operator<<(std::ostream& os, const Vector3D& vec)
{
static const unsigned int BUFFER_MAX = 256;
char buffer[BUFFER_MAX] = {};
sprintf_s(buffer, BUFFER_MAX, "(%.2f, %.2f, %.2f)", vec.x, vec.y, vec.z);
os << buffer;
return os;
}
private:
float x, y, z;
};
int main()
{
}
[정답코드]
#include <iostream>
using namespace std;
class Vector3D
{
public:
Vector3D()
: x(0.f), y(0.f), z(0.f) {}
Vector3D(float x, float y, float z)
: x(x), y(y), z(z) {}
Vector3D operator+(const Vector3D& other) const
{
return Vector3D(x + other.x, y + other.y, z + other.z);
}
Vector3D operator-(const Vector3D& other) const
{
return Vector3D(x - other.x, y - other.y, z - other.z);
}
Vector3D operator*(float scalar) const
{
return Vector3D(x * scalar, y * scalar, z * scalar);
}
float DotProduct(const Vector3D& other) const
{
return x * other.x + y * other.y + z * other.z;
}
Vector3D CrossProduct(const Vector3D& other) const
{
Vector3D rstVector = {};
rstVector.x = (y * other.z - z * other.y);
rstVector.y = -x * other.z + z * other.x;
rstVector.z = (x * other.y - y * other.x);
return rstVector;
}
Vector3D VectorTripleProuct(const Vector3D& vector1, const Vector3D& vector2)const
{
Vector3D returnVec = {};
returnVec = vector1 * (this->DotProduct(vector2)) - vector2 * (this->DotProduct(vector1));
return returnVec;
}
float ScalarTripleProduct(const Vector3D& vector1, const Vector3D& vector2)const
{
return this->DotProduct(vector1.CrossProduct(vector2));
}
float GetLengthSquare()const
{
return x * x + y * y + z * z;
}
float GetLength()const
{
return sqrtf(GetLengthSquare());
}
void Nomalize()
{
float leng = GetLength();
if (leng == 0.f)
return;
x = x / leng;
y = y / leng;
z = z / leng;
}
Vector3D GetNomalizedVector() const
{
float leng = GetLength();
if (leng == 0.f)
return *this;
Vector3D returnVec = *this;
returnVec.x = x / leng;
returnVec.y = y / leng;
returnVec.z = z / leng;
return returnVec;
}
friend std::ostream& operator<<(std::ostream& os, const Vector3D& vec)
{
static const unsigned int BUFFER_MAX = 256;
char buffer[BUFFER_MAX] = {};
sprintf_s(buffer, BUFFER_MAX, "(%.2f, %.2f, %.2f)", vec.x, vec.y, vec.z);
os << buffer;
return os;
}
private:
float x, y, z;
};
int main()
{
}
2. 벡터 외적의 크기가 sin 에 비례하는 이유는 무엇인가?
3. 빈칸을 채우시오.
| 행렬곱 | 내적 | 외적 | |
| 계산 결과 | |||
| 교환법칙 | |||
| 결합법칙 | |||
| 덧셈에 대한 분배법칙 |
4. 크기가 다른 평행한 벡터 v와 u가 있다고 할 때, 이 두 벡터의 외적이 영벡터인 이유가 무엇인가?
5. 렌더링 최적화를 위해서, 시선에 감지되는 삼각형만 그리는 방법을 백페이스 컬링의 알고리즘이라고 한다.
어떤 삼각형을 만드는 세 점이 정의되어 있다고 하자. (세 점이 차례대로 정의된다.)
카메라는 (0, 0, 0)에 위치하고 뒤집어지지 않은 채로 (1, 1, 1) 을 바라보고 있다고 할 때,
해당 삼각형이 전면인지 후면인지 판별하시오
(1)
--------------------------
P1 (-1, 1, 1)
P2 (3, 1, 3)
P3 (-3, 2, 5)
--------------------------
(2)
--------------------------
P1 (-12,32,1)
P2 (4,271,9)
P3 (0,-12,18)
--------------------------
(3)
--------------------------
P1 (293.-123,-3)
P2 (81,-2391,1285)
P3 (-28,-234,75)
--------------------------
6. 로드리게스 회전 공식이 어떤 방식으로 짐벌락 현상을 해결하는지 쓰고, 최종 공식을 쓰시오
7. 아래는 스칼라 삼중곱의 성질이다. 스칼라 삼중곱이 아래와 같은 성질을 만족시키는 이유는 무엇인가?
또, 스칼라 삼중곱은 3차원 세계에서 서로 다른 벡터들의 선형성을 판별하는데 사용될 수 있는데, 이떻게 선형성을 판별할 수 있는지 설명하시오.
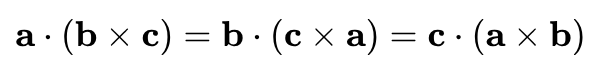
8. 3차원 공간에 두 점 v, u가 있다고 하자.
v = (3, 2, 5)
u = (2, 7, 3)
벡터 v, u가 만드는 평면에 존재하면서 벡터 u와 직교하는 2개의 벡터 w1와 w2의 정규화 벡터 구하여라.
'컴퓨터 그래픽스 > 수학' 카테고리의 다른 글
| [수학] 절두체 : 최적화된 3차원 공간 (0) | 2024.07.21 |
|---|---|
| [수학] 원근 투영: 화면에 현실감을 부여하는 변환 (11) | 2024.07.20 |
| [수학] 3차원 공간: 입체 공간의 생성 (3) | 2024.07.19 |
| [수학] 삼각형: 물체를 구성하는 가장 작은 단위 (0) | 2024.07.12 |
| [수학] 내적: 벡터 공간의 분석과 응용 (0) | 2024.07.11 |