📕 비트 연산자의 개념
비트 연산은 '2진수' 연산을 뜻하는데, 특정 연산자를 이용해서
이진 수로 표현된 정수에 대하여 논리적인 연산을 수행합니다.
2진수 연산은 10진수 연산에 익숙한 사람에겐 매우 생소한 개념일 수밖에 없습니다.
그러나, 컴퓨터와 같은 기계장치들의 근간은 2진수의 집합으로 이루어져 있기에
비트 연산을 사용하면, 컴퓨터 입장에서 매우 빠르게 연산할 수 있게 됩니다.
게임과 같은 매 프레임 반복적인 연산을 필요로 하는 프로그램을 개발할 때
단순한 곱셈이나 비교 연산을 비트 연산으로 치환해 주면 최적화하는데 도움이 될 수 있습니다.
📗 C++에서의 비트 연산자
1. &
AND 연산입니다.
피연산자가 모두 1(참) 일 경우 결괏값은 참이 됩니다.
| A | B | A&B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2. |
OR 연산입니다.
어떤 피연산자가 1(참) 일 경우 결괏값은 참이 됩니다.
| A | B | A|B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
3. ^
XOR 연산입니다.
두 피연산자가 다른 값을 가지고 있을 경우 결괏값은 참이 됩니다.
| A | B | A^B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XOR 연산을 처음 봤을 땐, 이런 논리 연산을 어디에 사용하는지 의문이 생겼는데
생각보다 다양하게 사용됩니다.
예를 들어, 피연산자 A와 B가 같은지를 비교할 때
A와 B의 모든 비트를 XOR 연산을 한 뒤
결과 비트에 대해 OR연산을 한 결괏값이
1이면 A와 B는 같지 않다.
0이면 A와 B는 같다고 판단할 수 있습니다.
그 외에도 암호학에서 '키 스트림 암호' 알고리즘에도 XOR 연산이 사용됩니다.
4. ~
NOT 연산입니다.
피연산자의 비트를 반전시킵니다.
| A | ~A |
| 0 | 1 |
| 0 | 0 |
~연산과 AND, OR, XOR 등의 연산을 결합하여
다양한 논리 연산을 만들 수 있습니다.
5. <<
왼쪽 시프트 연산입니다.
A = 0000 1001이라는 2진수 정수가 있을 때
A << 1 은
A<<1 = 001 0010 이 됩니다.
단순하게 모든 비트를 왼쪽으로 밀었다고 보시면 됩니다.
잘 생각해 보면, '왼쪽으로 1비트 시프트'는 '곱하기 2'와 동일한 의미를 가진다는 것을 알 수 있습니다.
6. >>
오른쪽 시프트 연산입니다.
왼쪽 시프트 연산과 방향만 오른쪽일 뿐 완전히 동일하게 동작합니다.
'오른쪽으로 1비트 시프트'는 '나누기 2'와 동일한 의미를 가집니다. (나머지는 고려하지 않음)
📘 비트 연산자를 이용하여 빠르게 홀수와 짝수 판단하기
홀수는 맨 오른쪽 비트(LSB)가 무조건 1이고
짝수는 맨 오른쪽 비트가 무조건 0입니다.
이것을 이용하여 기존 나머지 연산 보면 훨씬 빠르게 홀수와 짝수를 판단할 수 있습니다.
임의의 정수 a가 있을 때, a와 1을 AND 연산을 수행할 때,
홀수면 결과 값으로 1이
짝수면 결과 값으로 0이
나올 것 입니다.
1. 나머지 연산을 이용하여 홀수와 짝수 판단
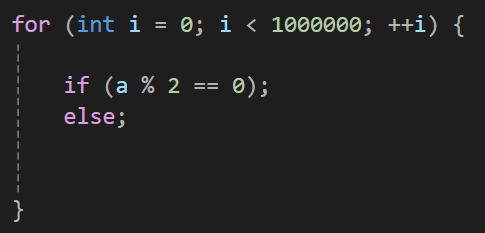
제 컴퓨터 환경에서 위 코드 수행에 452 ms가 소모되었습니다.
2. 비트 연산을 이용하여 홀수와 짝수 판단

제 컴퓨터 환경에서 위 코드 수행에 306 ms가 소모되었습니다.
📕 결론
비트 연산은 기본적인 사칙연산(+, -, /, *, % 등..) 보다 빠릅니다.
그렇기에 반복해서 연산해야할 것이 있는 경우 비트 연산을 사용하면 최적화에 도움이 될 것입니다.
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [C++/이론] 그래프 개론 (1) | 2024.01.04 |
|---|---|
| [ C++/알고리즘] 그리디 알고리즘 (Greedy Algorithm) (4) | 2023.12.26 |
| [C++/알고리즘] 퀵 정렬 (Quick Sort) (0) | 2023.12.25 |
| [C++/알고리즘] 분할정복 (Divide and Conquer) + 병합정렬 (Merge Sort) (0) | 2023.12.25 |
| [C++] 비둘기집 원리와 응용 (0) | 2023.12.24 |