개발하는 리프터 꽃게맨입니다.
[C++/알고리즘] 퀵 정렬 (Quick Sort) 본문
참고: https://powerclabman.tistory.com/12
[C++/알고리즘] 분할정복 (Divide and Conquer) + 병합정렬 (Merge Sort)
📕 개요 '분할 정복 알고리즘'이란, 엄청나게 크고 방대한 문제를 해결할 수 있는 단위까지 쪼개서 해결한 다음 그것들을 다시 합쳐서 원래의 문제를 해결하고자 하는 알고리즘 기법입니다. 그
powerclabman.tistory.com
📕 개요
퀵 정렬 또한 '분할정복 알고리즘' 기법을 사용해서 빠르게 배열을 정렬하는 알고리즘입니다.
먼저, 퀵 정렬의 아이디어부터 한 번 살펴보도록 합시다.

1. 피벗(Pivot)을 정합니다.
피벗은 임의의 '기준'을 뜻합니다.
2. 피벗을 기준으로 피벗 왼쪽에는 '피벗 보다 작은 값'을 두고, 피벗 오른쪽에는 '피벗 보다 큰 값'을 둡니다.
이것이 퀵 정렬의 핵심이며, 분할하는 방법입니다.
이렇게 피벗을 기준으로 '파티션'이 2개 생기죠
그러면 '파티션'에 대해서 '퀵 정렬'을 재귀적으로 수행하면 됩니다.
이제 이것을 '분할 정복 알고리즘'의 시점으로 다시 바라보겠습니다.
1. 분할
피벗을 정하고, 피벗 왼쪽엔 피벗보다 작은 값을
피벗 오른쪽엔 피벗보다 큰 값을 배치합니다.
그러면 피벗을 기준으로 파티션이 2개 생기고,
재귀적으로 파티션을 계속 분할합니다.
2. 정복
사이즈 1의 배열까지 분할한다면 정렬된 배열을 얻을 수 있으므로
정복할 수 있습니다.
3. 조합
병합 정렬과 달리 따로 조합하지 않아도 됩니다.
분할만 잘하면, 최종적으로 정렬된 배열을 얻을 수 있습니다.
📘 퀵 정렬의 특징
1. 대부분의 경우에서 모든 정렬 알고리즘 중에 가장 빠르다.
퀵정렬의 평균 시간 복잡도는 O(n log n)이며
최악의 경우 O(n^2) 이긴 하지만, 최적화 알고리즘을 통해 어느 정도 해소할 수 있습니다.
퀵 정렬의 최대 장점은 다른 O(n log n)의 정렬 알고리즘보다
대부분의 경우 더욱 빠르다는 것이 있습니다.
2. 불안정(Unstable) 정렬이다.
퀵 정렬은 정렬 시 원본의 순서를 보장하지 않는 불안정 정렬입니다.
그렇기에 '안정성'이 필요 없는 경우 퀵 정렬의 사용을 고려할 수 있습니다.
3. 병합 정렬에 비해 공간 복잡도가 우수하다.
병합 정렬은 병합 단계에서 임시적인 배열을 사용하기에 추가적인 메모리가 필요합니다.
(자세한 정보는 위 '참고 링크' 확인)
그러나 퀵 정렬은 병합 정렬과 달리 추가 공간이 필요하지 않기에, 메모리를 좀 더 효율적으로 사용할 수 있습니다.
📗 구현
1. 시작
#define MAX 100
int main()
{
int arr[MAX] = { 10, 5, 2, 0, 7, 8, 4, 6 };
int size = 8;
return 0;
}
위 정수 배열 arr를 '퀵 정렬'로 정렬해 보겠습니다.
2. 분할
먼저 피벗 값을 고르고, 피벗을 기준으로
피벗의 왼쪽에는 피벗보다 작은 값들이,
피벗의 오른쪽에는 피벗보다 큰 값들이 오도록 하는 함수를 구현해 보도록 하겠습니다.
아이디어는 다음과 같습니다.
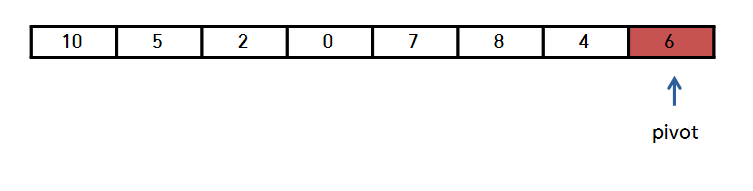
구현시 편의상 '로무토 파티션' 기법으로 코딩하겠습니다.
(로무토 파티션을 기억해 주세요, 나중에 한 번 더 다루겠습니다.)
먼저, 맨 오른쪽 값을 '피벗'으로 설정합니다.
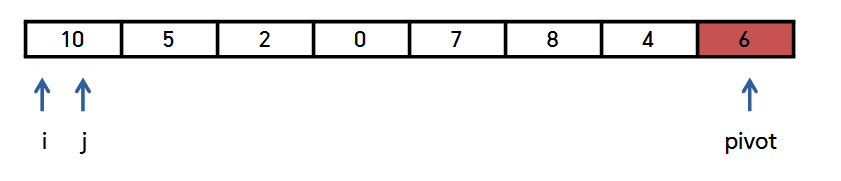
맨 왼쪽부터 인덱스를 가리키는 i, j를 설정합니다.
j는 한 칸씩 오른쪽으로 이동하면서, '피봇'보다 '작은 값'을 발견하면
arr [i]와 arr [j]을 바꿔줄 것입니다.
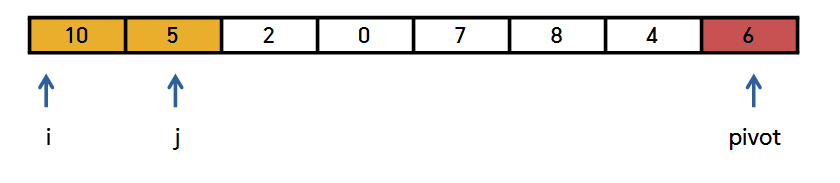
이런 식으로 j 값에 있는 원소가 '피벗' 보다 작으면
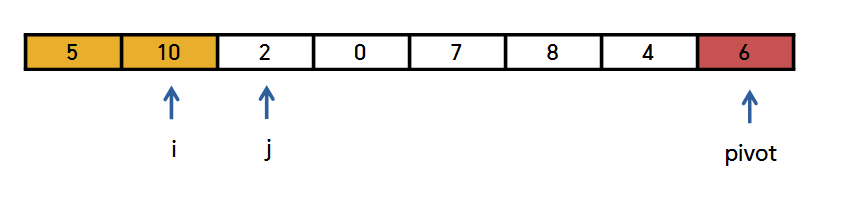
이런 식으로 Swap을 발생시키고
둘 다 오른쪽으로 한 칸씩 이동합니다.
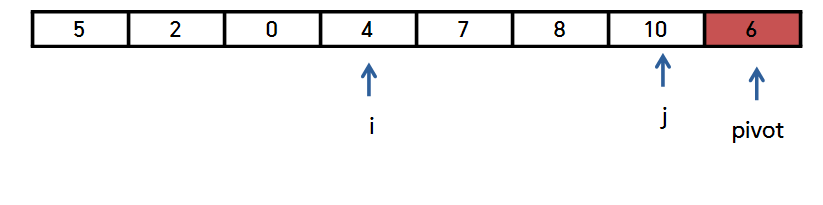
최종적으로 이렇게 될 것이고,
i+1과 pivot을 바꿔주면, 파티션을 나눌 수 있습니다.

피봇을 기준으로 왼쪽에는 작은 값
오른쪽에는 큰 값이 위치해 있죠?
이러면 분할의 구현은 된 겁니다.
이제 왼쪽 파티션과 오른쪽 파티션에 대해서 재귀적으로 퀵 정렬을 해주면
완성입니다.
먼저 '파티션'을 구분하는 함수는 다음과 같습니다.
void swap(int& a, int& b)
{
int temp = a;
a = b;
b = temp;
}
int Partition(int* arr, int start, int end)
{
int pivot = arr[end];
int i = start-1;
for (int j = start; j < end; j++)
{
if (arr[j] < pivot)
{
i++;
swap(arr[j], arr[i]);
}
}
swap(arr[i+1], arr[end]);
return i+1;
}
이것이 파티션을 만드는 함수이고 아래 코드가
계속해서 분할하는 코드입니다.
void QuickSort(int* arr, int start, int end)
{
if (start < end)
{
int pivot = Partition(arr, start, end);
QuickSort(arr, start, pivot - 1);
QuickSort(arr, pivot + 1, end);
}
}pivot이 존재하는 인덱스를 받아서
그것을 기준으로 왼쪽 파티션, 오른쪽 파티션에 대해서
재귀적으로 퀵 정렬을 수행합니다.
5. 코드 완성 및 전체 코드
#include <iostream>
#define MAX 100
using namespace std;
void swap(int& a, int& b)
{
int temp = a;
a = b;
b = temp;
}
int Partition(int* arr, int start, int end)
{
int pivot = arr[end];
int i = start;
for (int j = start; j < end; j++)
{
if (arr[j] < pivot)
{
swap(arr[j], arr[i]);
i++;
}
}
swap(arr[i], arr[end]);
return i;
}
void QuickSort(int* arr, int start, int end)
{
if (start < end)
{
int pivot = Partition(arr, start, end);
QuickSort(arr, start, pivot - 1);
QuickSort(arr, pivot + 1, end);
}
}
int main()
{
int arr[MAX] = { 10, 5, 2, 0, 7, 8, 4, 6 };
int size = 8;
QuickSort(arr, 0, size - 1);
return 0;
}
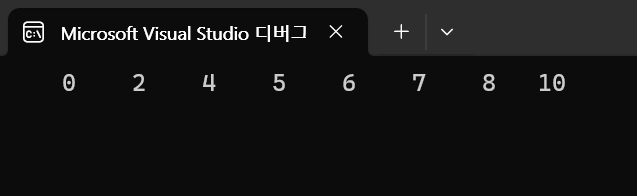
정렬 결과입니다.

배열의 사이즈를 더 키워서 정렬을 해보았습니다.
매우 잘됩니다.
🎈 마치며
제가 소개한 '퀵 정렬'은 퀵 정렬 중에서도 성능이 좋지 않습니다.
(물론, 평균적인 성능이 O(n log n) 이기에 매우 빠른 알고리즘에 속합니다.)
저는 '로무토 파티션'이라는 알고리즘으로 퀵 정렬을 구현했는데,
로무토 파티션의 경우 구현 난이도는 낮지만
교환이 너무나 잦고, 피벗이 어떻게 선택되냐에 따라서
최악의 경우 O(n^2)의 복잡도를 보입니다.
그래서 위 알고리즘은 꼭 최적화가 필요합니다.
고려해 볼 사항은 다음과 같습니다.
1. 파티션을 어떻게 나누는가?
어떻게 하면 교환을 적게 하면서 파티션을 나누는 것이 좋을까?
2. 피벗을 어떻게 설정하는 것이 좋은가?
아무래도 중앙값에 가까운 피벗을 선택할수록 교환이 적게 일어나기에
성능이 좋아질 가능성이 높습니다.
추가적으로, 퀵 정렬은 평균적인 상황에서 최고 속도를 보여줍니다.
그러나, 특정 상황에서 다른 정렬 알고리즘보다 독보적으로 빠른 정렬 알고리즘이 있는데
그것은 '삽입 정렬'입니다.
퀵 정렬과 삽입 정렬을 어느 정도 섞어서 사용하면 최적의 성능을 이끌어낼 수 있지 않을까요?
다음에 시간이 난다면 포스팅해 보겠습니다.
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [C++/이론] 그래프 개론 (1) | 2024.01.04 |
|---|---|
| [ C++/알고리즘] 그리디 알고리즘 (Greedy Algorithm) (4) | 2023.12.26 |
| [C++/알고리즘] 분할정복 (Divide and Conquer) + 병합정렬 (Merge Sort) (0) | 2023.12.25 |
| [C++] 비둘기집 원리와 응용 (0) | 2023.12.24 |
| [C++] Bitwise Operator와 빠른 홀수, 짝수 찾기 (3) | 2023.12.23 |



