📕 개요
'분할 정복 알고리즘'이란, 엄청나게 크고 방대한 문제를 해결할 수 있는 단위까지
쪼개서 해결한 다음 그것들을 다시 합쳐서 원래의 문제를 해결하고자 하는 알고리즘 기법입니다.
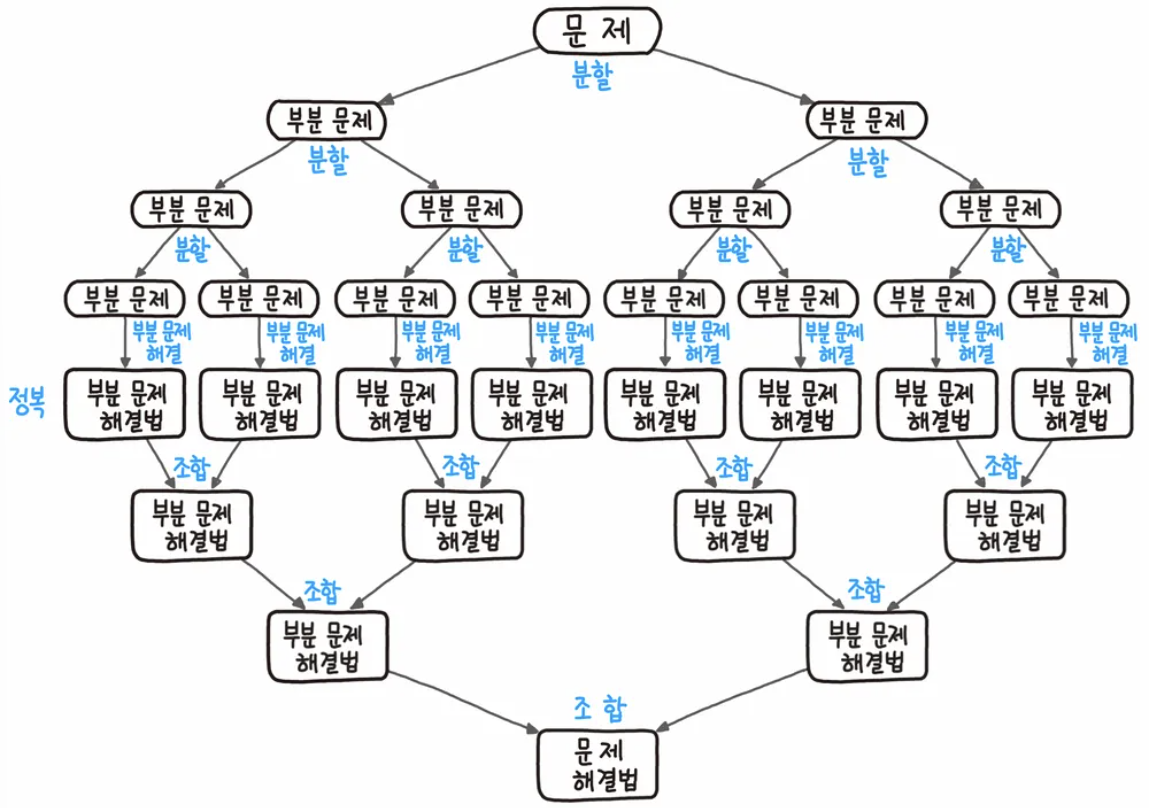
그림처럼 '큰 문제'를 '부분 문제'로 계속해서 분할합니다.
그리고 '부분 문제'를 해결하고, 해답을 조합하여서
원래 문제에 대한 해답을 얻어 내고자 하는 것이 이 알고리즘의 핵심입니다.
논리는 다음과 같습니다.
1. 분할 (Divide)
큰 문제를 매우 작은 부분 문제로 분할합니다.
2. 정복 (Conquer)
가장 작은 단위의 부분 문제를 해결합니다.
3. 조합 (Combine)
하위 문제에 대한 결과를 조합하여, 원래 문제의 답을 얻어 냅니다.
분할 정복법은 대부분 '재귀' 로 구현됩니다.
다음은 분할 정복 알고리즘으로 해결할 수 있는 대표적인 문제인
'병합 정렬'에 대해서 알아봅니다.
📘 병합정렬?

위 그림이 '병합 정렬'의 알고리즘을 도식화한 것입니다.
기본적인 논리 자체는 '분할 정복 알고리즘'과 동일합니다.
1. 분할
N개의 비정렬 상태의 배열이 있을 때,
정렬 상태를 만들기 위해 '부분 배열'로 계속해서 분할한다.
최종적으로 크기가 1인 배열이 나올 때까지 계속해서 분할한다.
2. 정복
크기가 1인 배열에 대해서 정렬을 수행한다.
여기서, 크기가 1인 배열은 '항상 정렬된 상태'를 유지하기에
정복은 됐다고 표현할 수 있습니다.
3. 조합
이제 정렬된 부분 배열을 합쳐서 더 큰 부분 배열을 만들 것인데
조합한 배열도 정렬된 상태를 유지해야 하기에,
정렬된 새로운 부분 배열을 만드는 로직을 구현해야 합니다.
최종 조합을 끝마쳤을 때는 완성된 배열이 나올 것입니다.
📗 병합정렬의 특징
1. 속도가 매우 빠르다.
병합정렬의 시간 복잡도는 O(nlogn)으로 정렬 알고리즘 중에서는
퀵 정렬(Quick Sort)과 비슷한 수준의 속도를 보여줍니다.
퀵 정렬은 최악의 경우 O(n^2)의 복잡도를 보이지만
병합정렬은 일관적으로 O(nlogn)의 복잡도를 가집니다.
2. 안정(Stable) 정렬이다.
퀵 정렬의 경우는 '순서'를 보장하지 않는 정렬 알고리즘이지만,
병합 정렬은 '순서'를 보장합니다.
안정성이란 동일한 요소의 원래 순서를 보장한다는 의미로 다음 그림을 보면 이해하기 쉽습니다.
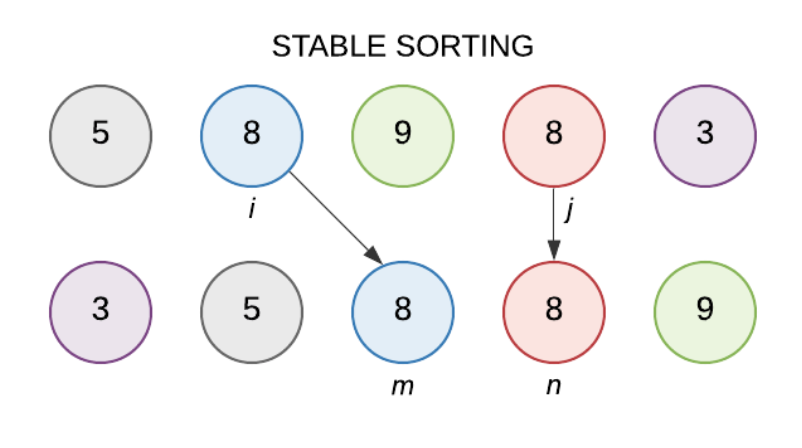
같은 8이지만
안정성을 보장하지 않는 알고리즘의 경우 '파란 8'과 '붉은 8'의 순서를 보장하지 않지만 (ex. 선택 정렬, 퀵 정렬)
안정성을 보장하는 알고리즘의 경우 두 개의 순서를 보장합니다. (ex. 병합 정렬, 삽입 정렬)
📕 구현
1. 시작
// define MAX 100
int main()
{
int arr[MAX] = { 1,8,5,3,2,6,43,21,12,37 };
int size = 10;
return 0;
}
위 정수 배열 arr를 '병합 정렬'로 정렬해 보겠습니다.
2. 분할
먼저 arr 배열을 사이즈 1의 배열로 분할해 줄 것이며,
이때 재귀를 사용합니다.
void MergeSort(int* arr, int start, int end)
{
if (start < end)
{
int mid = (start + end) / 2;
MergeSort(arr, start, mid);
MergeSort(arr, mid + 1, end);
}
}
MergeSort 함수가 재귀적으로 실행되면서
arr배열을 반으로 계속 분할합니다.
start == end 인 순간은 사이즈가 1이라는 뜻이기에
조건을 if(start < end)로 잡아줬습니다

대충 이런 느낌으로 계속 분할되는 코드입니다.
3. 정복
사이즈가 1인 배열까지 분할을 완료했다면, 이미 정복은 끝난 것 입니다.
사이즈가 1인 배열에서는 어떤 수가 존재하더라도 이미 정렬된 상태이기에
'정렬'이라는 문제를 해결한 것이죠.
이제 조합만 잘하면 됩니다.
4. 조합

이렇게 생각하면 편합니다.
'임의의 정렬된 두 배열 A, B를 하나의 정렬로 만들자!'
이것이 병합정렬 '조합 단계'의 핵심 로직입니다.

'left 배열'의 첫번째 인덱스를 left, 마지막을 mid
'right 배열'의 첫번째 인덱스를 mid+1, 마지막을 end
라고 했을 때
새로운 배열을 하나 만들어서
처음부터 하나씩 채워가는 로직을 만들어 봅니다.
int sorted[MAX];
int index = 0;
int left = start;
int right = mid+1;
while (left <= mid && right <= end)
{
if (arr[left] < arr[right])
{
sorted[index++] = arr[left++];
}
else
sorted[index++] = arr[right++];
}
이런 식으로, 새로운 배열 sorted를 선언하여
sorted의 처음 인덱스부터 하나하나씩 원소를 채워갈 것인데,
left배열과 right배열의 값을 비교하여서 정렬된 상태로
채워나가면 되겠습니다.
(지금 코드가 이해가 잘 안가실 수도 있는데 전체 코드를 보면 아마 조금 감이 잡힐 겁니다.)
while (left <= mid)
sorted[index++] = arr[left++];
while (right <= end)
sorted[index++] = arr[right++];
for (int i = 0; i < index; i++)
arr[start + i] = sorted[i];그리고 미처 다 넣지 못한 left배열과 right배열의 남은 원소들을
sorted 배열에 다 넣어주면 되는 것이죠.
그러면 정렬된 부분 배열인 sorted 배열이 완성됩니다.
그리고 이제 sorted 배열을 원본 배열 arr에 순서에 맞게 삽입해주면 조합 끝입니다.
다음은 '조합'의 전체 코드입니다.
void Merge(int* arr, int start, int mid, int end)
{
int sorted[MAX];
int index = 0;
int left = start;
int right = mid+1;
while (left <= mid && right <= end)
{
if (arr[left] < arr[right])
sorted[index++] = arr[left++];
else
sorted[index++] = arr[right++];
}
while (left <= mid)
sorted[index++] = arr[left++];
while (right <= end)
sorted[index++] = arr[right++];
for (int i = 0; i < index; i++)
arr[start + i] = sorted[i];
}
5. 코드 완성 및 전체 코드
#include <iostream>
#define MAX 100
using namespace std;
void Merge(int* arr, int start, int mid, int end)
{
int sorted[MAX];
int index = 0;
int left = start;
int right = mid+1;
while (left <= mid && right <= end)
{
if (arr[left] < arr[right])
sorted[index++] = arr[left++];
else
sorted[index++] = arr[right++];
}
while (left <= mid)
sorted[index++] = arr[left++];
while (right <= end)
sorted[index++] = arr[right++];
for (int i = 0; i < index; i++)
arr[start + i] = sorted[i];
}
void MergeSort(int* arr, int start, int end)
{
if (start < end)
{
int mid = (start + end) / 2;
MergeSort(arr, start, mid);
MergeSort(arr, mid + 1, end);
Merge(arr, start, mid, end);
}
}
int main()
{
int arr[MAX] = { 1,8,5,3,2,6,43,21,12,37 };
int size = 10;
MergeSort(arr, 0, size - 1);
return 0;
}

정렬 결과 입니다.

배열의 사이즈를 조금 키워봤습니다.
정렬이 매우 잘됩니다.
🎈 마치며
저는 개인적으로 알고리즘에 재귀가 들어가면 항상 머릿속이 복잡해집니다.
그래도 문제 해결에 있어서 매우 유용한 기법이니 꼭 많은 연습 해보시길 추천드립니다.
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [C++/이론] 그래프 개론 (1) | 2024.01.04 |
|---|---|
| [ C++/알고리즘] 그리디 알고리즘 (Greedy Algorithm) (4) | 2023.12.26 |
| [C++/알고리즘] 퀵 정렬 (Quick Sort) (0) | 2023.12.25 |
| [C++] 비둘기집 원리와 응용 (0) | 2023.12.24 |
| [C++] Bitwise Operator와 빠른 홀수, 짝수 찾기 (3) | 2023.12.23 |