(참고: 기본적인 구현인 '인접 행렬'을 사용해서 구현했습니다.)
서론
탐색은 우리가 관리하는 자료구조의 전체를 순회하거나 원하는 자료를 찾고자 하는 것을 뜻합니다.
자료구조를 다루는 시점에서 '탐색'은 필수적이죠.
그런데, 그래프 구조는 복잡하기에 단순하게 순회하는 것조차 힘듭니다.
일반적으로 탐색의 방법은
'깊이 우선 탐색 DFS'
'너비 우선 탐색 BFS'
2가지가 존재합니다.
깊이 우선 탐색
1. 개요

깊이 우선 탐색은 말 그대로
출발점에서 가장 멀리 있는 노드(가장 깊이 있는 노드)를 도달하고자 하는 탐색방법입니다.
A에서 가장 멀리 있는 노드는 F죠
그래서 A -> D -> F를 먼저 탐색하고
나머지 노드를 탐색합니다.
이런 식으로 탐색하는 이유는 '스택'의 특성 때문에 그렇습니다.
알고리즘의 의사 코드를 살펴보면서 추가적으로 말해보겠습니다.
2. 의사코드
visited 배열이 존재하고, 이 배열은 해당 정점에 방문했는가를 bool 형으로 체크한다.
BFS(정점) :
visited[정점] = true
for(자신과 연결된 다른 정점 탐색)
if(만약 해당 정점이 방문되지 않았다면)
BFS(다음 정점)
BFS는 기본적으로 자기 자신을 호출하는 '재귀 함수' 형태입니다.
- 먼저 시작 정점을 매개 변수로 넘긴 뒤에
- 시작 정점을 방문했다고 visited에 표시하고
- 자신과 연결된 다른 정점을 탐색하고
- 탐색한 정점이 visited에 false로 표시되어 있으면
- 그 정점으로 간다.
라는 논리 구조를 가지고 있습니다.
3. 코드
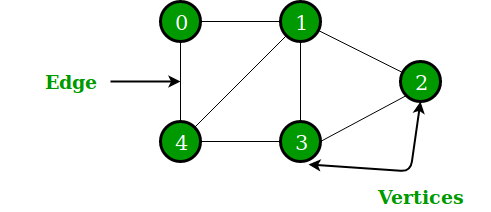
아래 코드에는 위 그래프를 구현하였으며
정점 0을 기준으로 DFS를 수행하였습니다.
void DFS(Graph& g, int here, vector<bool>& visited)
{
//vistied 를 넘겨줘도 되고
//전역변수로 사용해도 상관없습니다.
cout << here << " -> ";
visited[here] = true;
for (int there = 0; there < g._vertex; there++)
{
if (visited[there] == false && g._adjacent[here][there] == true)
DFS(g, there, visited);
}
}

<전체 코드>
#include <iostream>
#include <vector>
using namespace std;
class Graph
{
public:
Graph(int v)
: _vertex(v)
{
_adjacent = vector<vector<bool>>(_vertex, vector<bool>(_vertex, false));
}
void CreateEdge(int from, int to)
{
//무방향 그래프임을 가정
_adjacent[from][to] = true;
_adjacent[to][from] = true;
}
public:
int _vertex;
vector<vector<bool>> _adjacent;
};
void DFS(Graph& g, int here, vector<bool>& visited)
{
//vistied 를 넘겨줘도 되고
//전역변수로 사용해도 상관없습니다.
cout << here << " -> ";
visited[here] = true;
for (int there = 0; there < g._vertex; there++)
{
if (visited[there] == false && g._adjacent[here][there] == true)
DFS(g, there, visited);
}
}
int main()
{
const int VERTEX_CNT = 5;
Graph g(VERTEX_CNT);
g.CreateEdge(0, 1);
g.CreateEdge(0, 4);
g.CreateEdge(1, 2);
g.CreateEdge(1, 3);
g.CreateEdge(1, 4);
g.CreateEdge(2, 3);
g.CreateEdge(3, 4);
vector<bool> visited(g._vertex, false);
DFS(g, 0, visited);
}DFS는 재귀함수이기에 일단 발견한 노드로 가고, 또 탐색하고
발견했으면 또 이동하고, 탐색하고.. 를 반복하고
최대 깊이에 도달했으면 오는 과정에서 발견한 노드를 마저 방문하면서 탐색을 끝마칩니다.
그래서 '깊이 우선 탐색'인 것입니다.
재귀는 함수 호출의 오버헤드가 있기 때문에
스택 자료구조를 사용하여 최적화할 수 있습니다.
<스택 최적화 코드>
visited 로 방문했음을 표시하는 것이 아니라
discovered 로 발견했다고 표시한다.
void DFS_stack(Graph& g, int start)
{
stack<int> st;
vector<bool> discovered(g._vertex, false);
discovered[start] = true;
st.push(start);
while (!st.empty())
{
int here = st.top();
st.pop();
cout << here << " -> ";
for (int there = g._vertex - 1; there >= 0; there--)
{
if (discovered[there] == false && g._adjacent[here][there] == true)
{
st.push(there);
discovered[there] = true;
}
}
}
}
깊이 우선 탐색은 n개의 노드와 e개의 간선을 탐색하므로
인접리스트의 경우 O(n+e)의 시간 복잡도를
인접행렬의 경우 O(n^2)의 시간 복잡도를 가집니다.
간선이 많이 존재하지 않는 경우 인접 리스트를 사용하는 것이 좋습니다.
너비 우선 탐색
1. 개요
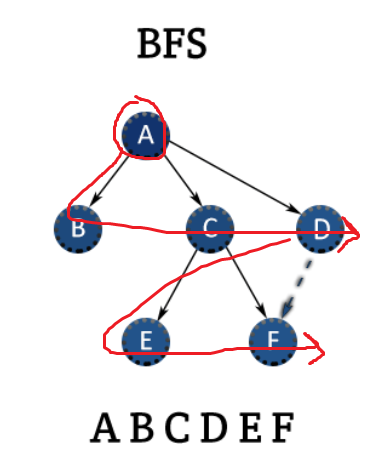
너비 우선 탐색은 깊이 우선 탐색과 반대로
출발점과 가까이 있는 노드 먼저 싹 다 탐색을 하고
그다음 거리에 있는 노드를 탐색합니다.
A에서 가장 가까이 있는 노드 B, C, D 먼저 탐색을 한 뒤에
그 다음 거리에 있는 E, F를 탐색합니다.
DFS에서 핵심은 '큐'입니다.
현재 노드에서 모든 노드를 발견해서 우선적으로 '큐'에 넣어둡니다.
알고리즘의 의사 코드를 살펴보면서 추가적으로 말해보겠습니다.
2. 의사코드
discovered 배열이 존재하고, 이 배열은 '정점'을 발견했는가? 를 표시하는 역할을 한다.
DFS(출발정점) :
발견한 정점을 저장하는 큐 Q 생성
discovered[정점]에 방문했다고 표시
while(Q가 빌때까지 반복)
Q에서 정점을 꺼내서
for (연결된 모든 정점을 찾는다.)
if(dicovered[정점]에 방문을 하지 않았다면)
Q에 발견한 정점 삽입
discovered[정점]에 발견했다고 표시
DFS는 발견한 노드를 큐에 다 넣어놓고 큐 front에 있는 정점을 방문하는 형태입니다.
- 먼저 시작 정점을 매개 변수로 넘긴 뒤에
- 시작 정점을 발견했다고 discovered에 표시하고
- 자신과 연결된 다른 정점을 탐색하고
- 탐색한 정점이 discovered에 false로 표시되어 있으면
- 발견한 정점은 모두 큐에 넣는다.
- 그다음 큐에 저장된 정점 하나를 빼서, 큐가 빌 때까지 반복한다.
라는 논리 구조를 가지고 있습니다.
3. 코드

아래 코드에는 위 그래프를 구현하였으며
정점 0을 기준으로 BFS를 수행하였습니다.
void BFS(Graph& g, int start)
{
vector<bool> discovered(g._vertex, false);
queue<int> q;
discovered[start] = true;
q.push(start);
while (!q.empty())
{
int here = q.front();
q.pop();
cout << here << " -> ";
for (int there = 0; there < g._vertex; there++)
{
if (discovered[there] == true)
continue;
if (g._adjacent[here][there] == false)
continue;
q.push(there);
discovered[there] = true;
}
}
}

<전체 코드>
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
class Graph
{
public:
Graph(int v)
: _vertex(v)
{
_adjacent = vector<vector<bool>>(_vertex, vector<bool>(_vertex, false));
}
void CreateEdge(int from, int to)
{
//무방향 그래프임을 가정
_adjacent[from][to] = true;
_adjacent[to][from] = true;
}
public:
int _vertex;
vector<vector<bool>> _adjacent;
};
void BFS(Graph& g, int start)
{
vector<bool> discovered(g._vertex, false);
queue<int> q;
discovered[start] = true;
q.push(start);
while (!q.empty())
{
int here = q.front();
q.pop();
cout << here << " -> ";
for (int there = 0; there < g._vertex; there++)
{
if (discovered[there] == true)
continue;
if (g._adjacent[here][there] == false)
continue;
q.push(there);
discovered[there] = true;
}
}
}
int main()
{
const int VERTEX_CNT = 5;
Graph g(VERTEX_CNT);
g.CreateEdge(0, 1);
g.CreateEdge(0, 4);
g.CreateEdge(1, 2);
g.CreateEdge(1, 3);
g.CreateEdge(1, 4);
g.CreateEdge(2, 3);
g.CreateEdge(3, 4);
BFS(g, 0);
}BFS는 큐에 넣어놓고 큐에서 빼서 먼저 발견한 노드부터
차례로 탐색하기 때문에, 거리가 가까운 노드부터 탐색할 수 있습니다.
그래서 '너비 우선 탐색'인 것입니다.
너비 우선 탐색 역시
인접리스트의 경우 O(n+e)의 시간 복잡도를
인접행렬의 경우 O(n^2)의 시간 복잡도를 가집니다.
마치며
그래프는 현실 세계의 데이터 구조와 매우 가깝기 때문에 굉장히 유용한데 반해, 단순하게 순회 및 탐색만 해도 알고리즘이 생각보다 복잡해집니다.
이제 조금 더 나아가서, 이런 탐색 알고리즘은 어떤 식으로 확장할 수 있을까요?
그리고 이때까지는 노드~노드 사이의 이동 비용이 없었는데, 이동 비용이 존재한다면 그리고 최소 이동 비용으로 탐색하려면 어떻게 해야 할까요?
다음 포스팅은
'경로 역추적: BFS을 이용한 미로 찾기 알고리즘
'최단 경로 알고리즘: 다익스트라 알고리즘'
'최단 경로 역추적: A* 알고리즘을 이용한 미로 찾기 알고리즘'
을 차례대로 다뤄보겠습니다.
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [C++/이론] 다익스트라 알고리즘 (Dijkstra Algorithm) (1) | 2024.01.04 |
|---|---|
| [C++] 경로 역추적: BFS을 이용한 '미로찾기 알고리즘' (2) | 2024.01.04 |
| [C++/이론] 그래프 개론 (1) | 2024.01.04 |
| [ C++/알고리즘] 그리디 알고리즘 (Greedy Algorithm) (4) | 2023.12.26 |
| [C++/알고리즘] 퀵 정렬 (Quick Sort) (0) | 2023.12.25 |