개발하는 리프터 꽃게맨입니다.
[DX11 물방울책 요약 정리] 챕터1: 벡터 대수 본문
파트1: 수학적 선수지식
비디오 게임은 가상 세계를 시뮬레이션하려고 시도한다. 하지만 컴퓨터는 그 본질상 숫자를 계산한다.
따라서 컴퓨터에 세계를 어떻게 전달할 것인가 하는 문제가 발생한다.
그 해답은 우리의 세계와 그 안의 상호작용을 완전히 수학적으로 기술하는 것이다.
따라서 수학은 비디오 게임 개발에서 기본적인 역할을 한다.
이 사전 요구사항 부분에서는 이 책 전반에 걸쳐 사용할 수학적 도구를 소개한다.
벡터, 좌표계, 행렬 및 변환에 중점을 두며, 이러한 도구들은 이 책의 거의 모든 샘플 프로그램에서 사용된다.
수학적 설명 외에도 XNA 수학 라이브러리에서 관련 클래스와 함수에 대한 데모가 제공된다.
여기서 다루는 주세는 이 책의 나머지 내용을 이해하는 데 필수적인 것들만 다루고 있으며, 이는 결코 비디오 게임 수학에 대한 포괄적인 내용을 설명하지 않는다.
챕터1, 벡터 대수: 벡터는 아마도 컴퓨터 게임에서 사용되는 가장 기본적인 수학적 객체일 것이다. 예를 들어, 벡터를 사용하여 위치, 변위, 방향, 속도, 힘 등을 나타낸다. 이 장에서는 벡터와 이를 조작하는 데 사용되는 연산에 대해 공부한다.
챕터2, 행렬 대수: 행렬은 변환을 표현하는 효율적이고 간결한 방법을 제공한다. 이 장에서는 행렬과 그에 정의된 연산에 익숙해진다.
챕터3, 변환: 이 장에서는 세 가지 기본 기하학적 변환, 크기변환, 회전변환, 평행 이동을 살펴본다. 이 변환들을 사용하여 공간에서 3D 객체를 조작한다.
또한, 한 좌표계에서 다른 좌표계로 좌표를 변환하는 데 사용되는 좌표 변환의 변경에 대해 설명한다.
제 1장: 벡터 대수
벡터는 컴퓨터 그래픽스, 충돌 감지 및 물리적 시뮬레이션에서 중요한 역할을 하며, 이는 모두 현대 비디오 게임의 일반적인 구성 요소이다.
여기서 엄밀하지 않고 실용성있게 접근합니다.
벡터는 이 책의 거의 모든 데모 프로그램에서 사용된다는 점을 강조합니다.
목표:
1. 벡터가 기하학적 및 수치적으로 어떻게 표현되는지 배우기.
2. 벡터에 정의된 연산과 그 기하학적 응용을 발견하기.
3. XNA Math 라이브러리의 벡터 함수와 클래스에 익숙해지기.
벡터
벡터는 크기와 방향을 모두 갖춘 양을 의미한다.
(책에 설명이 부실하여 의역 및 추가적인 설명이 존재함)
벡터에서는 크기와 방향에 대한 정보가 있으며, 벡터의 양으로 특정 방향으로 크기만큼 적용되는 힘, 입자가 이동한 순 방향과 거리를 나타내는 변위, 속력과 뱡향을 나타내는 속도 등을 나타낼 수 있다.
따라서 벡터는 힘, 변위 및 속도를 나타내닌 데 사용된다.
또한 벡터는 3D 게임에서 플레이어가 바라보는 방향, 폴리곤이 향하는 방향,빛의 방향, 빛이 표면에서 반사되는 방향과 같은 순수한 방향을 의미하기도 한다.
벡터를 수학적으로 정의하는 방법은 기하학적으로 표현하는 것이다. 방향이 있는 선분을 그려보자, 선분의 길이는 벡터의 크기를, 화살표의 방향은 벡터의 방향을 나타낸다.

벡터를 그리는 위치는 중요하지 않다. 위치를 변경해도 크기나 방향이라는 벡터의 속성을 변하지 않기 때문이다.
따라서 크기, 방향이 동일한 두 벡터는 동일한 벡터라고 말할 수 있다.
즉, 위 그림의 벡터 u와 v는 동일한 벡터임을 이해할 수 있다.
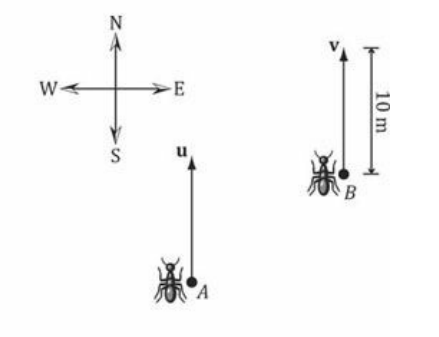
벡터 자체는 위치와 독립적인 양으로, 단순히 개미들이 그들이 있는 위치에서 어떻게 얼마나 움직일지를 지시하는 야에 불과하다.
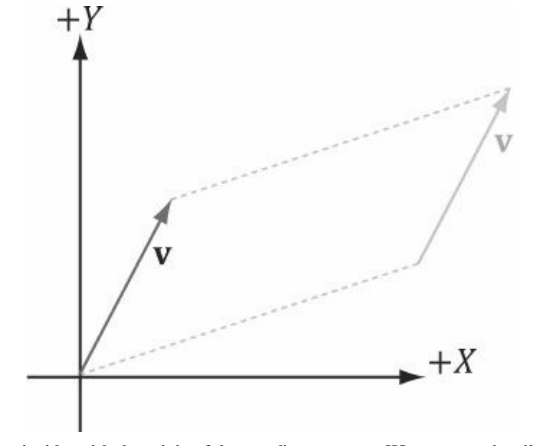
해당 책에서는 벡터의 시작을 꼬리 tail 벡터의 끝을 머리 head 라고 하는데, 벡터의 꼬리가 원점과 일치할 경우 이를 표준 위치에 있다고 한다.
좀 더 일반적인 표현으로 위치 벡터 position vector 라고 한다.
벡터와 좌표계 (Coordinate System)
벡터의 기하학적 의미를 어느정도 살펴봤기에, 이러한 의미를 컴퓨터에 적용시킬 수도 있을 것이다.
그러나 컴퓨터는 벡터를 기하학적으로 처리할 수 있기 때문에, 벡터를 수치적으로 지정하는 방법을 찾아야 한다.
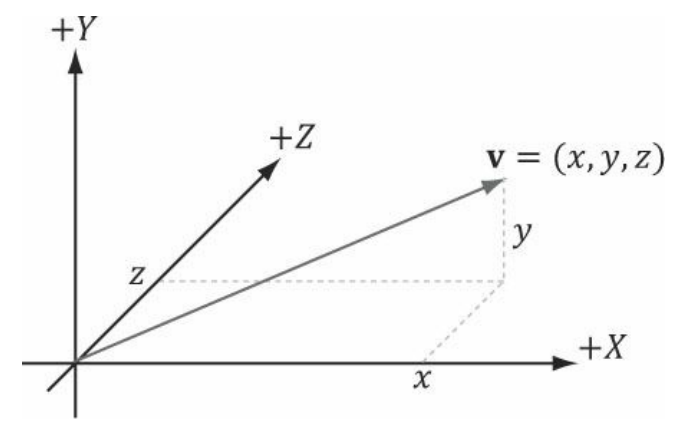
따라서, 우리는 공간에 3D 좌표계를 도입하고, 모든 벡터를 평행 이동하여 그들의 시작점이 원점과 일치하도록 한다.
(즉, 컴퓨터 그래픽스에서는 독자적은 3D 좌표계를 사용하고, 위치 벡터를 기본적으로 사용한다는 의미)
모든 벡터들의 시작점은 원점이므로, 끝점의 좌표 v = (x, y, z) 만 사용하여 벡터를 식별할 수 있다.
이제 벡터를 컴퓨터 프로그램에서 3개의 실수로 나타낼 수 있다.
(2D에서 작업할 경우 2D 좌표계와 2개의 실수로 나타낸다.)
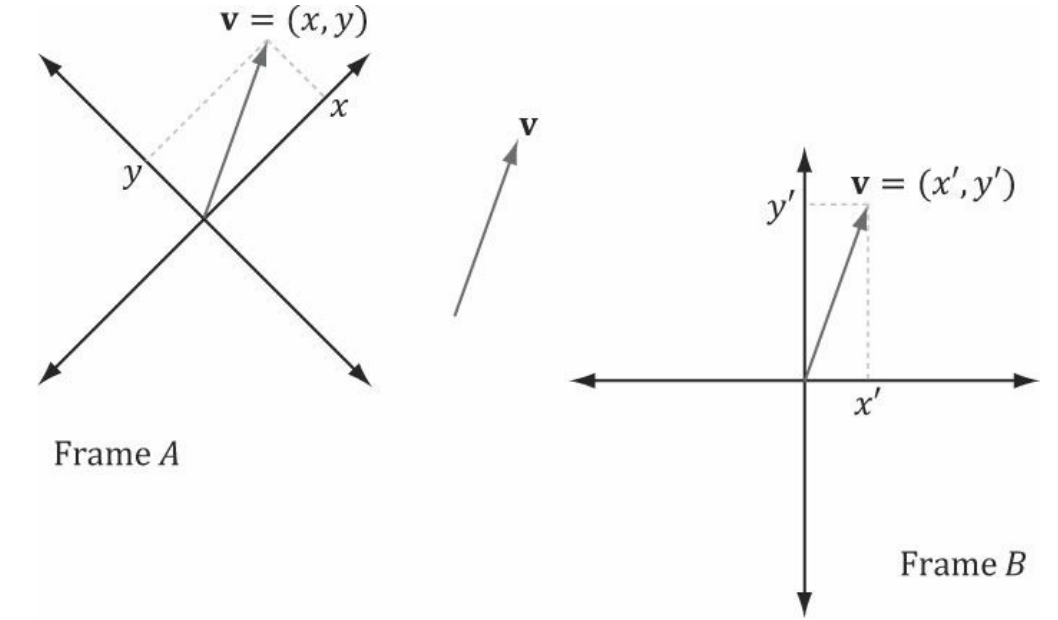
해당 그림을 보라.
이는 벡터 v와 서로 다른 기준 좌표계를 보여주고 있다.
이 그림이 보여주는 것은 좌표계를 어떻게 설정하냐에 따라서 동일한 벡터 v가 다른 좌표 표현을 가진다는 것이다.
이 개념은 온도와 유사하다. 물이 끓는점은 섭씨 표현에서는 100도, 화씨 표현에서는 212도이다.
물을 끓이는 물리적인 정도는 동일하지만, 어떤 단위를 쓰느냐에 따라서 표현이 달라질 수 있다.
마찬가지로, 벡터의 경우 방향과 크기는 변하지 않으나, 이를 설명하는 데 사용하는 기준 좌표계에 따라 좌표가 변할 수 있다.
이 점은 중요하다. 벡터를 좌표로 식별할 때, 그 좌표는 항상 특정 기준 좌표계에 상대적이라는 의미이기 때문이다.
컴퓨터 그래픽스에서는 여러 좌표계를 사용하며, 벡터의 좌표가 어떤 기준 좌표계에서 상대적인지를 추적해야 하며, 또한 벡터 좌표를 한 좌표계에서 다른 좌표계로 변환할 수 있어야 한다.
벡터와 점 모두 기준 좌표계에 상대적인 좌표 (x, y, z)에 대해서 설명될 수 있지만, 이 둘의 개념은 다르다.
벡터는 크기와 방향을 나타내는 반면, 점은 3차원 공간에서의 위치를 나타내는 개념이기 때문이다.
왼손 좌표계와 오른손 좌표계
DX3D는 소위 왼손 좌표계를 사용한다.
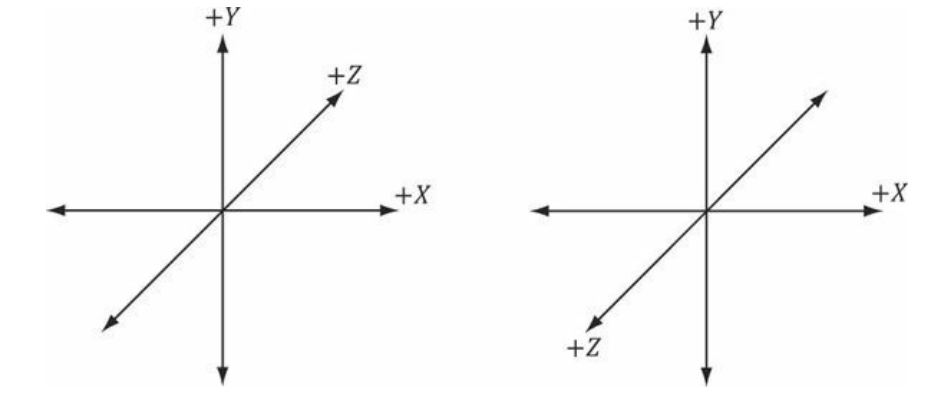
DX3D는 왼손 좌표계를 사용한다. 왼손을 사용하여 엄지를 X축, 검지를 Y축 방향으로 뻗으면 중지가 향하는 방향이 Z축이 된다. (책에서 말하는 방법이랑 다르지만, 이 방법이 더 직관적이기에 대체)
왼손 좌표계에서는 양의 z축이 모니터 뒷쪽으로 뻗어가고 오른손 좌표계에서는 양의 z축이 모니터 앞면으로 뻗어간다.
기본적인 벡터 연산
(너무 기본적인 내용이기에 축약)

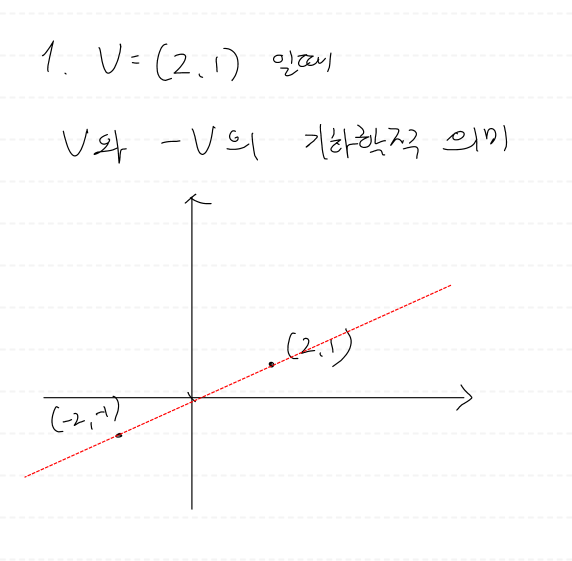
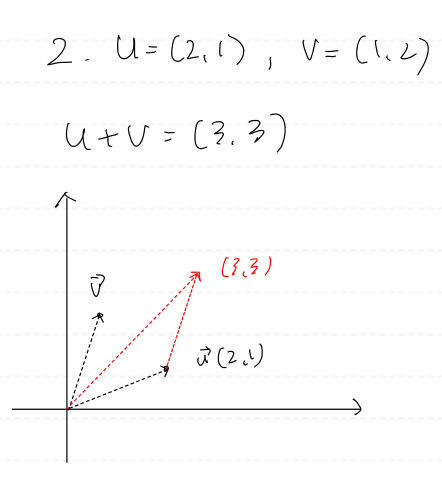
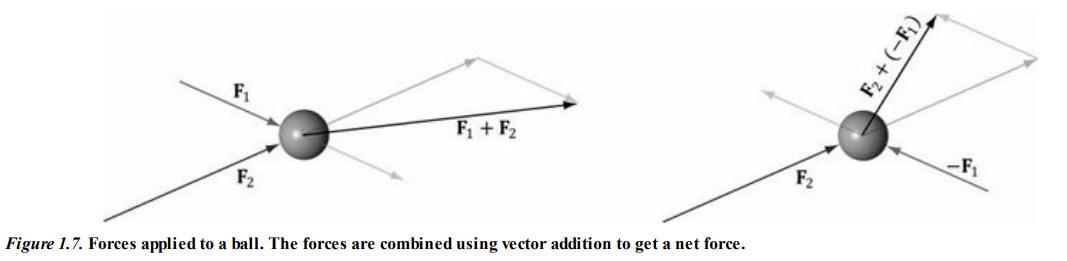
두 벡터의 합은 힘을 합하여 순수한 힘을
생성할 때 물리적으로 직관적으로 예상할 수 있는 결과와 일치한다.
두 벡터를 같은 방향으로 더하면 더 긴 벡터가 생성된다.
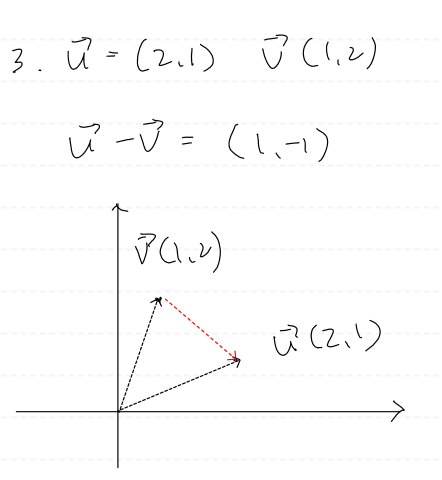
u - v는 점 v에서 점 u로 향하는 벡터를 제공한다.
(끝점에서 시작점을 빼서 구할 수 있다.)
벡터의 길이와 단위 벡터

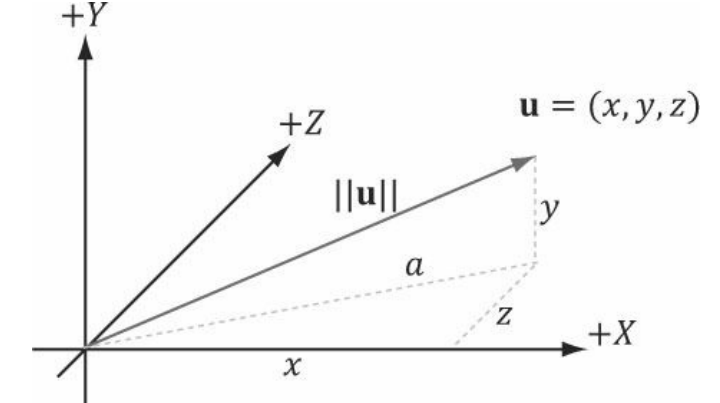
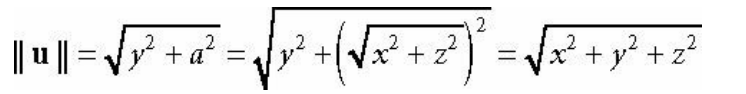
기하학적으로 벡터의 크기는 방향성 선분의 길이이다.
벡터의 크기는 두 개의 수직 막대로 나타낸다.
3D 벡터의 크기는 피타고라스 정리를 2번 적용하여 계산할 수 있다.
많은 경우에서 벡터의 길이 정보가 필요없고 방향성만 필요하다.
그렇기 때문에 벡터에서 방향 정보만 빼내는 방법을 생각해본다.
이러한 벡터를 단위 벡터, Unit Vector, 방향 벡터, 정규화 벡터 등으로 부르며, 이러한 벡터의 크기는 1이다.
어떤 벡터를 단위 벡터로 만들기 위해서는 벡터의 정규화라는 과정이 필요하다.
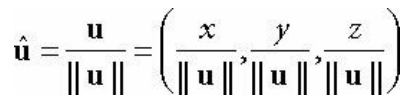
정규화는 각 성분의 벡터의 크기로 나누는 것을 의미한다.
단위 벡터에는 특별하게 단위 위에 hat을 씌워서 표기한다.
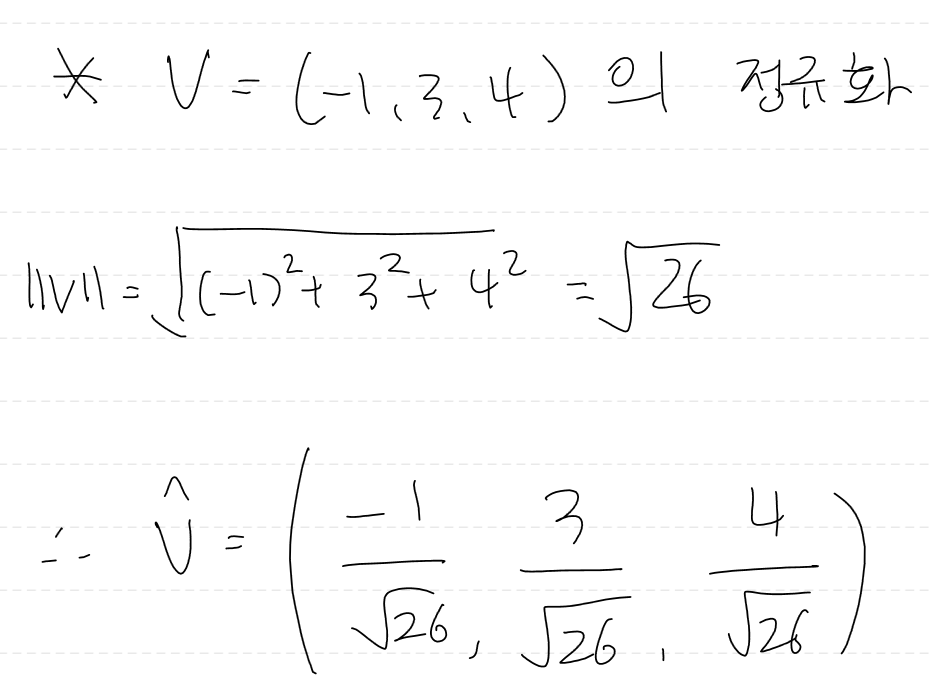
내적 Dot Product
내적은 벡터와 벡터 간의 연산으로 결과는 스칼라 값이 된다.
이 때문에 내적을 스칼라 곱이라고도 한다.
내적는 두 벡터의 요소들의 곱으로 정의된다.
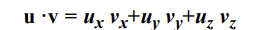
내적은 명확한 기하학적 의미를 제공하지는 않는다.
내적의 코사인 법칙을 사용하면 내적의 활용방안을 찾을 수 있다.
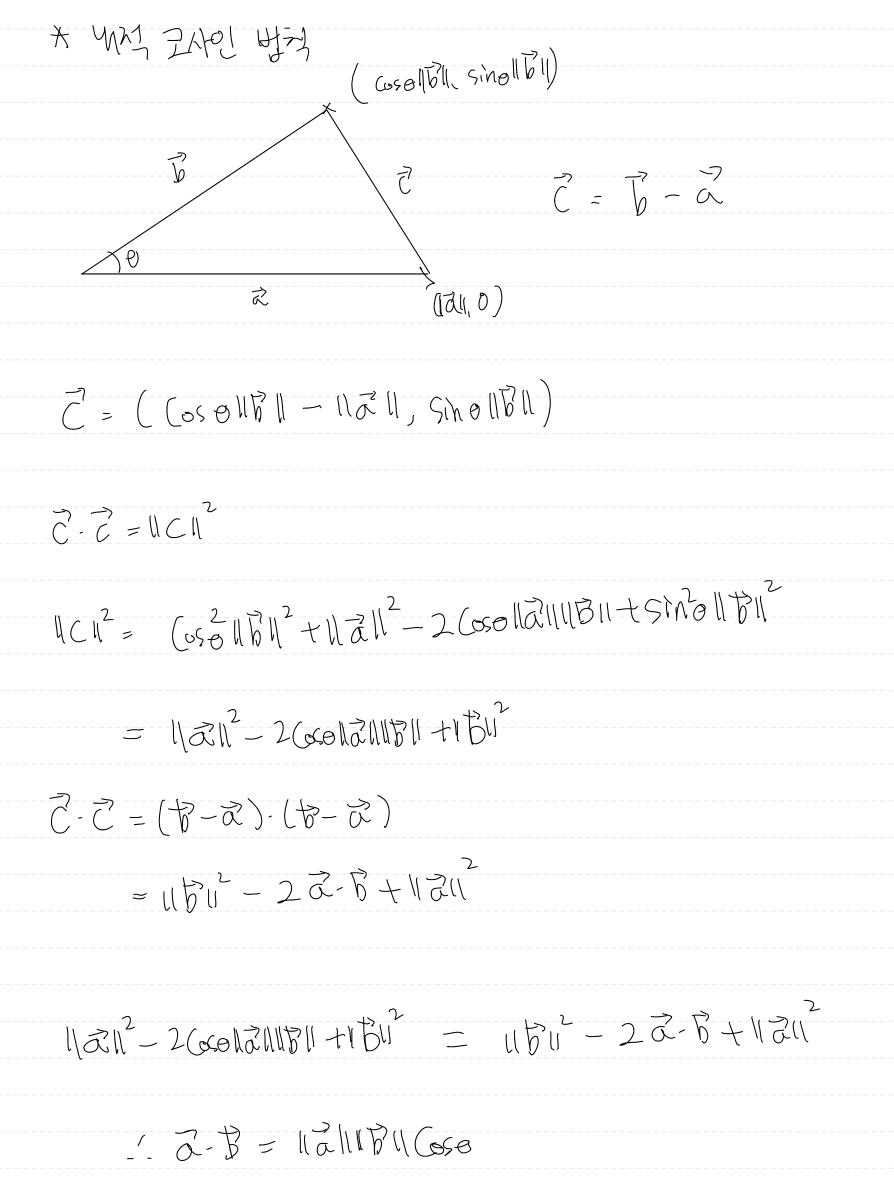
따라서 두 벡터 사이의 내적은 벡터들의 크기들과 코사인으로 표현할 수 있다.
특히, u와 v가 모두 단위 벡터일 경우 u와 v의 내적인 두 벡터의 사잇각의 코사인이 된다.
이제 내적이 제공하는 기하학적 성질을 이해할 수 있다.
두 벡터의 내적이 0이면, 두 벡터는 직교한다.
두 벡터의 내적이 양수면, 두 벡터의 사잇각은 예각이다. 두 벡터는 같은 방향을 향한다.
두 벡터의 내적이 음수면, 두 벡터의 사잇각은 둔각이다. 두 벡터는 반대 방향을 향한다.
문제) 벡터 v와 단위 벡터 n이 주어졌을 때, 내적을 사용하여 p에 대한 v와 n의 공식을 찾으십시오.
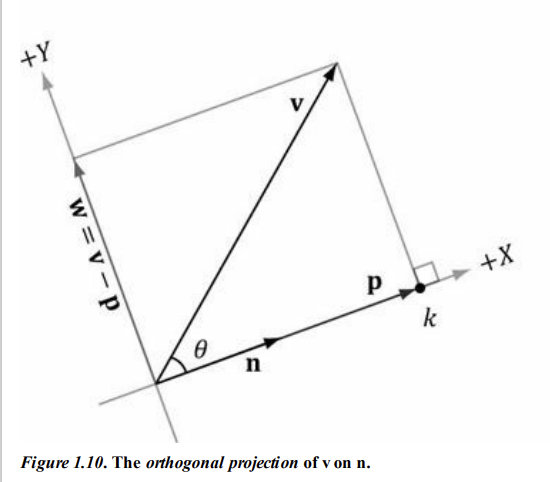

위 상황가 같은 경우
벡터 p는 벡터 v를 벡터 n에 대한 직교 투영이라고 부른다.

일반적으로 위와 같이 나타낸다.
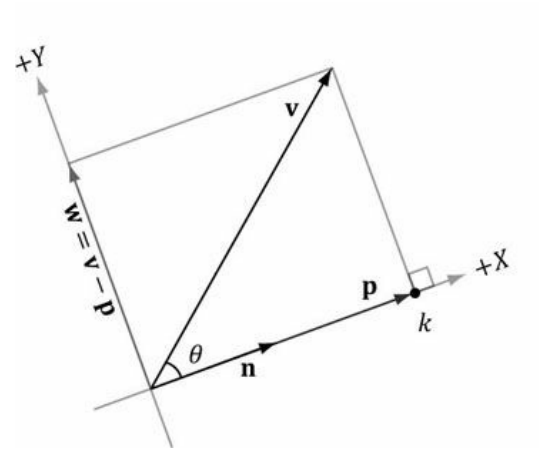
이를 역학적으로 해석해보자.
v를 힘으로 해석하면, p는 n으로 작용하는 힘 v의 일부로 생각할 수 있다.
그러면 p를 수평힘으로 볼 수 있는데, v - p를 이용하여 방향 n에 수직으로 작용하는 힘도 구할 수 있다.
이를 다음과 같이 표현한다.
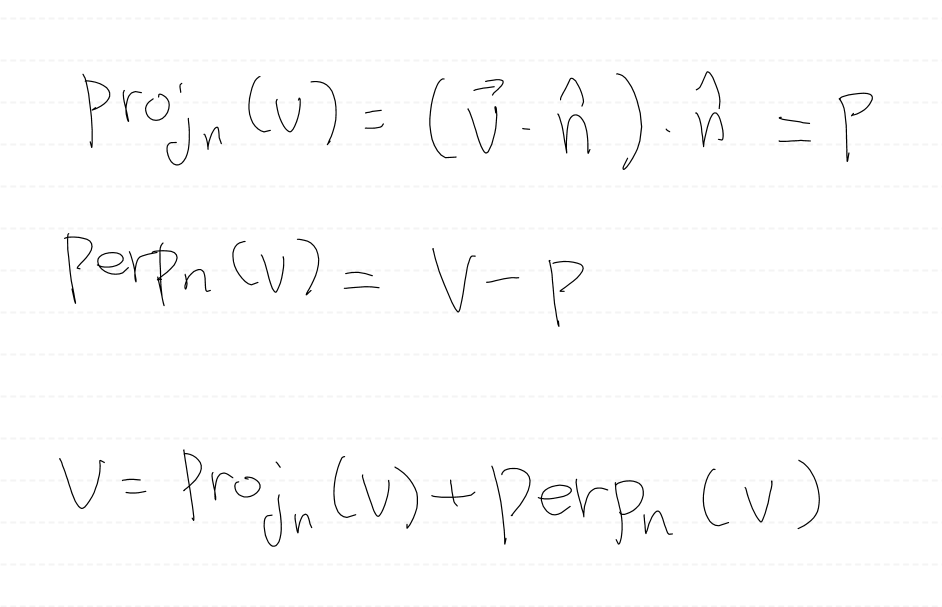
만약 n이 단위 벡터가 아니라면, 직교 투영 벡터 p를 구하는 공식은 다음과 같이 정의할 수 있다.
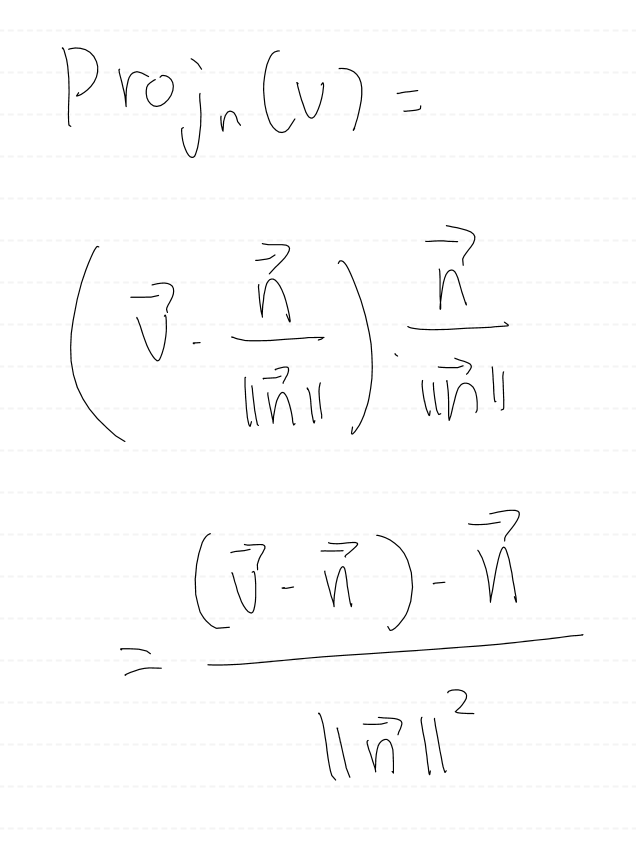
직교화 Orthogonalization

벡터 집합에 있는 모든 벡터들이 서로 직교하고 단위 벡터일 경우, 이를 정규 직교 집합이라고 한다.
컴퓨터 그래픽스에서는 일반적으로 정규 직교 집합으로 시작한다. 그러나 수치 정밀도의 문제로 인해 (float 의 정밀도..) 집합이 점차적으로 비정규 직교화될 수 있다.
그러므로 직교화란 어떤 집합을 정규 직교 집합으로 만드는 것을 의미한다.
먼저 2차원에서 직교화를 수행해보자.

이를 시각적으로 나타내보자.
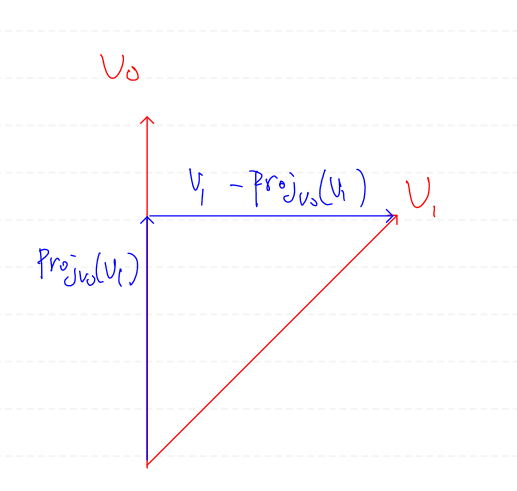
v0과 perp(v1)를 정규화하면 2차원 직교화를 수행할 수 있다.
3차원 직교화를 해보자.
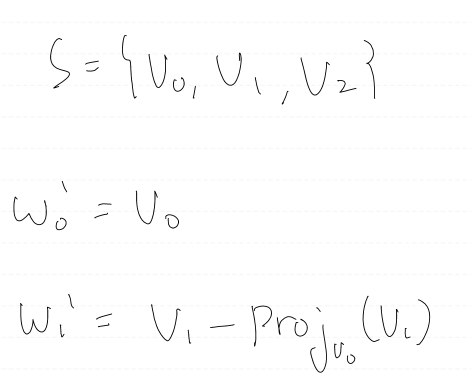
먼저 두 개의 벡터는 2D와 동일한 방식으로 구할 수 있고
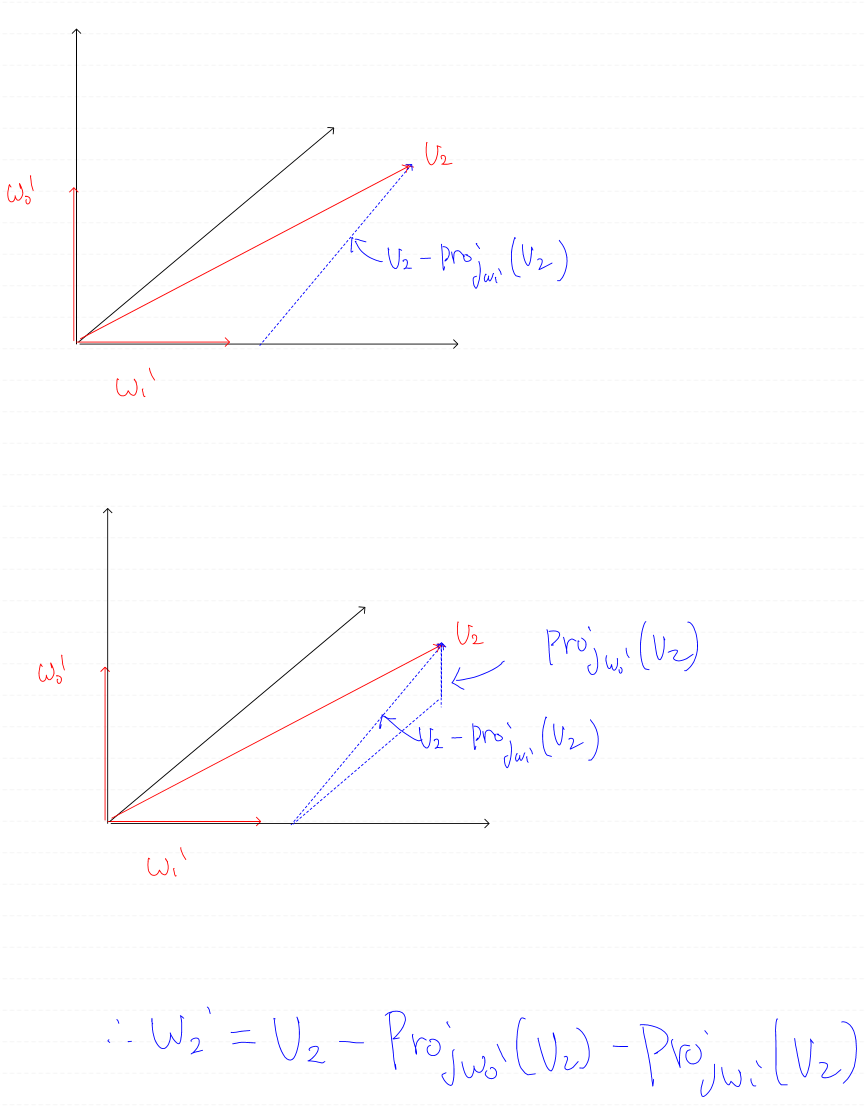
마지막 직교벡터는 두 직교 벡터에 직교 투영을 이용하여 구할 수 있다.
자세한 논리는 위 그림을 참고하라.
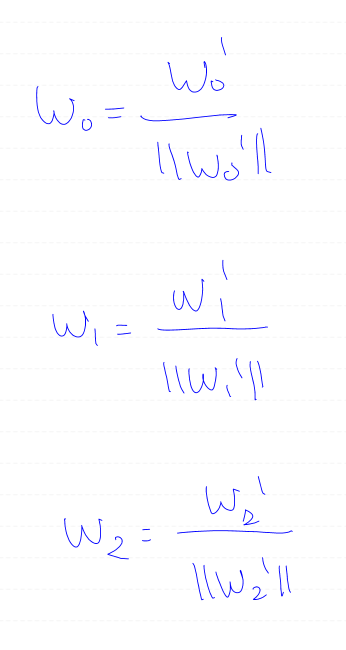
최종적으로 정규화를 수행하여 정규 직교 집합을 얻어낼 수 있다.
이러한 절차를 그램-슈미트 직교화 과정이라고 한다.
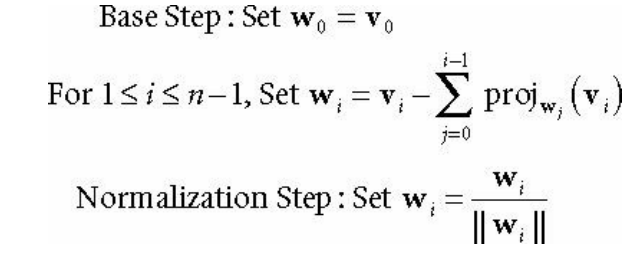
그램-슈미트 직교화 과정을 일반화하면 위와 같은 공식을 가진다.
이 식을 직관적으로 이해해보자.
이미 직교화된 벡터 집합 Wn = {w0, w1, w2, w3, ... , wn-1} 이 있다고 하자.
여기에 벡터 v를 추가한다고 할 때
w0 ~ wn-1 까지 벡터 v와 직교하는 성분을 구해 v에서 뺀다.
그 다음 정규화를 수행하면 정규 직교 집합을 유지할 수 있다.
벡터의 외적 Cross Product
벡터와 벡터 사이에 정의된 두 번째 연산이다.
벡터 외적의 결과는 벡터이다.
외적은 3차원 벡터에 대해서만 정의되며 2차원 외적은 존재하지 않는다.
두 3차원 벡터 u와 v가 외적을 취하면, u와 v에 모두 직교하는 벡터 w가 생성된다.
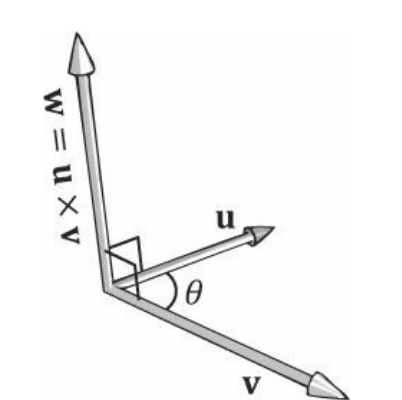
두 3D 벡터 u와 v를 외적하면 계산식은 다음과 같다.
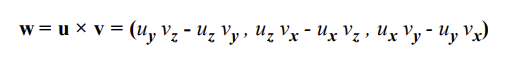
외적의 결과로 만들어지는 벡터를 구하려면, 손가락을 첫 번째 벡터방향으로 뻗은 뒤 두 번쨰 벡터방향으로 구부리면 된다. 다. 그러면 엄지가 가리키는 방향이 외적 결과 벡터가 된다. 이를 왼손법칙이라고 한다.
왼손 좌표계라 왼손을 사용하는 것이고 오른손 좌표계면 오른손을 사용한다.
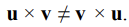
외적 식을 보면 알겠지만, 뺄쎔이 들어가 있으므로 교환법칙이 적용되지 않는다.
따라서 외적인 반교환적(aniti-commutative)라고 한다.
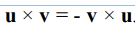
외적의 식을 잘 생각한다면 위와같은 식이 적용됨을 이해할 수 있다.
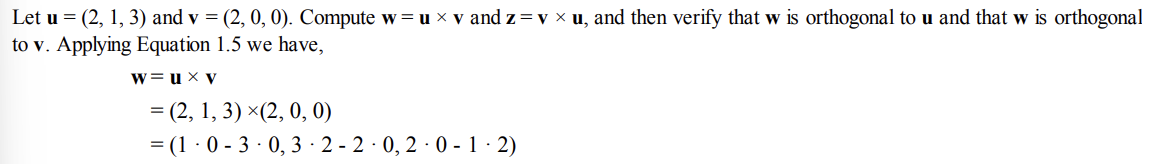
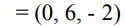
예제를 보자.
u = (2, 1, 3) 과 v = (2, 0, 0) 을 외적하면 두 벡터에 직교하는 벡터 (0, 6, -2)를 얻을 수 있다.
이 벡터가 진짜 두 벡터에 직교하는 벡터인지 살펴보기 위해서
w와 u의 내적, w와 v의 내적을 각각 구해보도록 한다.
만약, 정말고 직교한다면 두 값은 모두 0일 것이다.
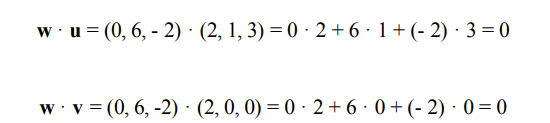
외적을 이용한 직교화
(앞서 의사 2D 외적이 존재했는데, 내용이 그닥이라 스킵함.)
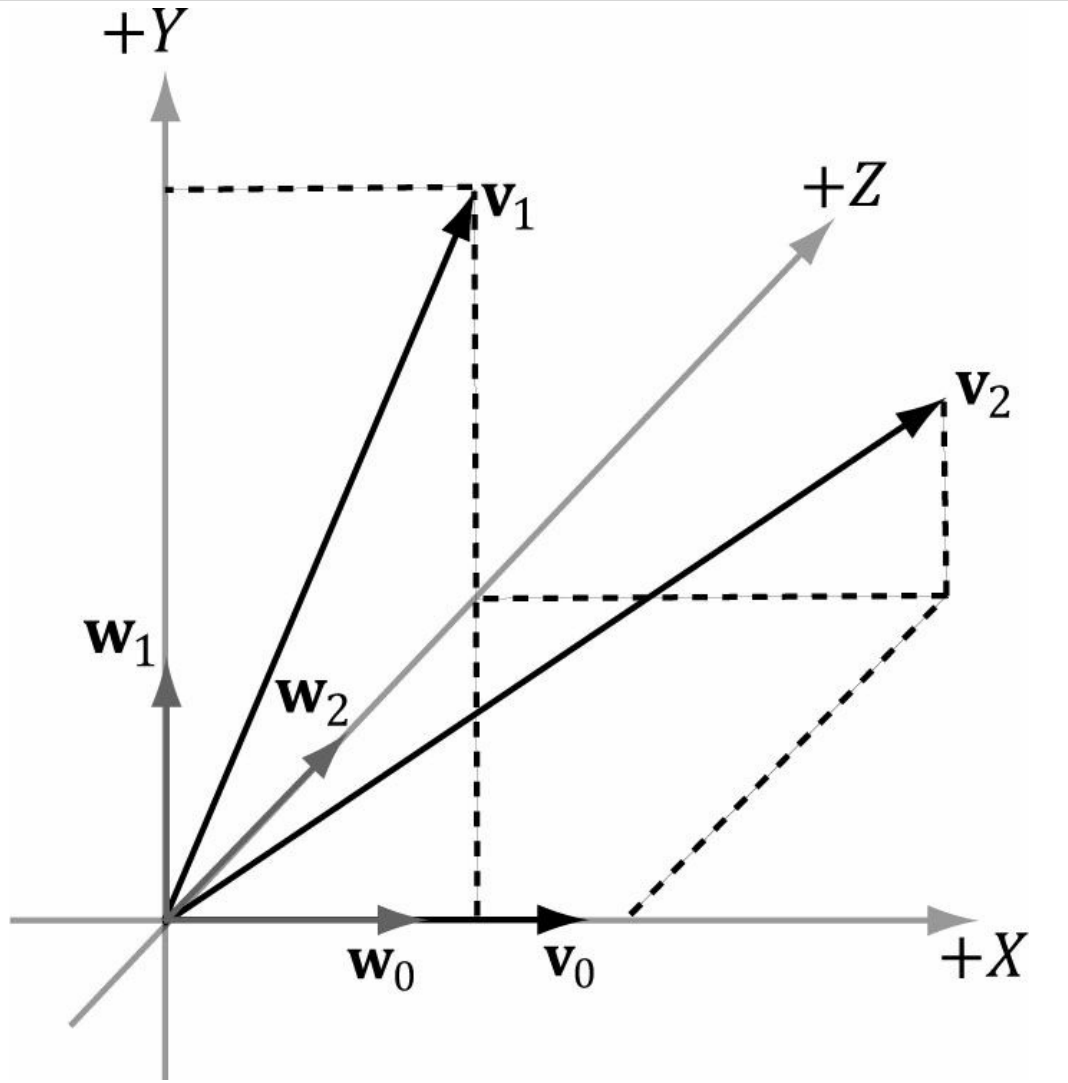
외적을 통해서 직교화하는 또다른 방법에 대해서 알아본다.
Sn = {v0, v1, v2} 가 존재한다고 할 때,
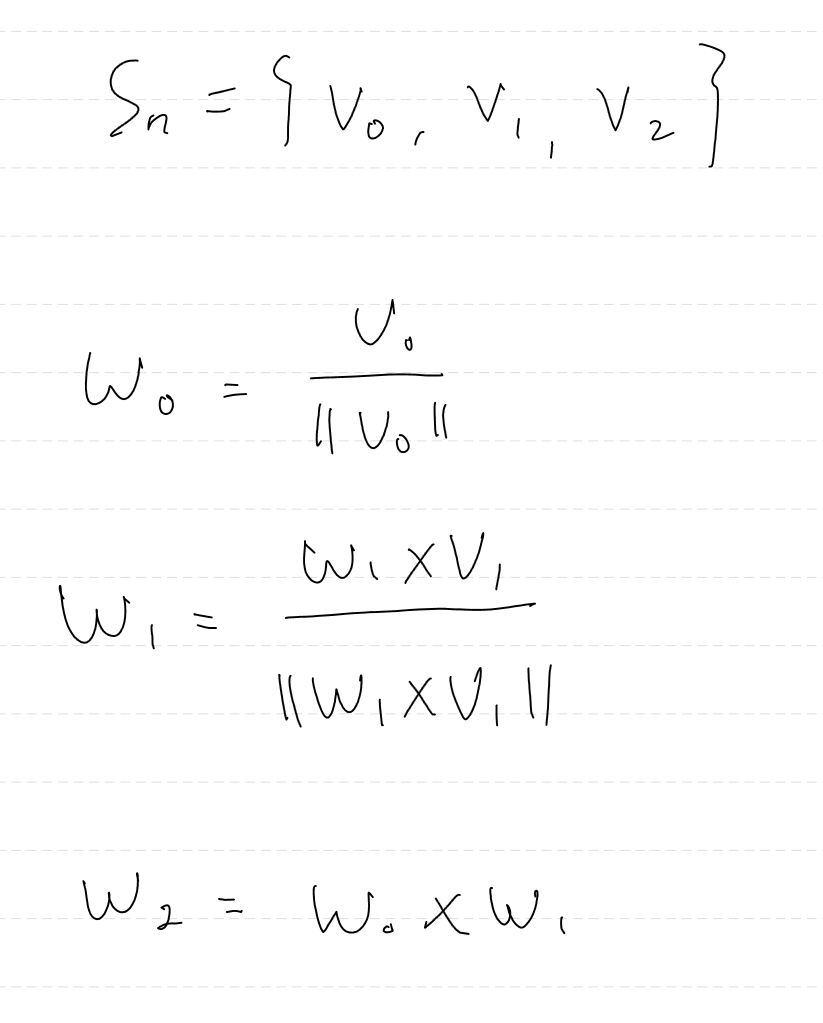
w2 구할 때 눈여겨 봐야할 점은
w0와 w1가 이미 정규화 벡터이기에, w2의 크기는 1이라는 것이다.
직교화 할 때는 어떤 벡터를 기준으로 직교화를 수행할 것인지 생각해야한다.
w0을 제외하고 w1, w2는 기존 벡터인 v1, v2와 사뭇 다른 벡터가 될 수 있기 때문이다.
이 책의 후반부에서는 3개의 직교 벡터 {v0, v1, v2} 로 카메라의 방향을 나타내며, v2는 카메가라 바라보는 방향을 나타낸다.
이 벡터들을 직교화 할 때는 v2를 w0으로 두어, v2를 기준으로 직교화를 수행해야 한다.
점 Point
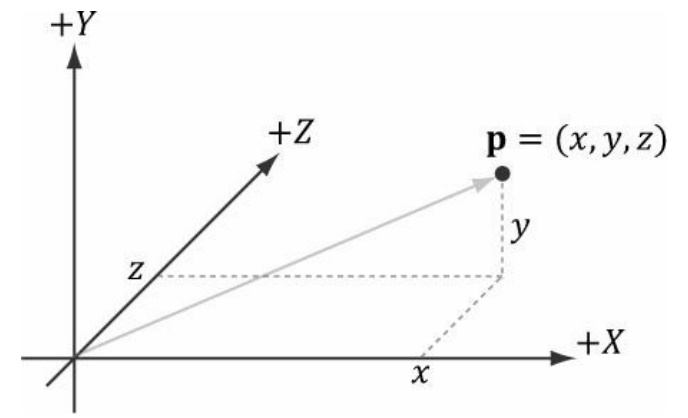
지금까지 벡터에 대해 논의해왔다. 우리는 3D 프로그램에서 기하학의 위치 등을 표현하기 위해서 점이라는 개념이 필요하다. 좌표계와 벡터를 사용하여 3D 위치를 나타낼 수 있으며, 이를 위치 벡터라고 한다.
이 경우, 우리가 관심을 가지는 특성은 벡터의 방향, 크기보다는 벡터 끝점의 위치이다.
위치 벡터가 점을 식별하는 데 충분하므로, 위치 벡터와 점은 혼용하여 사용할 수 있다.
그러므로, 우리는 좌표계에 점을 표현하기 위해서 벡터를 사용할 수 있고, 벡터 대수의 틀에서 점과 벡터 사이의 연산을 정의할 수 있다.
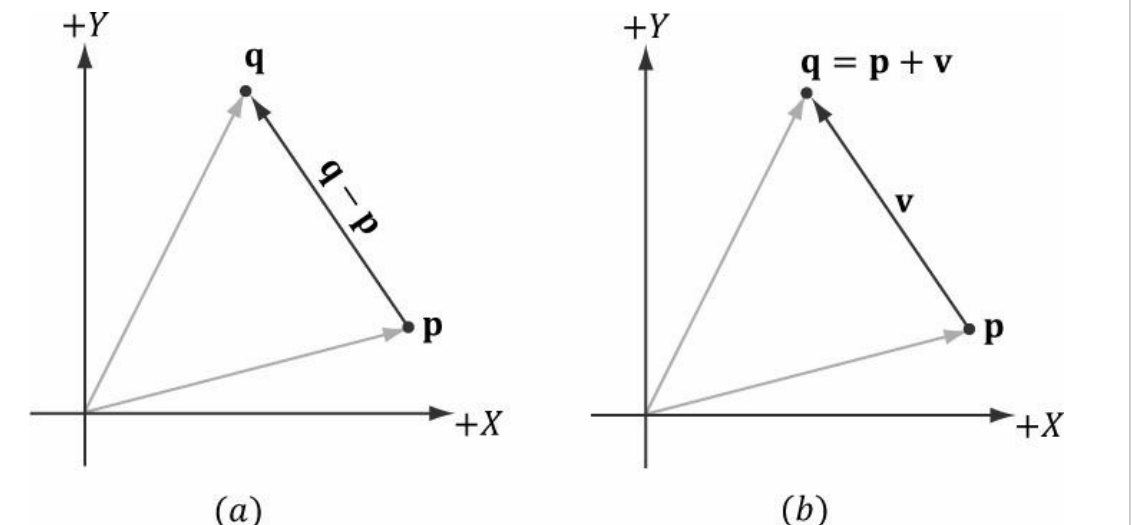
두 점 q, p 사이의 뺄셈은 p에서 q로 향하는 벡터를 정의하고
점 p에 벡터 v를 더하면 새로운 점 q를 얻어낼 수 있다.
점들 사이의 합은 특수하게 정의해야 하는데, 이를 아핀 결합이라고 한다.
DirectXMath.h
교재에서는 XNAMath 를 사용하지만, 현재 버전에서는 지원이 중단되어
현재 버전에서 사용되는 DirectXMath를 이용하여 예제를 작성한다.
DirectXMath는 SIMD(병렬 컴퓨팅의 한 종류로, 하나의 명령어로 여러 개의 값을 동시에 계산하는 방식) 최적화를 활용하여 높은 성능을 보이는 수학 라이브러리이다.
1. 벡터타입
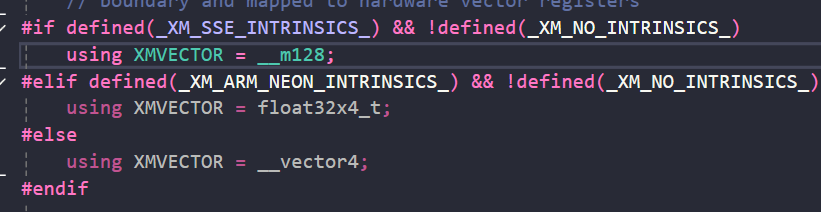
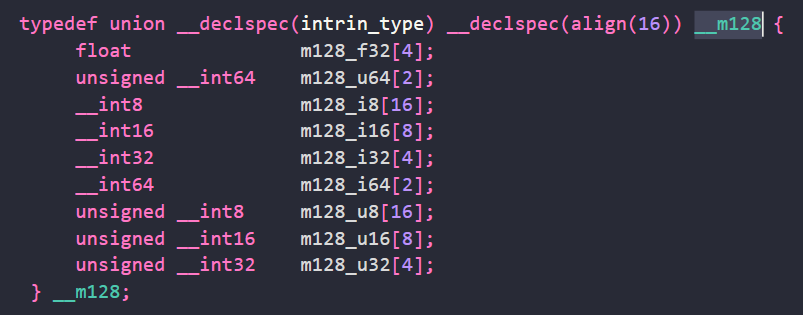
XMVECTOR는 4D 벡터 타입이다.
float 배열 4개로 이루어진 128비트 (16바이트) 구조체이다.
이런식으로 __m128 데이터 타입을 사용하는 이유는 SIMD 명령어를 사용하기 위함이다.
128비트 짜리 특수한 구조체를 이용하여 한 번의 SIMD 명령어로 32비트 flaot 4개를 처리할 수 있다.
계산을 할 때, SIMD의 이점을 활용하려면 벡터가 해당 타입이어야 한다.
2D 및 3D 벡터에서도 SIMD의 이점을 활용하기 위해 이 타입을 사용해야하며, 사용하지 않는 성분은 0으로 설정하고 무시한다.
XMVECTOR은 16바이트 정렬이 필요하다. 이 뜻은 메모리에서 데이터가 시작하는 주소가 16으로 나누어떨어지는 위치에 배치된다는 것을 말한다.
CPU는 16바이트로 정렬된 데이터를 더 효율적으로 읽고 쓸 수 있기 때문에, 데이터가 16바이트 경계에 정렬되지 않으면, CPU는 추가 작업을 수행해야 하고, 성능이 떨어질 수 있다. 또, SIMD 명령어는 데이터가 16바이트 단위로 정렬되어 있어야 올바르게 작동한다.
로컬 변수와 전역 변수의 경우, C++ 컴파일러가 자동으로 16바이트로 정렬해 주기 때문에 XMVECTOR를 사용할 때 신경 쓸 필요가 없지만, 동적 할당 또는 클래스 멤버로 XMVECTOR를 사용할 경우, 16바이트 정렬이 보장되지 않기 때문에 수동으로 정렬을 보장해줘야 한다.
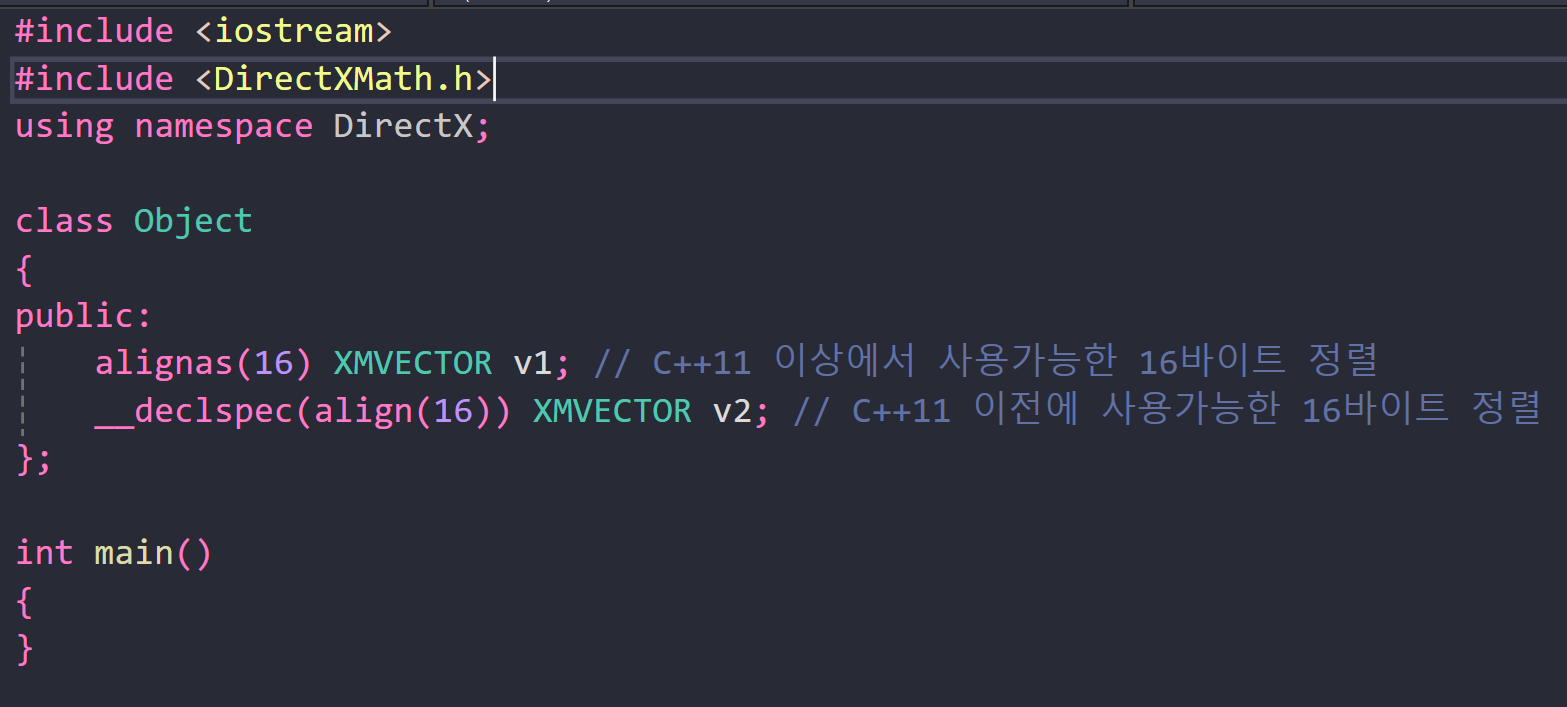
클래스의 데이터 멤버의 경우, 대신 XMFLOAT2, XMFLOAT3, XMFLOAT4 를 사용하는 것이 권장된다.
그 이유는 클래스의 멤버 변수를 사용할 때, 모든 멤버가 동일하게 정렬되거나 16바이트로 정렬되지 않을 수 있기 때문이다. 이러한 경우, 정렬되지 않은 XMVECTOR를 사용하는 것은 성능 저하를 발생시킬 수 있다.
그래서 클래스의 멤버, 동적 할당시에는 정렬 요구사항이 상대적으로 덜 엄격한 XMFLOAT2, XMFLOAT3, XMFLOAT4 같은 구조체를 사용하는 것이 좋다.
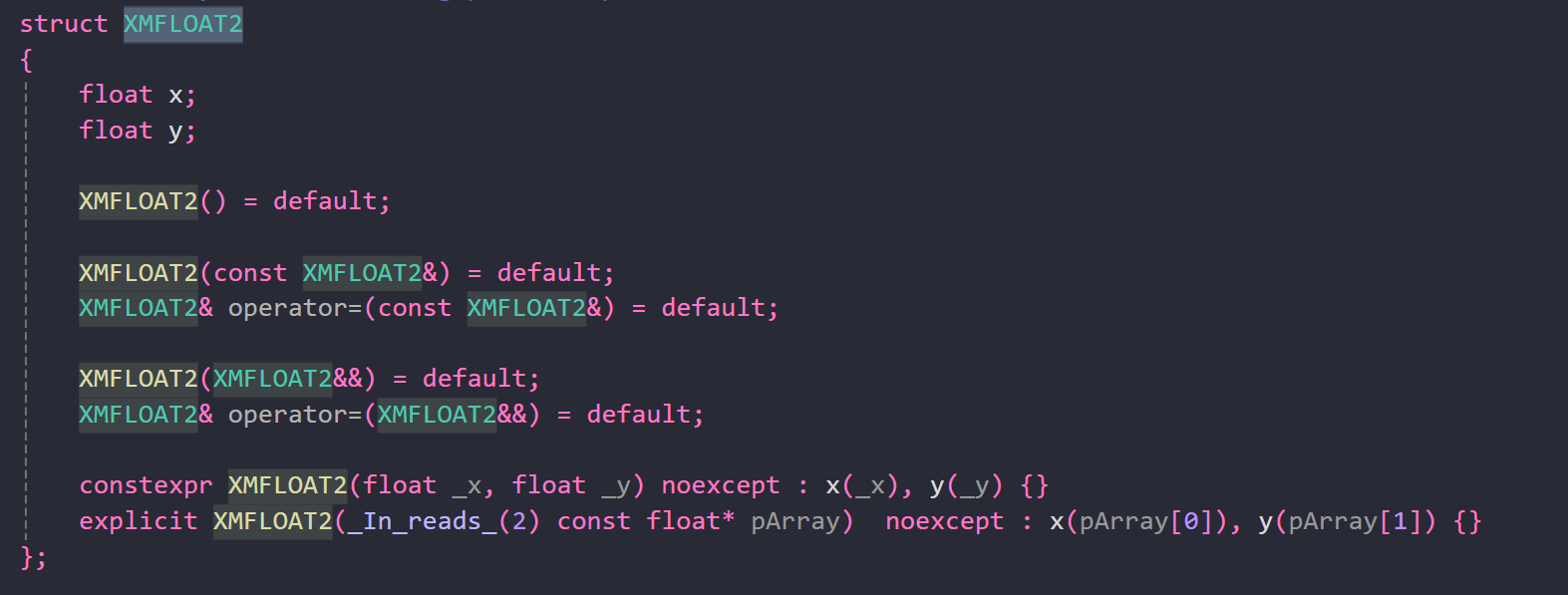
해당 데이터 타입들은 구조체에 불과하다.
즉, 일반적인 데이터 저장과 직관적인 사용에 적합하며,
실제 연산할 때는 XMVECTOR 로 변환한 후 연산하는 것이 일반적인 패턴이다.
이렇게 하면 메모리 정렬 문제를 회피하면서도, 연산에서의 성능을 극대화할 수 있다.
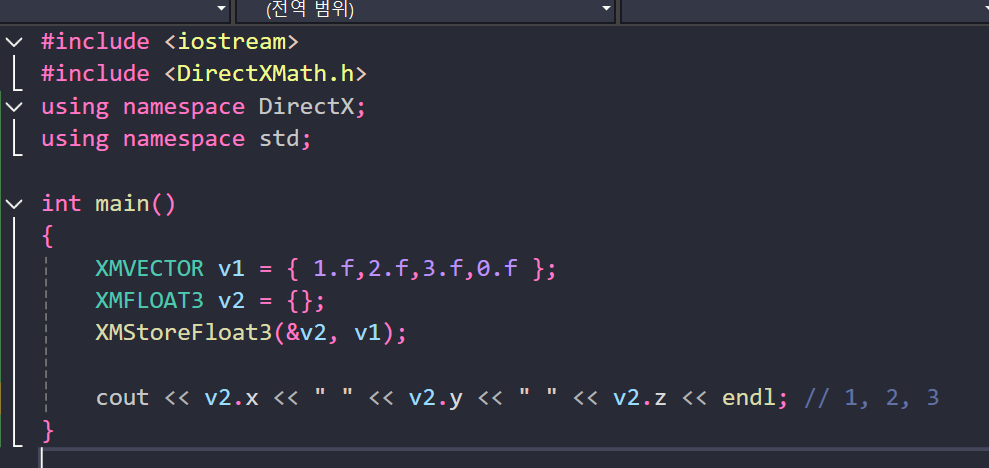
MXVECTOR를 XMFLOAT3 로 변환하는 예제
DX3D의 작명법은 직관적으로 이해할 수 있다.
"저장한다 FLOAT3를"
MXVECTOR의 값을 FLOAT3에 저장한다는 의미이다.
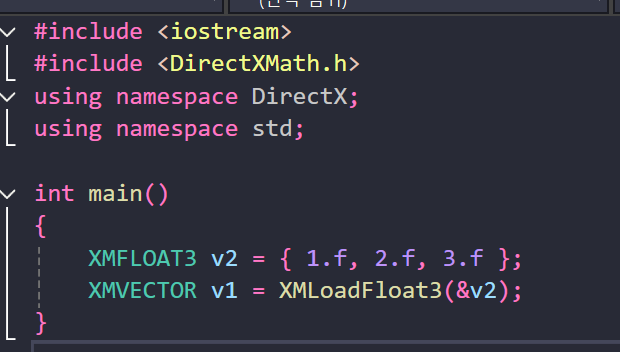
XMFLOAT3를 MXVECTOR로 변환하는 예제
Load를 이용해서 XMVECTOR에 XMFLOAT의 데이터를 불러올 수 있다.
"불러온다. FLOAT3에서"
FLOAT3값을 불러와서 리턴한다.
요약
1. 로컬 또는 전역 변수에는 XMVECTOR를 사용한다.
2. 클래스 멤버에는 XMFLOAT2, XMFLOAT3, XMFLOAT4 를 사용한다.
3. 계산을 하기 전에 로딩 함수를 사용하여 XMFLOAT에서 XMVECTOR로 변환한다. 이러면 SIMD 최적화의 이점을 사용할 수 있다.
4. XMVECTOR 인스턴스로 계산을 수행한다.
5. 저장 함수를 사용하여 XMVECTOR에서 XMFLOAT로 변환한다.

이런 Store함수도 지원한다고 하는데 XMStoreColor는 지원이 끊긴것으로 사료됨.
2. Getter, Setter
XMVECTOR의 하나의 성부만 가져오거나 설정하고 싶을 때, 용이하게 사용할 수 있다.
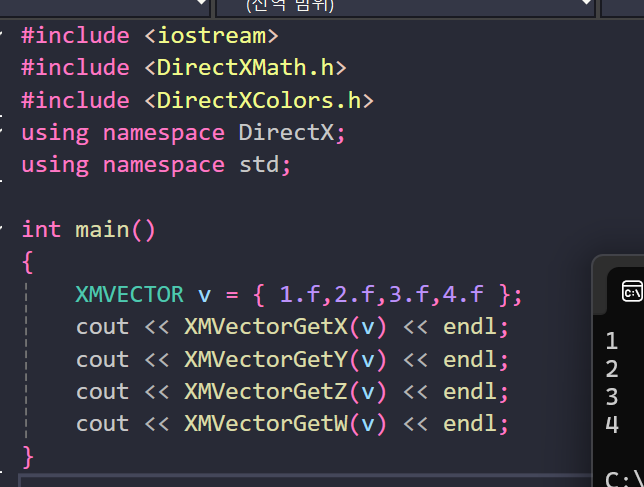
Getter
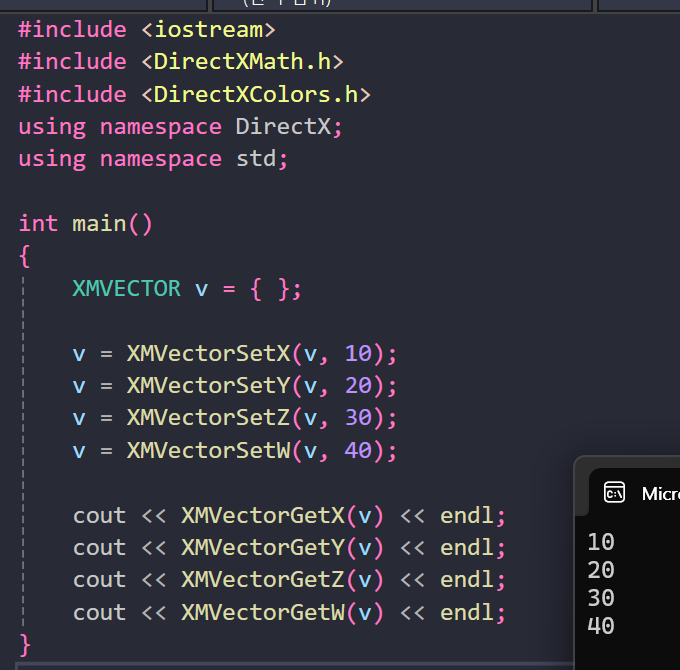
Setter
3. 파라미터 전달
SIMD를 최대한 활용하려면 XMVECTOR 타입의 파라미터를 함수에 전달할 떄 몇가지 규칙을 따라야 한다.
이 규칙은 플랫폼에 따라 다르며, 32비트, 64비트 플랫폼간에 차이가 있다.
플랫폼에 독립적인 코드를 작성하기 위해, 우리는 XMVECTOR 파라미터를 전달할 떄는 CXMVECOTR와 FXMVECTOR 타입을 사용하며, 이는 플랫폼에 따라 적절한 타입으로 정의된다.

위 두 타입의 차이는 참조냐 복사냐 이다.
4. 상수 벡터
상수 XMVECTOR 인스턴스는 XMVECTORF32 타입이다.

XMVECTORF32는 정렬 16바이트 구조체이고, 사싱상 XMVECTOR와 동일하다고 여길 수 있다.
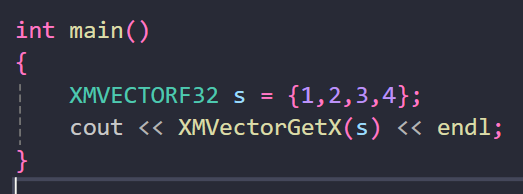
위와같이 XMVECTOR와 동일하게 사용할 수 있으나, const 이기 때문에 값이 바뀌지는 않는다.
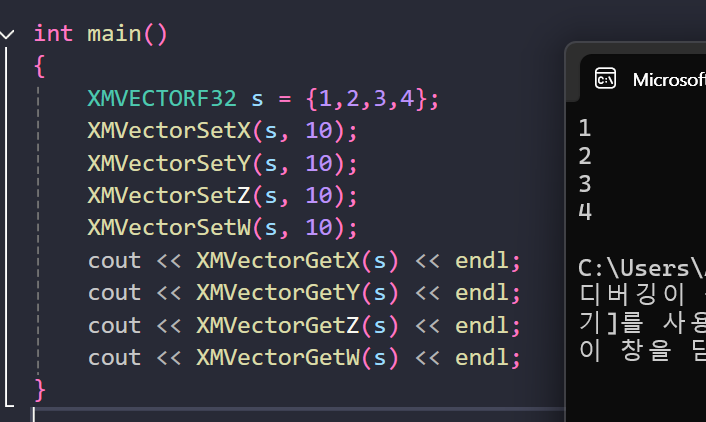
본질적으로, 초기화 구문을 사용할 때는 XMVECTORF32를 사용한다.
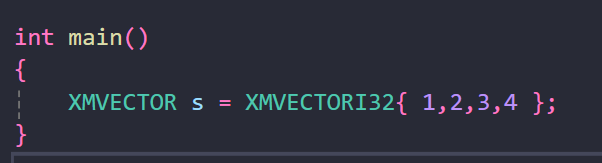
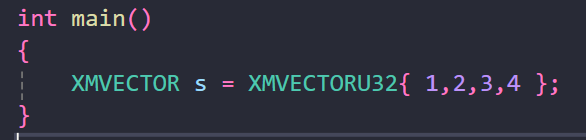
정수 형식으로 초기화 할 때는 위와 같은 구문을 사용하는 것이 일반적이다.
5. 연산자 오버로딩
XMVECTOR는 벡터 덧셈, 뺼셈, 스칼라 곱셈 등을 수행하기 위한 여러 연산자 오버로딩을 지원한다.
XM_NO_OPERATOR_OVERLOADS를 정의하여 연산자 오버로딩을 비활성화할 수 있다.
연산자 오버로딩은 성능 저하를 일으킬 수 있기 떄문에, 일부 애플리케이션에서는 연산자 오버로딩을 비활성화시키곤 한다. 복잡한 수식을 구성할 때 함수 버전이 더 빠를 수 있다.

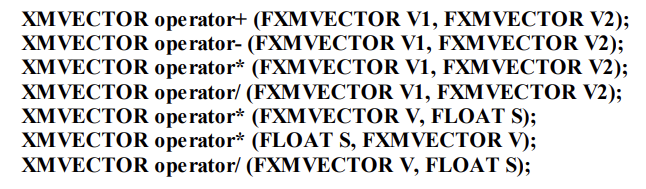

*, / 은 벡터들의 요소들 끼리는 곱과 나눗셈이다.
5. 기타
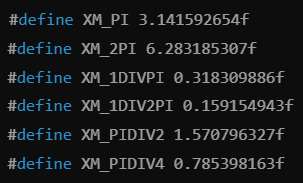
파이 근사화 매크로

라디안 도 변환 인라인 함수

최대 최소
6. 벡터 함수들

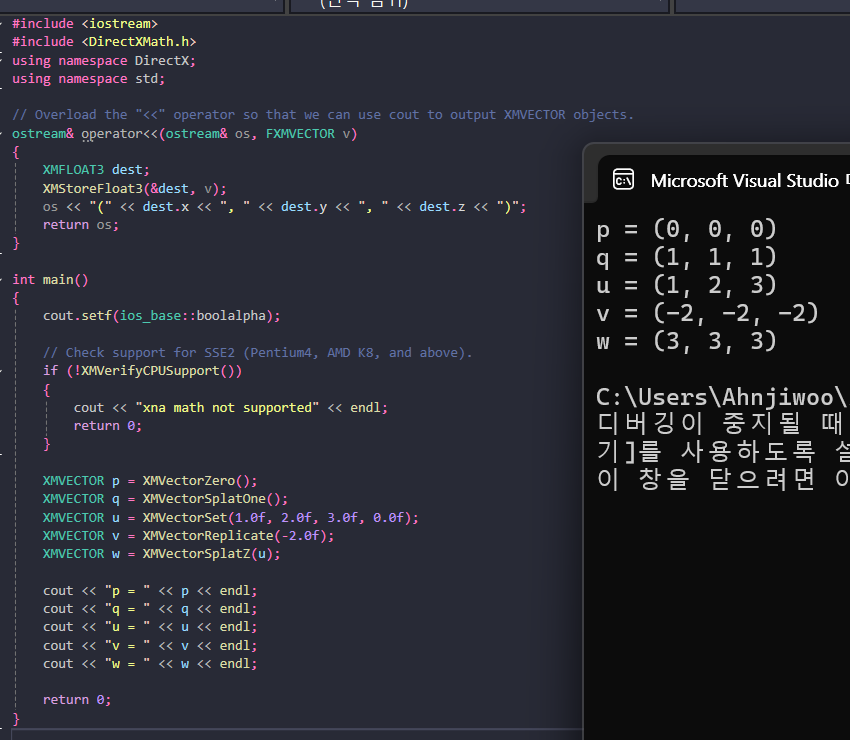

XMVector3Orthogonal << 이 함수는 입력된 벡터에 대해서 임의의 직교벡터를 반환한다.
XMVector3AngleBetweenVectors << 이 함수는 벡터를 반환하는데 벡터의 요소는 모두 동일하고, 라디안 값을 나타낸다.
만약 두 벡터가 정규화되어 있다면 XMVector3AngleBetweenNormals 를 사용할 수 있다. (연산량이 더 적다.)
DirectXMath는 더 빠르지만 덜 정확한 몇 가지 근사치 함수도 포함하고 있다.
그러므로 정확도를 약간 포기하고 속도를 우선시하기 위해 근사 함수를 사용할 수도 있다.

7. 부동소수점 오류
부동소수점은 불안전성 때문에 주의해야 한다.
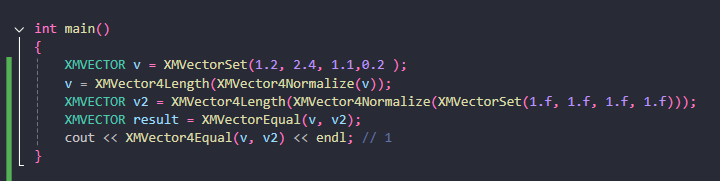
같다고 기대하는 두 부동소수점 수는 오차가 존재할 수 있다.
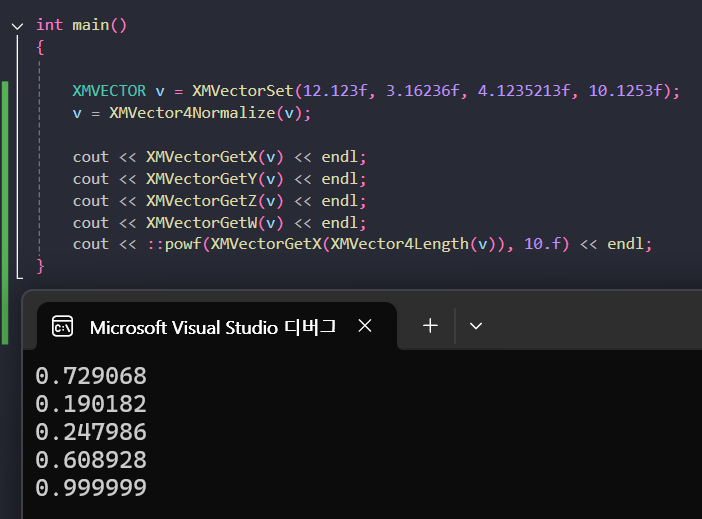
정규화된 벡터의 길이는 1이다.
그러므로 10승을 하든 100승을 하든 1이어야 한다.
그러나 float의 구조상 오차가 발생하는 것은 막을 수 없다.
부동소수점의 불완전성을 보완하기 위해서 두 부동소수점을 비교할 때는 두 숫자가 대략적으로 같은지 판단해야한다.
이를 위해 매우 작은 값을 가진 Epsilon 상수를 정의하고, 두 값 사이의 차이가 Epsilon 보다 작으면 대략적으로 동일하다고 여길 수 있다.
Epsilon은 불완전성에 대한 허용 오차 (Error 혹은 Tolerence) 를 제공한다.
즉, 두 XMVECTOR을 (근사치로) 비교하기 위해서는 XMVector4NearEqual을 사용하면 된다.
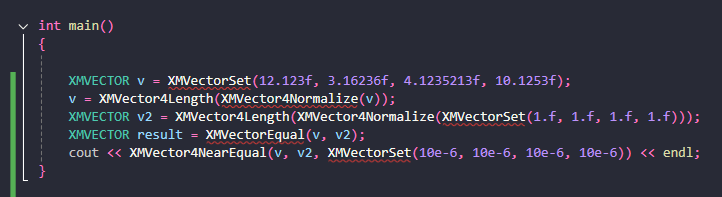
첫 번째 두 번째 매개변수로 비교할 벡터를
세 번째 매개변수로 허용오차를 넣으면 된다.
'컴퓨터 그래픽스 > DirectX 11' 카테고리의 다른 글
| [DX11 물방울책 요약 정리] 챕터5: 렌더링 파이프라인 (0) | 2024.09.15 |
|---|---|
| [DX11 물방울책 요약 정리] 챕터4: Direct3D 초기화 (0) | 2024.09.08 |
| [DX11 물방울책 요약 정리] 챕터3: Transformations (1) | 2024.09.07 |
| [DX11 물방울책 요약 정리] 챕터2: 행렬 대수 (0) | 2024.09.07 |
| [DX11 물방울책 요약 정리] 머리말 (3) | 2024.09.05 |



