이 장의 주요 주제는 렌더링 파이프라인이다.
가상 카메라가 배치되고 방향이 설명된 3d 장면의 기하학적 설명을 바탕으로,
렌더링 파이프라인은 카메라가 보는 것을 기반으로 2D 이미지를 생성하는 일련의 과정 전체를 의미한다.

말이 어려울 수도 있는데..
월드에 3D 기하학들이 정해져 있고, 카메라는 특정 공간을 미추고 있다.
3D 기하학 정보들을 적절하게 해석하여 뷰포트에 2D 형태로 이미지를 생성하는 과정을 렌더링 파이프라인이라고 한다.
외 그림에서 왼쪽이미지는 카메라가 위치하고 조준된 3D 월드의 객체들의 측면 뷰를 보여준다.
가운데 이미지는 같은 장면을 위에서 내려다본 모습이다.
카메라의 시야 (피라미드 모양, 혹은 절두체라고 부름) 은 볼 수 있는 공간의 부피 (가시부피)를 나타내며, 해당 공간 외부에 있는 객체는 보이지 않는다.
최종적인 목표는 카메라가 본 것을 바탕으로 2D 이미지를 생성하는 것이다.
이 장은 주로 이론적이며, 다음 장에서는 Driect3D를 사용하여 이 이론을 실제로 적용하는 방법을 배운다.
렌더링 파이프라인에 대한 설명을 시작하기 전에 두 가지 짧은 주제를 다룬다.
첫 번째로, 3D 일루전 (2D 모니터 화면을 통해 3D 세계를 보고 있다는 환상) 에 대해 논의하고
두 번째로, 색상이 수학적으로, 코드로 어떻게 표현되고 다뤄지는지 설명한다.
목표
1. 2D 이미지에서 실제적인 부피감과 공간적 깊이를 전달하는 몇 가지 주요 신호를 발견한다.
2. Direct3D에서 3D 객체를 어떻게 표현하는지 알아본다.
3. 가상 카메라를 어떻게 모델링하는지 배운다.
4. 렌더링 파이프라인, 즉 3D 장면의 기하학적 설명을 받아 2D 이미지를 생성하는 과정을 이해한다.
3D Illusion
3D 컴퓨터 그래픽스를 시작하기 전에 한 가지 간단한 질문이 남아있다.
어떻게 평평한 2D 모니터 화면에 깊이와 부피가 있는 3D 세계를 표현할 수 있을까?
다행히도 이 문제는 오래전부터 연구되어 았으며, 예술가들은 수세기 동안 2D 캔버스에 3D 장면을 그려왔다.
이 절에서는 2D 평면에 그려진 이미지가 3D처럼 보이게 만드는 몇 가지 주요 기법을 설명한다.
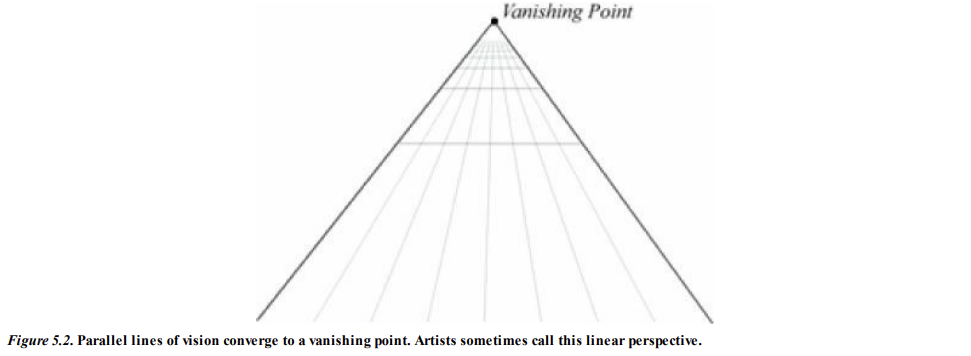
철로는 길이 내내 서로 평행을 유지하지만, 철로에 서서 그 길을 보면
두 철로는 멀어질수록 점점 가까워지다가, 결국 무한한 거리에서 한 점으로 수렴하는 것을 관찰할 수 있다.
그러한 점을 소실점이라고 한다.
예술가들은 이를 선 원근법 (Linear Perspective) 라고 한다.
이는 가까운 물체는 멀리 있는 물체보다 크게 보인다는 것을 시사한다.

기둥들은 실제로 모두 같은 크기지만, 관찰자로부터 깊이가 커질수록 점점 작아 보인다.
또한, 기둥들이 수평선의 소실점으로 수렴하는 것을 주목하라.

우리는 모두 물체의 겹침을 경험한다.
이는 불투명한 물체가 그 뒤에 있는 물체의 일부 또는 전체를 가린다는 사실이다.
자세한 것은 깊이 버퍼에 대해서 논의했으므로 넘어가도록 한다.

왼쪽의 구는 상당히 평평해 보인다. 구인지 텍스처가 입혀진 2D 원일지도 모른다.
따라서 조명과 음영(Lighting, Shading) 은 3D 객체의 고체 형태와 부피를 묘사하는 데 매우 중요한 역할을 한다.

마지막으로 우주선과 그 그림자를 보여준다.
그림자는 두 가지 중요한 역할을 하는데,
첫 번째로, 그림자는 장면 내의 광원 위치를 알려주고
두 번쨰로, 그림자는 객체가 지면에서 얼마나 떨어져 있는지를 대략적으로 알 수 있게 해준다.
지금까지 논의한 관찰들은 일상적인 경험으로부터 직관적으로 명백한다.
원근, 깊이감, 광원, 음영, 그림자 등은 2D 화면에 3D 세계를 표현함에 있어 설득력을 더하는 도구가 된다.
모델 표현
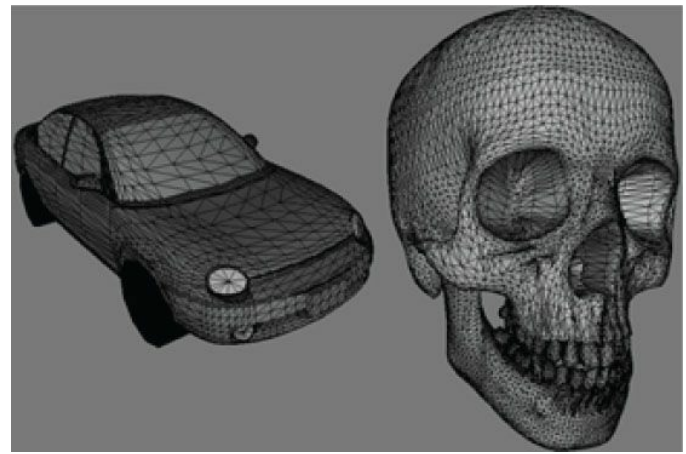
Solid 3D 객체는 삼각형 메시 근사로 표현되며, 따라서 삼각형은 우리가 모델링하는 객체의 기본 구성 요소이다.
즉, 우리는 실세계의 3D 객체를 삼각형을 이용하여 근사화 할 수 있다.
객체를 근사화하는 데 많은 삼각형을 사용할 수록 더 정밀한 세부 사항을 모델링할 수 있다.
물론, 더 많은 삼각형을 사용할수록 더 많은 계산 능력이 필요하므로, 애플리케이션의 대상 사용자가 사용하는 하드웨어 성능에 따라 균형을 맞춰야 한다.
삼각형 외에도, 때때로 선이나 점을 그리는 것이 유용할 수 있다.
예를 들어, 곡선은 픽셀 두께의 짧은 선분들로 이루어진 순서를 통해 그래픽적으로 그릴 수 있다.
위 그림에서 보듯.. 삼각형으로 3D 객체를 수동으로 정의하는 것은 불가능할 정도로 번거롭다.
그래서 단순한 모델을 제외하고는, 3D 모델링 애플리케이션을 사용하여 3D 객체를 생성하고 조작한다.
모델링 애플리케이션은 복잡하고 사실적인 메시를 손쉽게 구축할 수 있게 한다.
게임 개발에 사용되는 모델러는 3D Studio Max, LightWave 3D, Maya, Sofimage, Blender 등.. 이 있다.
그럼에도 불구하고, 이 책의 첫 번째 부분에서는 3D 모델을 수작업으로 생성하거나 수학적 공식으로 생성할 것이다.
이 책의 세 번째 부분에서는 3D 모델링 프로그램에서 내보낸 3D 모델을 로드하고 표시하는 방법을 보여준다.
기본 컴퓨터 색상
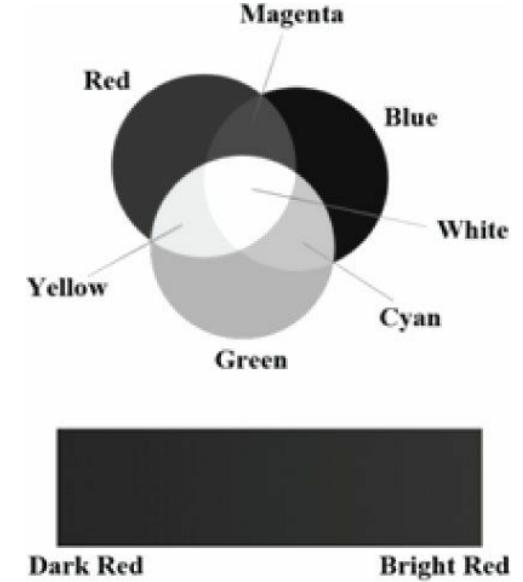
컴퓨터 모니터는 각 픽셀을 통해 빨간색, 녹색, 파란색 빛의 합성을 묘사한다.
이 빛의 합성은 눈에 들어와 망막의 특정 부위에 도달하면, 원뿔 세포 수용기가 자극되어 신경 자극이 시신경을 따라 뇌로 전달된다.
뇌는 이 신호를 해석하여 색상을 생성한다.
빛의 혼합물이 변하면 세포가 다르게 자극되어 결국 다른 색상이 만들어진다.
우리는 각 색상 구성 요소의 강도를 다르게 설정하고 이를 혼합함으로써, 현실적인 이미지를 표시하는 데 필요한 모든 색상을 표현할 수 있다.
모니터는 방출할 수 있는 빨간색, 녹색, 파란색 빛의 최대 강도를 가지고 있다.
이를 직관적으로 설명하기 위해, [0, 1]로 정규화된 범위를 사용하는 것이 유용하다.
물론, 1에 가까울 수록 빛의 세기가 강함을 의미한다.
r, g, b는 각각 [0, 1] 범위 내에서 정의되며, 각각의 색상 구성 요소들을 합성하여 새로운 색상을 만들 수 있다.
색상 연산
일부 벡터 연산은 색상 벡터에도 적용된다.
예를 들어, 색상 벡터를 더하여 새로운 색상을 얻을 수 있다.
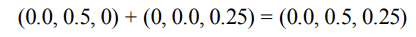
물론 뺄셈도, 스칼라 곱셈도 의미를 가진다.
단, 색상 벡터의 Dot Product나 Cross Product는 의미를 가지지 않는다.
그러나 색상 벡터는 모듈레이션 (또는 요소 곱셈) 이라는 특별한 연산을 가진다.
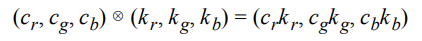
이는 요소 별로 곱하는 연산이다.
이 연산은 주로 조명 방정식에서 사용된다
예를 들어, (r, g, b) 색상의 빛이 표면에 닿았다고 가정하자.
그리고 이 표면은 50%의 빨간색 빛, 75%의 녹색 빛, 25%의 파란색 빛을 반사한다고 해보자.
그렇다면 반사된 빛의 색상은 다음과 같이 계산된다.
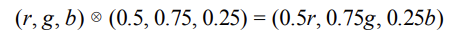
이는 표면의 색상을 고려하여 광원의 일부는 반사하고, 나머지는 흡수한다는 것을 보여준다.
색상 연산을 할 떄, 색상 구성 요소가 [0, 1] 범위를 벗어날 수 있다. 그러나 [0, 1] 의 범위는 지켜줘야 하므로 [0,1] 범위로 직접 clamp 해줘야 한다.
(정확히 말하면, 1 범위를 넘어가는 값들은 모두 1과 결과가 동일하다. 0 범위를 넘어가는 값들은 모두 0과 결과가 동일하다.)
128 bit Color
색상 데이터는 알파 요소를 포함하는 것이 일반적이다.
알파 요소는 색상의 불투명도를 나타내는 데 사용되며, 블렌딩에서 유용하다.
알파 값이 1일 경우 불투명, 알파 값이 0일 경우 투명하다는 것을 의미한다.
알파 구성 요소를 포함하면 색상을 [0, 1] 범위의 4D 벡터로 표현할 수 있다. (r, g, b, a)
수학적으로 색상은 단순히 4D 백터이므로, XMVECTOR 타입을 사용하여 색상을 표현할 수 있으며, SIMD 연산의 이점을 얻을 수 있다.
XMColorModulate 라는 모듈레이터를 지원하는 함수도 존재한다.
32 bit Color
32비트로 색상을 표현하는 것은 매우 고전적인 방법이다.
1바이트 단위로 R, G, B, A를 각각 할당하며, 각 색상 구성 요소는 256가지의 다른 색조를 표현할 수 있다.
32 bit Color의 경우 [0, 255] 범위를 값으로 가질 수 있다.
과거에 _XMCOLOR라 하여, 32bit 색상 구조체를 제공하였으나, 최근 라이브러리에서는 32 bit Color를 더 이상 지원하지 않는다.
그러므로 더 이상의 설명은 생략하도록 한다.
일반적으로, 많은 색상 연산이 발생하는 곳(픽셀 셰이더 등..) 에서는 128비트 색상 값을 사용한다.
128비트 색상은 정확성이 높기 때문에 산술이 오류 누적을 최소화한다.
결국 최종 픽셀 생삭은 백 버퍼에 32비트 색상 값으로 저장된다. 그 이유는 현재의 물리적 디스플레이 장치는 32비트 색상을 지원하기 때문이다.
렌더링 파이프라인 개요
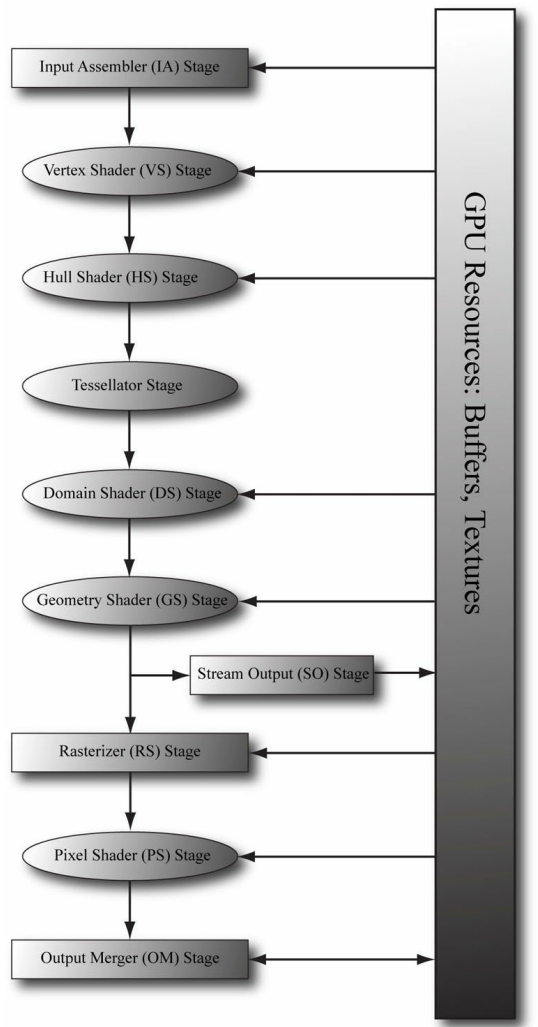
렌더링 파이프라인은 가상 카메라가 보는 것을 기반으로 2D 이미지를 생성하기 위해 필요한 모든 단계의 순서를 말한다.
렌더링 파이프라인의 단계를 보여주는 위 그림은 GPU 메모리 리소스의 흐름도 설명해준다.
메모리 리소스에서 파이프라인으로의 화살표는 그 단계의 입력으로 리소스를 사용할 수 있음을 의미한다.
예를 들어 Pixel Shader Stage (PS)는 작업을 수행하기 위해 메모리에 저장된 텍스처 리소스의 데이터를 읽어서 사용할 수 있다.
파이프라인에서 메모리로 가는 화살표는 그 단계에 GPU 리소스에 데이터를 쓴다는 것을 의미한다.
예를 들어, Output Merge Stage(OM) 단계는 백 버퍼와 깊이/스텐실 버퍼와 같은 텍스처에 데이터를 쓴다.
OM 단계의 화살표는 특이하게 양방향 화살표이다. 대부분의 단계는 GPU 리소스를 읽기만 한다.
대신, 그들의 출력은 파이프라인의 다음 단계에 입력으로 전달될 뿐이다.
예를 들어, Vertex Shader(VS) 단계는 Input Assembler 단계에서 데이터를 입력받아 자체 작업을 수행하고 그 결과를 Geometry Shader 단계에 출력한다.
다음 섹션에서는 렌더링 파이프라인의 각 단계에 대한 개요를 제공한다.
Input Assembler Stage (IA)
Input Assember State 이하 IA 단계는 메모리에서 버텍스와 인덱스라는 기하학 데이터를 읽어와서 이를 사용하여 기하학적 프리미티브 (삼각형, 선 등..)을 구성한다.
1. Vertices
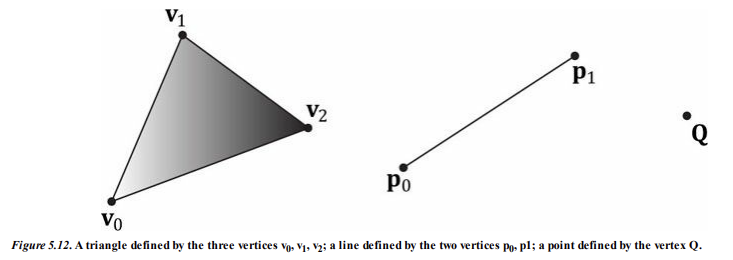
수학적으로 삼각형의 버텍스는 두 변이 만나는 지점이고, 선의 버텍스는 끝점이며, 단일 점의 경우 그 점 자체가 버텍스이다.
위 그림과 설명을 미루러보아, 버텍스는 기하학 도형을 정의하는데 있어 필요한 점에 불과한 것처럼 보인다.
하지만 Direct3D에서 Vertex는 더 많은 의미를 가지고 있다.
본질적으로 Drirect3D의 버텍스는 공간 상에서 위치에 더하여 추가적인 정보를 포함할 수 있다.
이러한 정보들은 정교한 렌더링 효과를 구현하는데 도움을 준다.
예를 들어, 조명을 구현하기 위해 버텍스에 노멀 벡터를 추가할 수 있고, 텍스처링을 구현하기 위해 Vertex에 UV 좌표를 추가할 수 있다.
Driect3D는 우리가 직접 버텍스 포맷을 정의할 수 있는 유연성을 제공하며, 이를 수행하는 코드는 다음 장에서 살펴볼 것이다.
이 책에서는 우리가 수행하는 렌더링 효과에 따라 여러 가지 다른 Vertex 포맷을 정의할 것이다.
2. Primitive Topology (원시 위상)
Vertex는 Vertex Buffer라고 불리는 특별한 Driect3D의 자료 구조에 정의되어 렌더링 파이프라인으로 바인딩된다. Vertex BUffer는 연속된 메모리에 Vertex 목록을 저장한다.
그러나 VertexBuffer 그 자체로는 Vertex가 기하학적인 도형을 만들기위해 어떻게 조합되어야 하는지는 설명하지 않는다.
버텍스는 단순히 말하자면 위치 정보만 가지고 있는 점이기 때문에.. 버텍스를 선으로 해석할지, 삼각형으로 해석할지는 Primitive Topology 를 지정해서 Direct3D가 어떤 식으로 버텍스를 해석해야하는지 알려줘야만 한다.

D3D11_PRIMITIVE_TOPOLOGY enum
한 번 설정한 프리미티브 토폴로지는 변경될 떄까지 계속 유지된다.
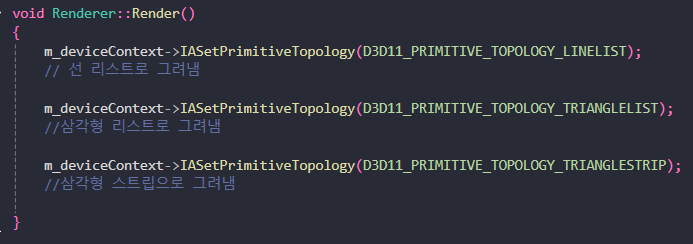
이 책에서는 triangle list를 기본적으로 사용한다.
1. Point List
포인트 리스트는 D3D11_PRIMITIVE_TOPOLOGY_POINTLIST로 지정된다.
포인트 리스트에서는 Draw Call이 모든 베텍스가 개별적인 점으로 그려진다.
2. Line Strip
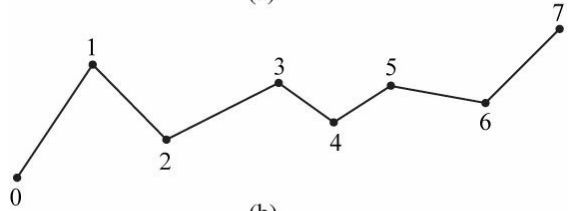
라인 스트립은 D3D11_PRIMITIVE_TOPOLOGY_LINESTRIP로 지정한다.
라인 스트랩은 버텍스들이 연결되어 선을 형성하며, n+1개의 버텍스는 n개의 선을 만든다.
점과 점이 선을 만들고 이전 점을 이용해서 선을 이어나간다... 라고 이해하면 편하다.
3. Line List
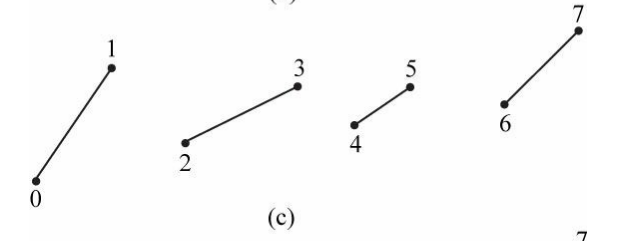
라인 리스트는 D3D11_PRIMITIVE_TOPOLOGY_LINELIST로 지정된다.
라인 리스트는 두 버텍스마다 개별적인 선을 형성한다.
즉, 2n개의 버텍스는 n개의 선을 만든다.
라인 리스트와 스트립의 차이점은
리스트는 선들 하나하나를 잇는것
스트랩은 이전 버텍스들을 이용해서 렌더링을 이어나가는 것 이라고 이해할 수 있다.
복잡하지만, 연결성을 잘 이해한다면 스트랩은 더 적은 버텍스로 프리미티브 도형을 정의할 수 있을 것이다.
4. Triangle Strip
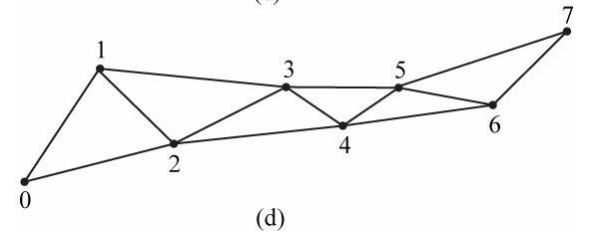
삼각형 스트립은 D3D11_PRIMITIVE_TOPOLOGY_TRIANGLESTRIP 로 지정된다.
삼각형 간에 버텍스를 공유하며 n개의 버텍스는 n - 2개의 삼각형을 만든다.
삼각형 스트립에서는 짝수번째 삼각형의 와인딩 순서 (삼각형을 그리는 순서)가 홀수번째 삼각형의 와인딩 순서와 반대이다.
이것은 백 페이스 컬링을 구현함에 있어 치명적이다.
백 페이스 컬링은 보통 시계방향으로 정의된 삼각형을 전면으로 인식하여 렌더링하고
반시계방향으로 정의된 삼각형을 후면으로 인식하여 렌더링하지 않는다.
이 문제를 해결하기 위해 GPU는 내부적으로 짝수 삼각형의 첫 두 버텍스 순서를 교환하여 홀수 삼각형처럼 일관된 순서로 정의한다
5. Triangle List
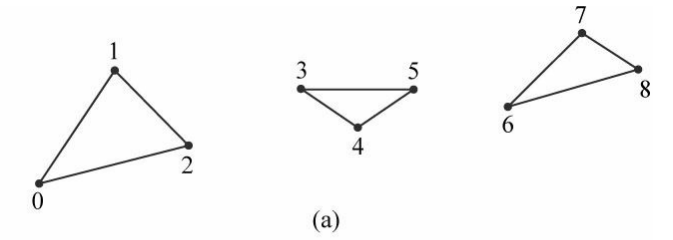
삼각형 리스트 D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST로 지정된다.
삼각형 리스트에서는 드로우 호출의 세 버텍스마다 개별 삼각형을 형성하며, 3n개의 버텍스는 n개의 삼각형을 만든다.
삼각형 리스트와 스트립의 차이점은 앞서 말한 리스트와 스트립의 차이점과 동일하다.
6. 인접한 도형 Primitives with Adjacency
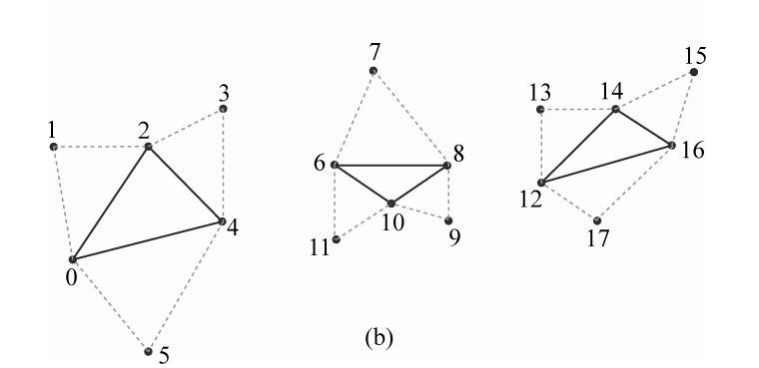
인접성을 표현하는 것은 중요하며, 그저 비슷한 위치에 도형을 정의한 것으로는 부족하다.
삼각형 리스트에서 각 삼각형은 자신과 인접한 삼각형을 설명하기 위해 삼각형 당 3개의 버텍스를 추가로 사용한다.
인접한 삼각형을 '이웃 삼각형', '인접 삼각형' 등으로 부른다.
각 변마다 1개씩 총 3개의 인접 삼각형이 존재할 수 있으므로, 삼각형 리스트로 인접을 표현할 때 6n의 버텍스로 n개의 삼각형을 정의할 수 있다.
그러면 3개의 버텍스로 삼각형 그 자체를 표현하고, 나머지 3개의 버텍스로는 각 변에 어떤 삼각형이 인접해있는지에 대한 정보를 저장하는데, 인접 삼각형의 버텍스 중 하나를 저장하여 인접을 표현한다.
이런 인접성을 Geometry Shader 단계에서 사용된다.
GS는 인접성 데이터를 사용하여 주변 지오메트리를 파악하고, 그에 기반한 테셀레이션, 그림자 효과, 실루엣 강조 등의 특수한 알고리즘을 수행한다.
지오메트리 셰이더가 인접 삼각형 정보를 이용하기 위해서, 버텍스/인덱스 버퍼에 삼각형 그 자체에 더하여 인접삼각형의 정보를 제출해야한다. 그리고 파이프라인이 버텍스 버퍼에서 인접 삼각형임을 알 수 있도록D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST_ADJ 토폴로지를 지정해야 한다.
인접성을 나타내는 인접 프리미티브 버텍스는 GS의 알고리즘에만 활용될 뿐, 실제로 그려지지 않는다는 점에 유의하라.
인접성은 삼각형 리스트만 가질 수 있는 것은 아니며, 라인 리스트, 라인 스트립, 삼각형 스트립 프리미티브도 포함할 수 있다. 자세한건 문서를 참고
7. Control Point Patch List
D3D11_PRIMITIVE_TOPOLOGY_N_CONTROL_POINT_PATCHLIST 토폴로지 타입은 버텍스 데이터를 N개의 Control Point가 있는 패치 리스트로 해석해야 함을 나타낸다. 이는 렌더링 파이프라인의 테셀레이션 단계에서 사용되므로, 이에 대한 논의는 나중에 하도록 한다.
8. Indices
이미 언급했듯, 삼각형은 견고한 3D 객체의 기본 구성 요소이다.
다음 코드는 삼각형 리스트를 사용하여 사각형과 팔각형을 구성하는 데 사용되는 버텍스 배열을 보여준다.

삼각형의 버텍스를 지정하는 순서는 중요하며 이를 와인딩 순서라고 한다. (Winding Order)
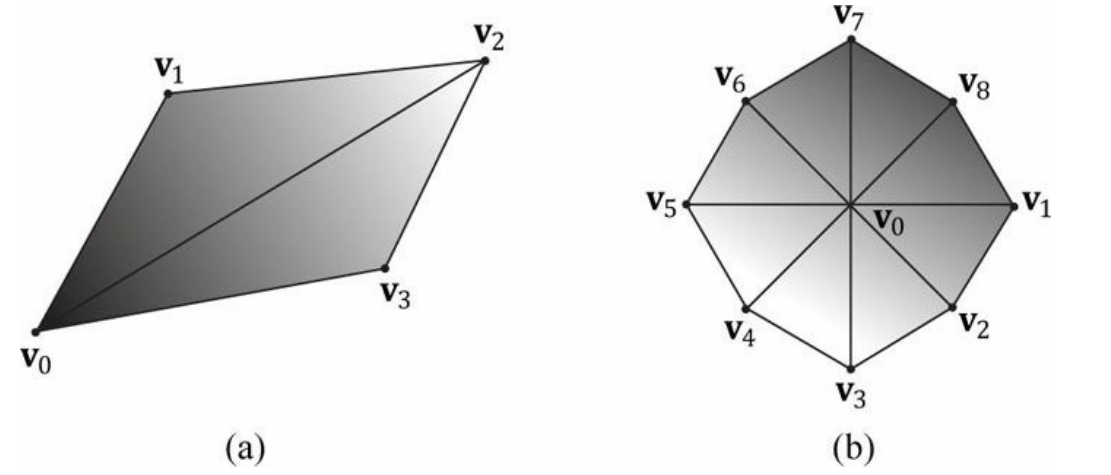
위 정점들로 정의된 폴리곤은 위와 같다.
위 그림에서 볼 수 있듯 3D 객체를 구성하는 삼각형은 많은 동일한 버텍스를 공유한다.
(a) 사각형은 두 삼각형이 정점 v2, v0를 공유하고
(b) 팔각형은 모든 삼각형이 정점 v0를 공유하며, 인접한 삼각형 끼리 정점을 공유하고 있다.
일반적으로 모델이 복잡해질수록 중복되는 버텍스의 수는 증가한다.
위 코드 대로라면, 동일한 버텍스를 버텍스 버퍼엥 중복하여 채우고 있다.
이를 피해야 하는 두 가지 이유가 있다.
1. 메모리 사용량 증가 (버텍스는 단순한 구조체가 아니라, 복잡한 데이터 뭉치이기에 버텍스 하나하나의 크기는 크다.)
2. 계산량 증가 (버텍스 당 소모되는 계산량은 무시할 수 없다.)
삼각형 스트립은 기하학이 스트립 모양으로 구성될 수 있는 경우에 중복 버텍스 문제를 해결하는 데 도움이 될 수 있다.
그리나 삼각형 리스트는 더 유연하게 사용될 수 있기 때문에.. 삼각형 리스트에서 중복 버텍스를 제거하는 방법을 생각할 필요가 있다.
해결책은 인덱스를 사용하는 것이다. 작동 방식은 다음과 같다.
버텍스 리스트와 인덱스 리스트를 만든다.
버텍스 리스트는 다각형을 이루는 모든 버텍스로 구성되고
인덱스 리스트는 버텍스가 삼각형을 형성하기 위해 어떻게 결합되어야 하는지를 정의한다.
즉, 위 다각형을 정의하는 코드는 인덱스 리스를 사용하면 매우 간단하게 정리할 수 있게 된다.
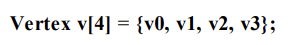
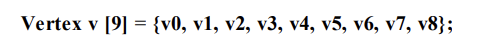

인덱스 리스트의 세 요소마다 하나의 삼각형을 정의한다.
그러면, 그래픽 카드가 버텍스에 대한 연산을 중복없이 처리하고
인덱스 리스트를 사용하여 버텍스를 결합하여 삼각형을 형성할 수 있다.
이것은 '중복'을 인덱스 리스트로 옮긴 것인데, 이는 기존 방식보다 더 효과적이다.
인덱스는 단순히 정수이기 떄문에 버텍스 만큼 메모리를 많이 잡아먹지 않을 뿐더러, 적절한 버텍스 캐시 순서가 있다면, 그래픽 하드웨어는 중복된 버텍스를 자주 처리할 필요가 없다.
Vertex Shader Stage (VS)
인풋 어셈블리(IA) 단계에서 버텍스 버퍼와 인덱스 버퍼가 조립된 후, 버텍스들은 버텍스 쉐이더(VS) 단계로 전달된다.
버텍스 쉐이더는 버텍스를 입력받아 다시 버텍스를 출력하는 단계이다. 그려지는 모든 버텍스들은 버텍스 쉐이더를 거치게 된다.

버텍스 쉐이더는 버텍스들을 (특수한 방법으로) 계산하는 하나의 함수로 생각할 수 있으며, 위와 같은 코드가 하드웨어에서 실행되는 것으로 개념화할 수 있다.
버텍스 쉐이더 함수는 우리가 구현하는 것이지만, GPU가 각 버텍스마다 실행하기 때문에 매우 빠르다.
Transformation, Lighting, Displacement mapping 과 같은 다양한 특수 효과는 버텍스 쉐이더에서 처리할 수 있다. 우리는 입력 버텍스 데이터에 접근할 수 있을 뿐만 아니라, 변환 행렬, 조면과 같은 GPU 메모리에 저장된 텍스처 및 기타 데이터에도 접근할 수 있다.
이 책에서는 다양한 버텍스 쉐이더의 예제를 많이 보게 될 것이므로, 이를 통해 버텍스 쉐이더로 무엇을 할 수 있는지 잘 이해할 수 있을 것이다.
첫 번쨰 코드에서는 버텍스 쉐이더를 사용하여 버텍스를 변환하는 데만 집중할 것이다.
1. 로컬 공간과 월드 공간
(책과 내용은 다르지만, 동일한 개념을 설명합니다.)
집에 소파를 두고 싶다고 해보자. 당신은 소파를 만들어서 집에 소파를 배치해야 한다.
그러면 어떤 방식을 택하겠는가?
1. 집으로 모든 작업도구를 가져와서 배치할 위치를 정한다음 그 다리에서 소파를 만든다.
2. 작업하기 편한 작업실에서 소파를 만든다음 완성된 소파를 적절한 위치에 배치한다.
아마, 1번 방식으로 만들기보단 2번 방식으로 만드는 것이 아마도 더 편리할 것이다.
비유해보자면
집을 월드 공간 world space
작업실을 로컬 공간 local space
라고 생각할 수 있다.
로컬 좌표계는 객체에 맞게 축이 정렬된 편리한 좌표계가 된다.
3D 모델의 버텍스를 로컬 좌표게에서 정의한 다음, 그것을 원하는대로 월드 공간에 배치하면 된다.
이 작업을 수행하기 위해서는 로컬 공간과 월드 공간이 어떻게 관련되는지를 정의해야 한다.
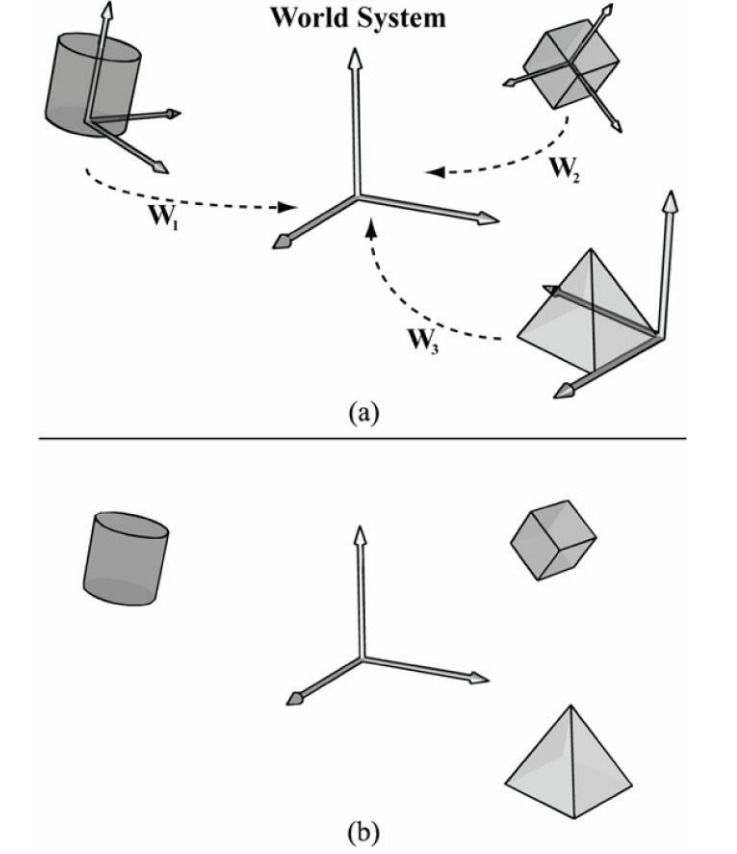
로컬 좌표계에 대한 좌표를 글로벌 좌표계로 변경하는 과정을 월드 변환 (World Transform) 이라고 하며,
변환을 구현하는 변환 행렬을 World Matrix라고 한다.
(월드 행렬은 모델링 행렬과 동일한 것이다.)
각 객체의 버텍스들은 자체적인 로컬 좌표계를 기준으로 정의된다. (이는 모델을 설계할 때 편리함을 제공한다.) 우리는 장전에 오브젝트를 배치해야 하는데, 이때 월드를 기준으로 한 오브젝트의 위치, 방향, 각도 등을 좌표 변환을 통해서 구현한다. 월드 변환을 완료하면, 객체의 버텍스들은 모두 월드 공간을 기준으로한 좌표를 가지게 된다.
만약, 객체를 직접 월드 공간에 정의하고 싶다면, 객체의 월드 행렬을 항등 행렬로 설정하면 된다.
각 모델을 자체 로컬 좌표계를 기준으로 정의하는 것은 몇 가지 이점이 있다.
1. 모델을 설계하기 쉽다. 큐브의 버텍스를 설정할 때, 큐브의 중심에 원점을 두고 축이 큐브의 면에 수직인 로컬 좌표계를 선택하면 훨씬 쉽게 버텍스를 지정할 수 있다.
2. 객체는 여러 장면에서 재사용될 수 있다, 이 경우 특정 장면에 상대적인 객체의 좌표를 하드코딩하는 것은 의미가 없다.
대신, 로컬 좌표계에 버텍스를 지정하고, 로컬 좌표계와 월드 좌표계가 어떻게 관련되는지 정의하는 것이 더 좋다.
3. 같은 객체를 장면에서 여러 번 그리지만, 각기 다른 위치, 방향, 스케일로 그릴 때, 각 인스턴스마다 객체의 버텍스와 인덱스 데이터를 복제하는 것은 비효율적이다. 대신, 로컬 스페이스에 대한 단일 사본을 저장하고, 여러 번의 객체를 그리지만, 각 경우마다 다른 월드 행렬을 사용하여 월드 공간에서 인스턴스의 위치, 방향, 및 스케일을 지정하는 것이 더 효율적이다.
(즉, 오브젝트마다 메시를 나타내는 버텍스 버퍼, 인덱스 버퍼를 복사하는 것이 아니라 버퍼를 여러번 읽는 것. 읽은 다음에 월드 변환을 수행한다.)
이를 Instancing (인스턴싱) 이라고 부른다.
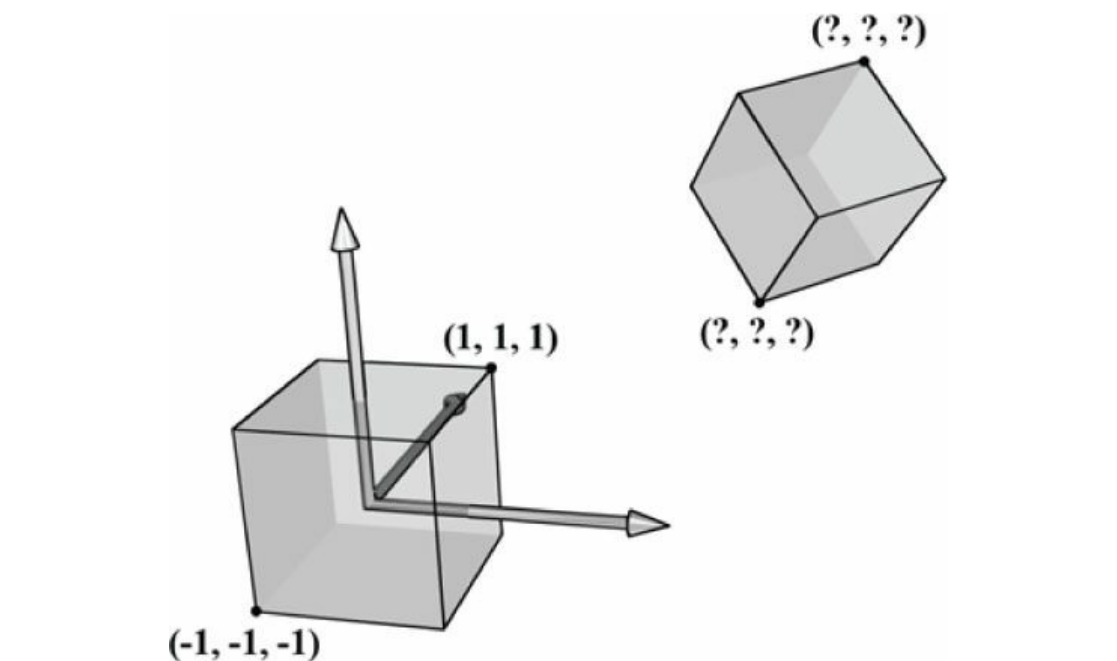
큐브가 원점에 중심을 두고 좌표계와 축이 절렬되어 있을 때, 버텍스를 매우 쉽게 지정할 수 있다.
큐브가 좌표계에 대해 임의의 위치와 방향에 있을 때 좌표를 지정하는 것은 매우 어렵다.
따라서, 모델링에 편리한 좌표계를 선택하여 그 객체를 중심으로 빌드한다.
객체의 월드 행렬은 로컬 공간을 월드 공간에 대한 좌표로 설명하는 좌표계 변환을 수행한다.
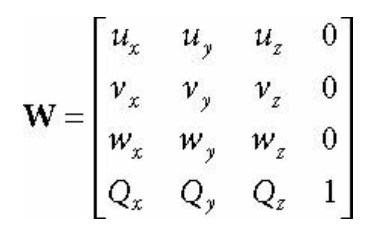
즉, 월드 입장에서 바라본 로컬 공간의 기저 벡터와 원점의 위치를 알 수 있다면
월드 행렬은 위와 같다.
월드 행렬을 구성하려면, 우리는 로컬 공간의 원점과 기저 벡터를 직접적으로 파악해야 한다.
이것은 직관적이지 않을 순 있지만, 얻어내기는 매우 쉽다.
우리는 앞서 동차 좌표계에서의 회전 행렬, 스케일링 행렬, 평행 이동 행렬을 알아보았다.
그리고 행렬의 결합법칙 또한 알아보았다.
그리고.. 이전 포스팅을 보면 아핀 결합과 좌표계 변환은 동일한 식을 가진다라는 것도 알아보았다.
그러므로 S*R*T 행렬의 결과는 월드 행렬임을 알 수 있다.
S는 스케일링 행렬
R는 로테이션 행렬
T는 트랜스레이트 행렬이다.
죄종적으로 얻어낸 행렬 W의 행 벡터는 로컬 공간의 기저 벡터 및, 월드 스페이스에 대한 로컬 좌표계 원점의 위치를 표현한다.
이 설명의 핵심은 월드 행렬을 구성하는 위해 행렬 W를 직접 계산하는 대신, 간단한 변환들의 곱으로 월드 행렬을 구성할 수 있다는 것이다. 이러한 프리미티브한 변환 (회전, 이동, 크기 변환) 각각은 매우 직관적이다.
월드 행렬인 W를 오브젝트의 버텍스 마다 곱해주면 월드 좌표계를 기준으로하는 버텍스를 얻어낼 수 있다.
(이해하는데 필요없는 설명은 많이 제거함. 결국 좌표계 변환과 아핀 변환 이야기)
2. 뷰 공간
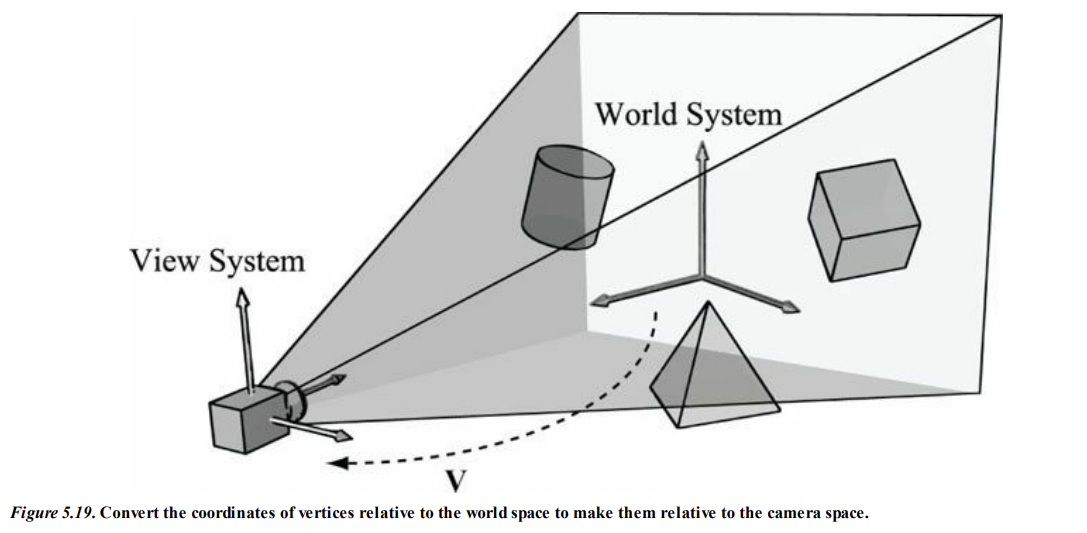
우리는 가상의 카메라를 가지고 있고, 가상 카메라를 바라보는 장면을 기준으로 2D 이미지를 생성해야 한다.
카메라는 관찰자가 세계의 어떤 영역을 볼 수 있는지 지정하며, 따라서 어떤 영역의 2D 이미지를 생성해야 하는지를 결정한다.
위 그림을 참고하자.
카메라는 원점에 위치하고 z축을 바라보고 있으며, x축은 카메라의 오른쪽, y축은 카메라의 위쪽을 향한다.
우리가 카메라를 기준으로 세상을 설명하기 위해서는 로컬 버텍스들을 월드로 변환한 다음에 카메라 좌표계를 기준으로 또 변환해야 한다.
월드 공간에서의 버텍스들을 뷰 공간으로 변환하는 것을 뷰 변환이라고 해며, 이에 대응하는 행렬을 뷰 행렬이라고 한다.
한 번 더 설명하자면
뷰 공간을 기준으로 카메라는 원점에 위치하고, Z축을 바라보고 있으며, x축은 카메라의 오른쪽, y축은 카메라의 위쪽을 향한다. 월드 공간에서는 원점을 기준으로 카메라 또한 다른 기저 벡터와 로컬 원점을 가진다. 그러므로 뷰 공간에서 월드 공간으로의 카메라 좌표 변환 행렬은 다음과 같다.
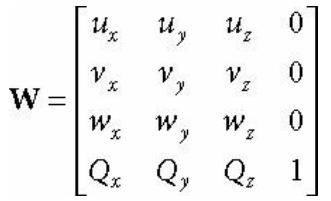
이것으 뷰 공간에서 월드 공간으로 변환하는 행렬이라면
월드 공간에서 뷰 공간으로 변환하는 행렬은 W의 역행렬일 것이다.
W = S R T 이므로 역행렬은 다음과 같다.
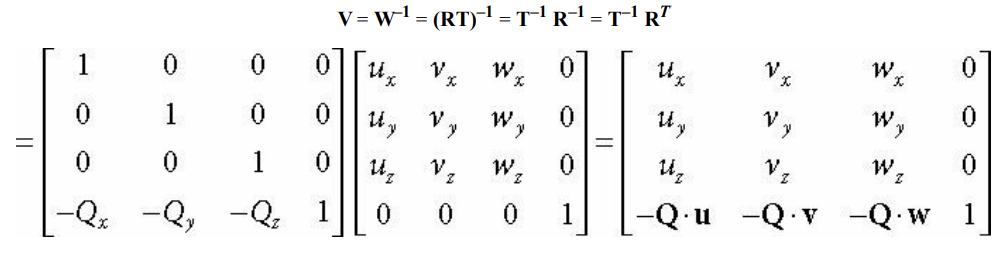
여기서 스케일링 행렬 S를 고려하지 않은 이유는 카메라는 크기 변환의 개념이 없기 때문이다.
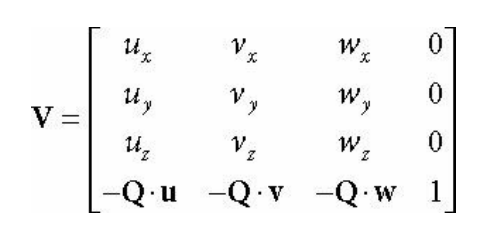
최종적인 뷰 변환 행렬은 위와 같다.
이제는 뷰 행렬을 직관적으로 얻어내는 방법을 보여주겠다.
Q를 카메라의 월드 공간 상의 위치
T를 카메라가 조준하는 점이라고 하자.
또한, j를 월드 공간에서 Up 을 나타내는 단위 벡터로 두자.
일반적으로\로는 xz 평면을 지면으로 사용하기 때문에 Up 단위 벡터는 (0, 1, 0) 이다.
하지만 이는 정의된 좌표계 시스템에 따라 달라질 수 있다. 일부 애플리케이션은 xy 평면을 지면으로 두기 때문에 z축을 위쪽 방향으로 선택한다.
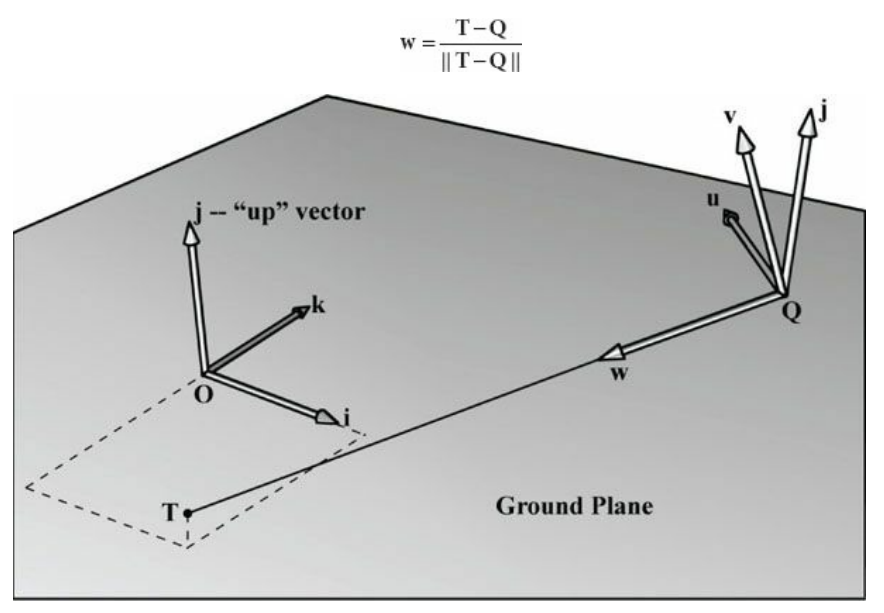
어쨌든, 시각적으로 나타내면 위 그림과 같다.
w벡터는 카메라의 로컬 z축을 나타낸다.
w벡터는 벡터의 뺄셈을 통해서 손쉽게 구해낼 수 있으며
로컬 Right 기저인 u는 j와의 외적을 통해 구해낼 수 있다.
아지막으로 로컬 Up 기저인 v는 w와 u의 외적으로 구할 수 있다.
(외적을 통한 직교화)
따라서 카메라의 위치, 카메라가 바라보는 타겟, 월드의 위쪽 방향이 주어지만, 우리는 뷰 행렬을 구성하는 데 사용할 수 있는 카메라의 로컬 좌표계를 유도할 수 있다.
(단, 카메라가 Up과 평행하게 서있는 경우에는 예외처리를 해줘야만 한다.)
DirectXMath 라이브러리에서는 방금 설명한 과정을 기반으로 뷰 행렬을 계산하기위한 함수를 제공한다.
참고로 뷰 공간은 다른 말로
view space, eye spcae, camera space 등으로 불린다. (참고)
3. 투영과 동차 클립 공간
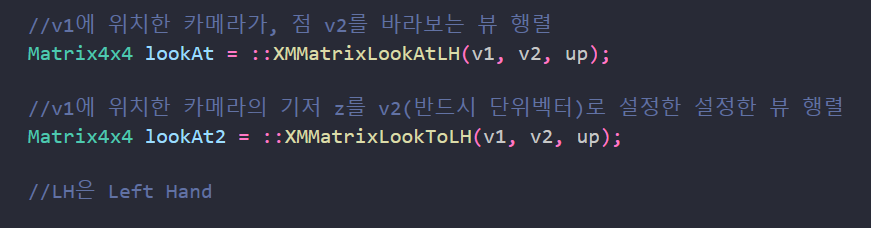
지금까지 월드에서 카메라의 위치와 방향에 대해 설명했지만, 카메라의 또 다른 구성 요소는 카메라가 보는 공간의 부피이다.
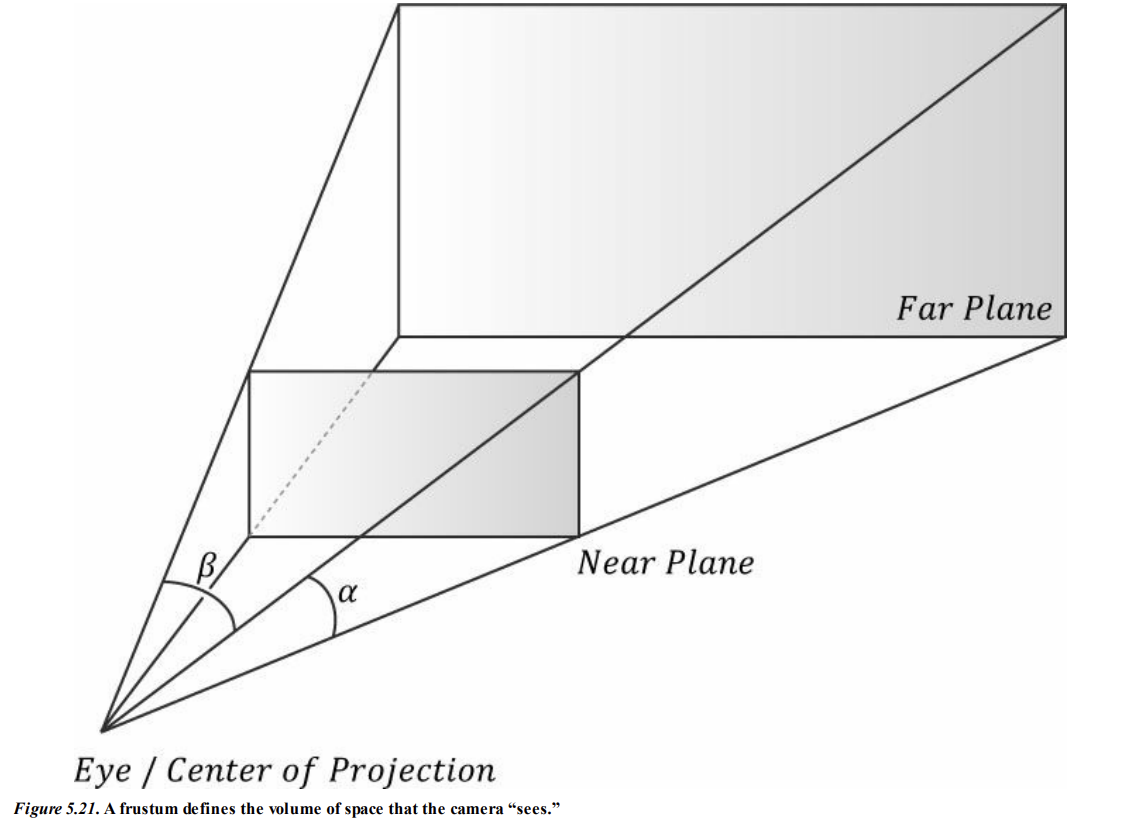
이는 가시공간(View Volume) 이라 표현하기도 하며, 피라미드의 꼭대기를 잘라냈다하여 절두체, 혹은 Frustum (프러스텀) 이라고 부른다.
프러스텀이라는 용어를 많이 사용하기 때문에 나도 프러스텀이라고 부르겠다.
프러스텀 내부의 3D 기하학을 2D 투영 창에 투영해보자.
투영은 평행선이 소실점으로 수혐하고, 객체의 3D 깊이가 증가함에 따라 투영된 크기가 감소하는 방식으로 수행되어야 한다.
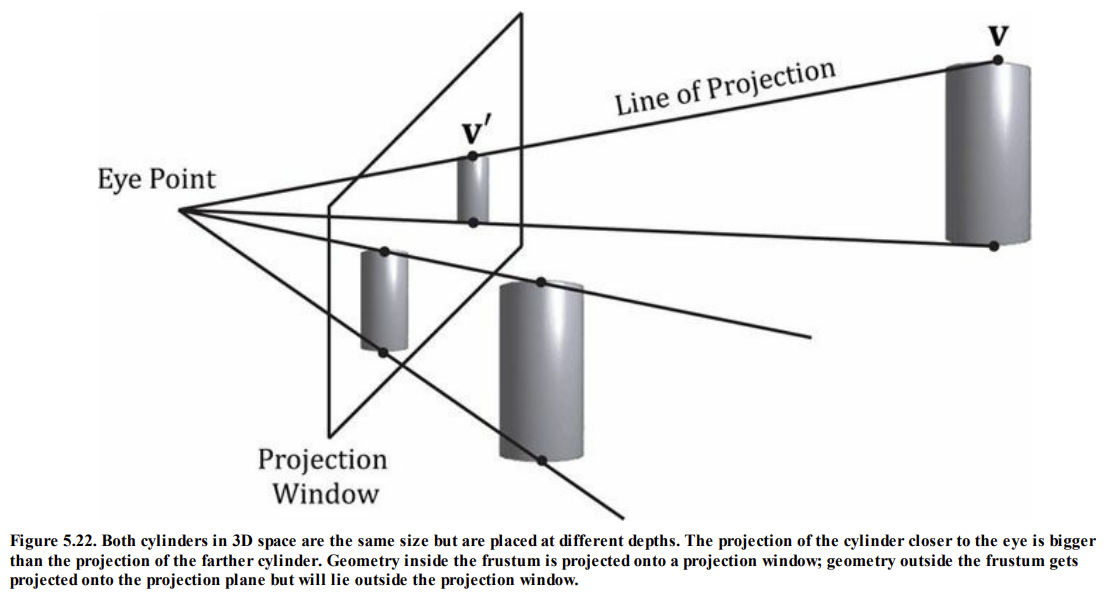
이를 원근투영이라고 하며 시각적으로 나타내면 위 그림과 같다.
3D 공간의 두 실린더는 크기가 같지만, 카메라에서 멀수록 그 크기가 더 작게 투영된다.
카메라 전면에는 투영 평면이라는 가상의 윈도우가 존재하며
투영 평면보다 가까운 물체는 더 크게
투영 평면보다 더 먼 물체는 더 작게 묘사된다.
버텍스에서 시점까지의 선을 버텍스의 투영선이라고 부른다.
원근 투영 변환은 3D 버텍스 v를 2D 투영 평면과 그 투영선이 교차하는 지점 v`로 변환하는 것을 의미한다.
이때 v'는 v의 투영이라고 한다.
3D 객체의 투영은 객체를 구성하는 모든 버텍스의 투영을 의미한다.
4. 프러스텀 정의
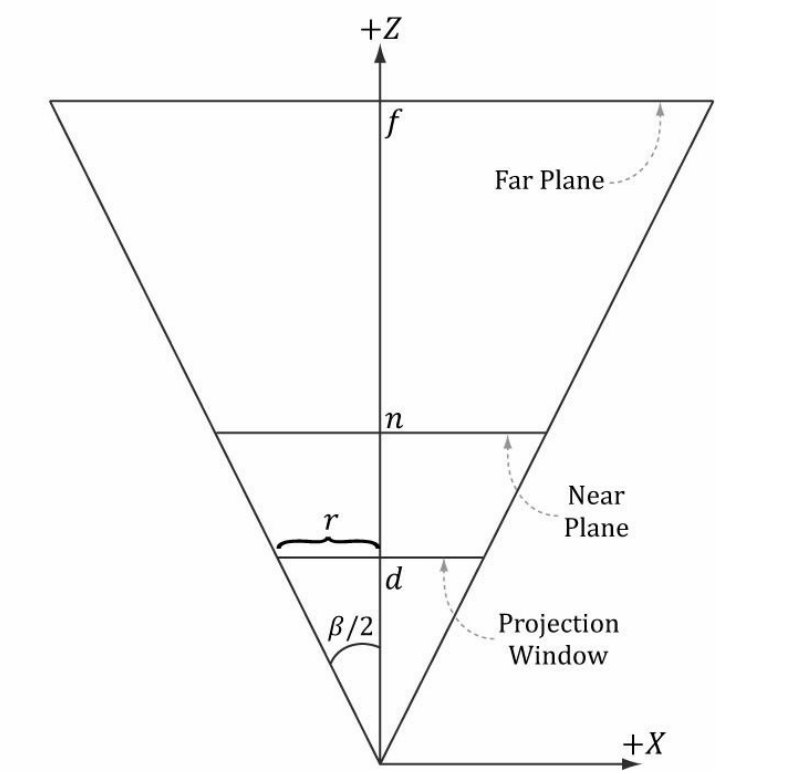
뷰 공간에서 프러스텀을 정의할 때, 설정해야할 변수는 4가지이다.
1) 근평면 n (near plane)
2) 원평면 f (far palne)
3) 수직 시야각 α (화각이라고도 한다.)
4) 종횡비 r
뷰 공간에서 근평면과 원평면은 단순히 카메라에서 표시할 가장 가까운 면과 먼 면을 의미한다.
xy-평면과 평행하기 때문이다.
종횡비는 r = w/h 로 정의된다. w는 투영 창의 너비고 h는 투영 평면의 높이다.
투영 평면은 본질적으로 뷰 공간에서 장면의 2D 이미지이다.
투영 평면에 만들어진 이미지는 백 버퍼에 그대로 매핑된다.
그러나, 투영 평면의 크기와 백 버퍼의 크기는 같을 필요가 없다. 이 둘의 종횡비만 같다면, 투영 평면에 투영된 정점들의 좌표를 스칼라 배만큼 늘려서 백 버퍼의 크기와 일치시켜주면 되기 때문이다.
그렇기에 투영 평면의 종횡비와 백 버퍼의 종횡비는 동일해야 하며, 이 둘의 종횡비 불일치는 비균일한 스케일링을 발생시켜 왜곡을 일으킬 것이다. (원이 타원으로 늘어날 수 있다.)
우리는 아마도, 백 버퍼의 크기를 알고있을 것이다. 예를 들어, 백 버퍼의 크기가 800 x 600 이라면
종횡비는 r = 800/600 이다.
이 종횡비를 그래도 투영 평면에 사용할 수 있다.
이런 특성 덕분에, 종횡비만 동일하다면 투영 평면의 크기는 중요하지 않다.
그러므로 투영 평면의 높이는 계산의 편의성을 위해 [-1, 1] 의 범위를 가지도록 설정한다.
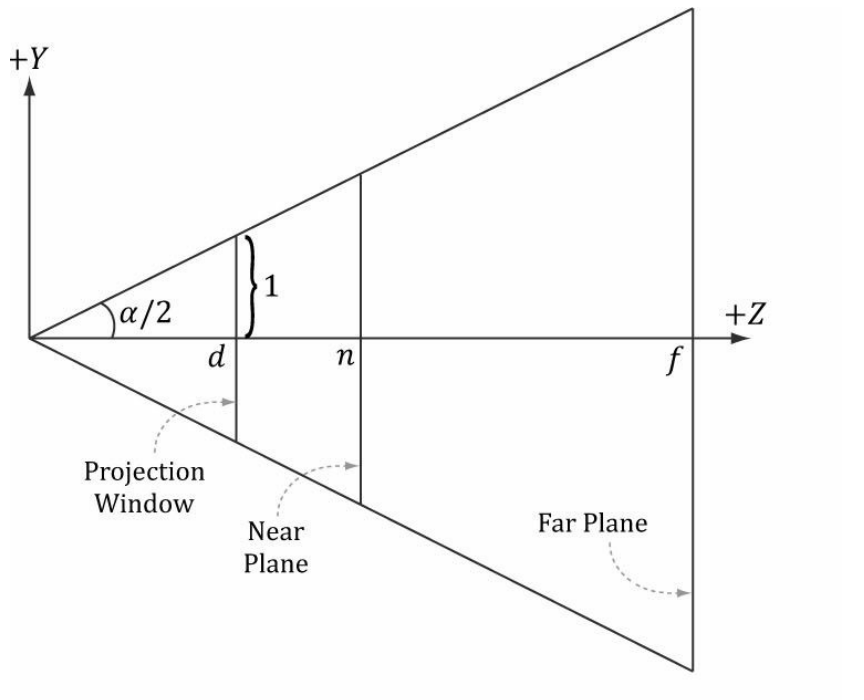
수평 시야각을 β로 표시하며, 이는 수직 시야각 α와 종횡비 r에 의해 결정된다.
뷰 공간의 절두체를 옆에서 보도록 하자.
일반적으로 투영 평면은 가로 세로의 길이가 [-1, 1]을 가진다고 했다.
그러면 투영평면의 높이의 절반은 1일 것이다.
이것과 수직 시야각 α를 이용하면 초점거리 d를 구할 수 있게 된다.
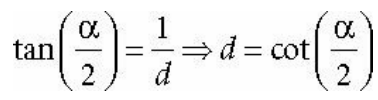
높이가 2라고 하면
너비는 2에다가 종횡비 r를 곱한 2r이다.
역삼각함수를 이용하면 수평 시야각 β를 구할 수 있다.
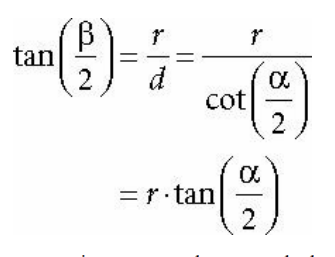
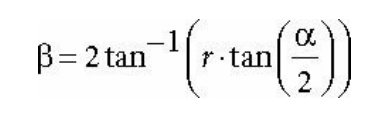
따라서 세로 시야각 a와 종횡비 r을 알면 언제나 가로 시야각 β를 구할 수 있다.
5. 정점 투영
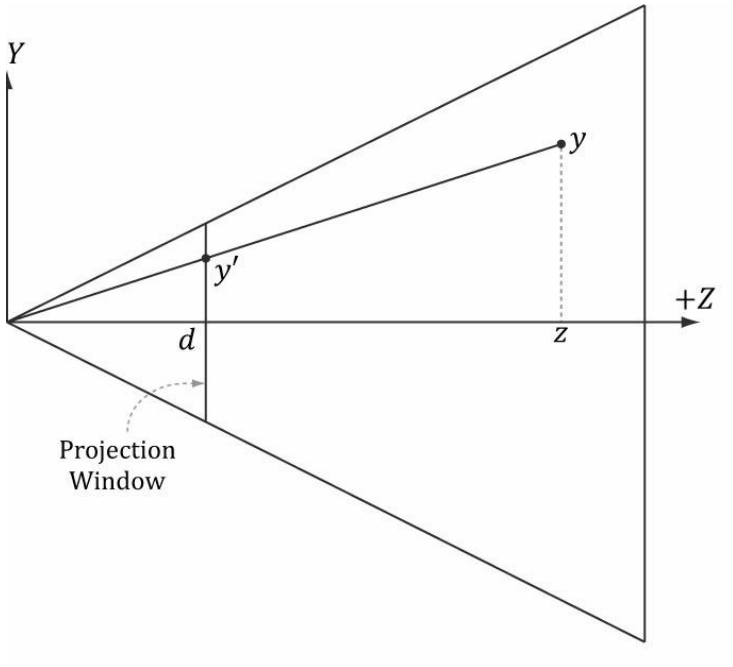
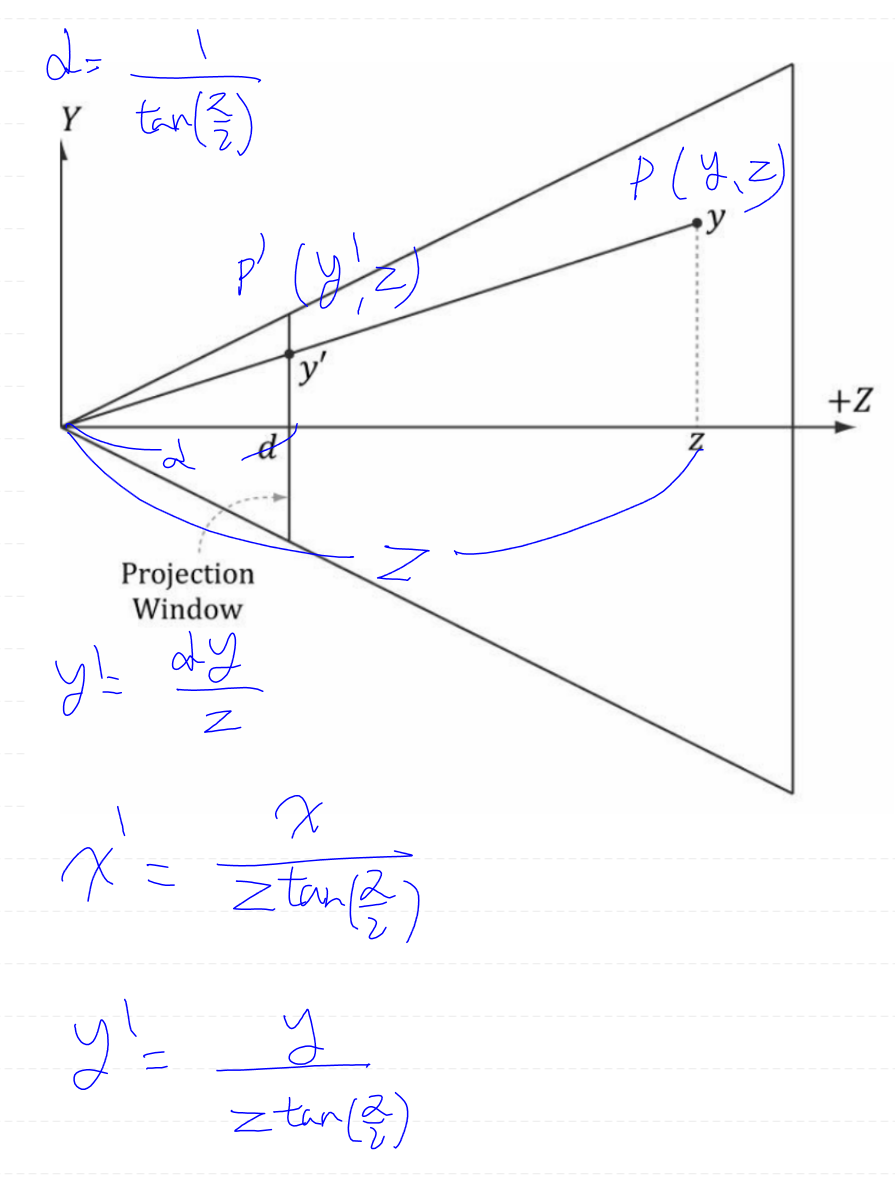
이제 정점을 투영해보자.
원점에서 정점 y까지의 직선과 투영 평면이 접하는 점을 y'라고 하자.
이는 닮음 삼각형을 이용하면 손쉽게 구할 수 있다.
투영 공간에 정의된 P'에 대해서 다음 부등식이 성립하면 뷰 공간에 있는 점 P(x, y, z)은 절두체 내부에 존재한다고 볼 수 있다.
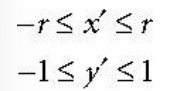
더하여 점 P에 대해서 아래 부등식 또한 동시에 만족해야한다.
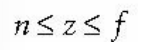
6. 정규화 장치 좌표 (Normalized Device Coordinates, NDC)
이전 섹션에서 보았듯 투영된 점들의 좌표는 뷰 공간에서 계산된다.
뷰 공간에서 투영 평면의 높이는 2이고, 종횡비에 따라 폭은 2r이다.
해당 좌표계의 문제점은 종횡비에 대한 정보가 있어야 한다는 것이다.
이 말은 하드웨어에게 종횡비를 알려주어야 한다는 것을 의미하며,
이는 지금 파이프라인 단계에선 알려주기는 껄끄럽다.
왜냐면 하드웨어가 윈도우와 관련된 작업을 수행한는 것은 더 나중의 일이기 때문이다.
이 종횡비에 대한 의존성을 제거할 수 있다면 더 편할 것이다.
해결책은 투영된 x-좌표를 [-r, r] 구간에서 [-1, 1]로 스케일하는 것이다.
이런 가로 세로 [-1, 1] 범위를 가지는 정사각형 좌표계를 정규화 장치 좌표 NDC 공간이라고 하며, 점 (x, y, z)이 뷰 프러스텀 내에 있기 위해서는 다음과 같은 부등식이 성립해야한다.
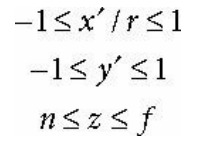
해당 공간은 뷰 공간과는 다르다.
말 그대로 좌우로 찌끄러뜨린 형상을 하고 있기 때문에
ndc 좌표계에서 x축의 1은
뷰 공간에서 r (종횡비) 와 동일하다.
관계식은 다음과 같다.
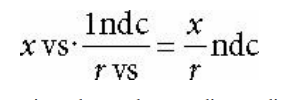
(단순하게.. 뷰 공간 x를 ndc x'로 바꾸려면 종횡비를 나누면 되고, ndc x를 뷰 공간 x'로 바꾸려면 종횡비를 곱하면 된다.)
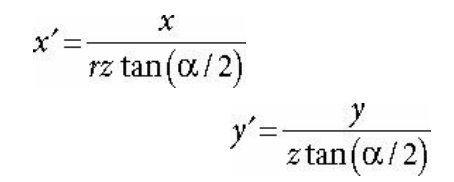
우리는 투영 공식을 수정하여 위와같은 투영 식을 만들어낼 수 있다.
y 좌표 투영 식은 기존과 동일하고
x 좌표 투영 식은 추가적으로 종횡비를 나눠주고 있다.
이를 시각적으로 생각해보자. NDC 좌표계는 정사각형이며, 결국 나중에 종횡비 만큼 가로를 늘려줄 것 이다.
그러면 기존 투영식을 계속 사용했을 시, 원이 가로가 긴 타원형태로 늘어나게 될 것이다.
그러므로 NDC 좌표계에서는 세로가 긴 타원형태로 종횡비 만큼 쪼그라들게 한다면, 나중에 종횡비 만큼 늘렸을 때 다시 원을 만들어 낼 것이다.
따라서 우리는 투영 결과, 투영 평면은 [-1, 1] 범위를 가지는 정사각형 영역인 정규화 장치 좌표계를 사용하도록 한다. 행렬식에 직접 종횡비 수식을 넣어줄 것이기에 하드웨어는 종횡비를 알 필요없다.
우리는 항상 NDC 좌표계를 이용해야 하는데, 파이프라인 자체가 NDC 공간의 투영 버텍스를 입력으로 원하기 때문이다. (그래픽 하드웨어와 라이프러리가 그렇게 할 것이라고 가정하고 동작한다.)
현재까지 작성한 내용을 보면, 굳이 NDC 좌표계를 사용하는 것은 설득력이 떨어질 수 있다.
사실 투영까지만 생각하면 NDC 좌표계를 사용하지 않아도 된다. 막상 투영 식만 봐도 종횡비에 대한 정보는 포함되지 않는다.
그러나 이후에 문제이다. 만약 기존 종횡비가 적용된 투영 평면을 계속 사용한다면 이후에 클리핑, 뷰포트 변환 등.. 을 수행할 때, 식이 조금 더 복잡해지게되고 하드웨어는 종횡비에 대한 정보를 계속 알아야 한다. 이는 비효율적이다.
가로를 [-r, r] 에서 [-1, 1]로 바꿔주기만 하더라도 이후 알고리즘을 수행함에 있어 식이 훨씬 간단해진다.
사실상 계산의 복잡도를 낮추기 위해서 NDC 좌표계를 사용하는 것이다.
더하여 하드웨어 자체로 NDC 좌표계에서 연산하도록 설계되어 있고, 그래픽 라이브러리도 그렇게 가정하고 알고리즘을 수행하기 때문에, 무조건적으로 NDC 좌표계를 이용할 수 밖에 없다.
7. 투영 행렬
행렬 곱을 위해, 투영 변환을 행렬로 표현하고자 한다.
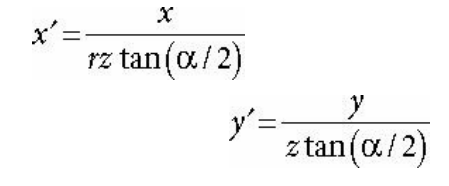
책에는 매우 난잡하게 설명되어 있어서 간단하게 설명을 바꾼다.
뷰 공간에 있는 버텍스는 4D 좌표를 가진다.
4D 좌표를 가지는 이유는.. 로컬 공간에 있는 3D 좌표에 월드 행렬, 뷰 행렬을 곱하면서 4D 동차좌표계로 변환되었기 때문이다.
투영 방정식을 보자.
종횡비 r과 수직 시야각 a는 변하지 않는 상수이다.
그러나 z는 버텍스마다 다른 값을 가지고 있다.
이 뜻은 1000개의 버텍스가 존재한다면, 1000개의 다른 투영방정식이 필요하다는 의미이다.
이는 계산 복잡성을 높인다.
이 방식보다는 z는 나중에 나눠주고, 상수로만 방정식을 구성하면 하나의 방정식으로 모든 버텍스를 계산할 수 있다.
단, 본질적으로 투영 방정식과 차이가 있기에.. 해당 방정식을 버텍스에 곱하면 투영 평면이 아닌, 다른 공간으로 변환된다. 이러한 공간을 클립 공간이라고 말한다.
더하여, 변수인 z가 분모에 위치하기 때문에 위 식은 선형성을 가지지 않는다.
역수 함수는 가산성과 동차성을 만족하지 못하기 때문이다.
결국 계산의 효율성 때문에 식은 항상 선형성을 가지게 하여 행렬 꼴로 바꿔주는 것이 좋으며
선형성을 만족시키기 위해서 그리고 계산 복잡도를 낮추기 위해 z를 분리해 줘야만 한다.
책에서는 이를 선형 부분(클립 공간으로 투영)과 비선형 부분(z 역수곱)을 분리한다. 라고 표현한다.
그러면 x, y 좌표를 클립 공간으로 투영하는 투영 방정식을 구해보자.
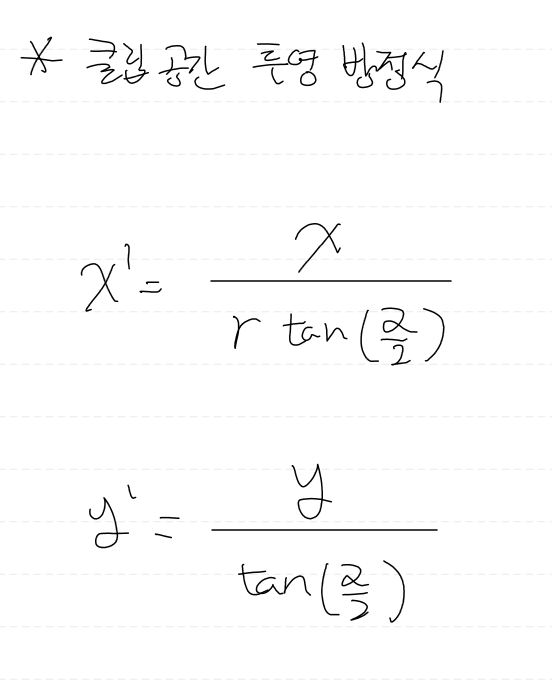
이제 이를 행렬 형태로 표현해보자.
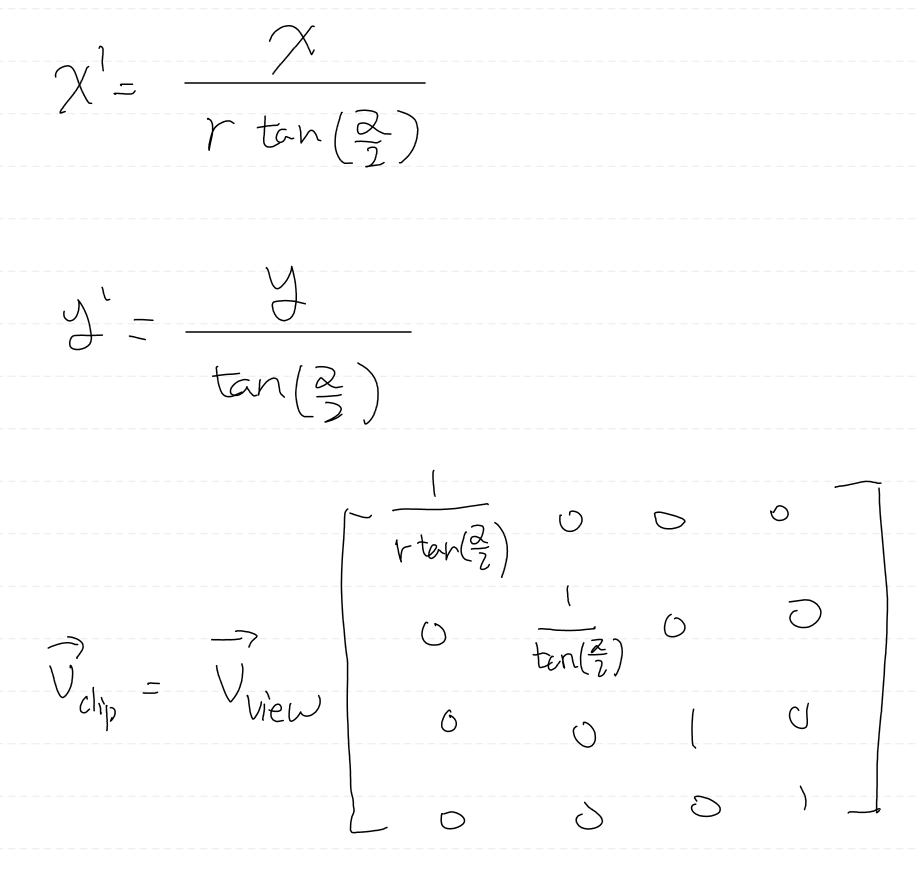
그러면 위와같은 투영행렬을 만들 수 있다.
위 식은 책에 있는 식과 다르지만, 최종적으로는 같아질 것이다.
최종적으로 NDC 좌표로 버텍스를 변환하기 위해서 각 좌표를 z로 나누어 비선형 변환을 완료해야 최종적인 투영이 완료된다. 이때, z값은 0보다 커야하는데 이러한 접은 Clipped 될 것이다.
때때로 최종적으로 z값을 나눠주는 것을 원근 나누기(Perspective Divide) 또는 동차 나누기(Homogeneous Divide) 라고 한다.
8. 정규화된 깊이 값
앞서 깊이에 대한 이야기를 하였고, 깊이는 일반적으로 [0, 1] 의 범위를 가진다. (이는 DirectX의 표준이다.)
깊이는 z값과 매우 유사하고, z값을 이용하여 객체의 깊이를 구해야 한다.
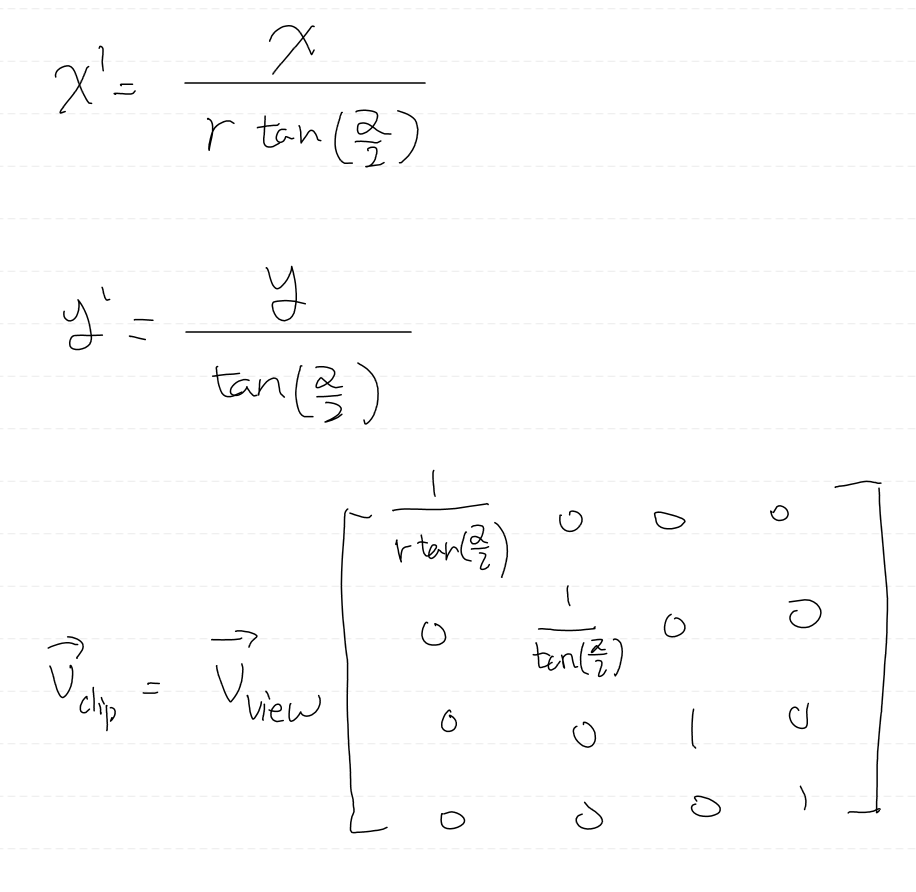
이 행렬을 통해서 투영 뿐만 아니라 깊이 값 정규화도 수행할 수 있다.
1행은 x값 투영
2행은 y값 투영
3행은 깊이 값 정규화
4행은 클립 좌표계 -> NDC 좌표계 변환을 위한 z값 보존
그러면 다음과 같이 정리할 수 있다.
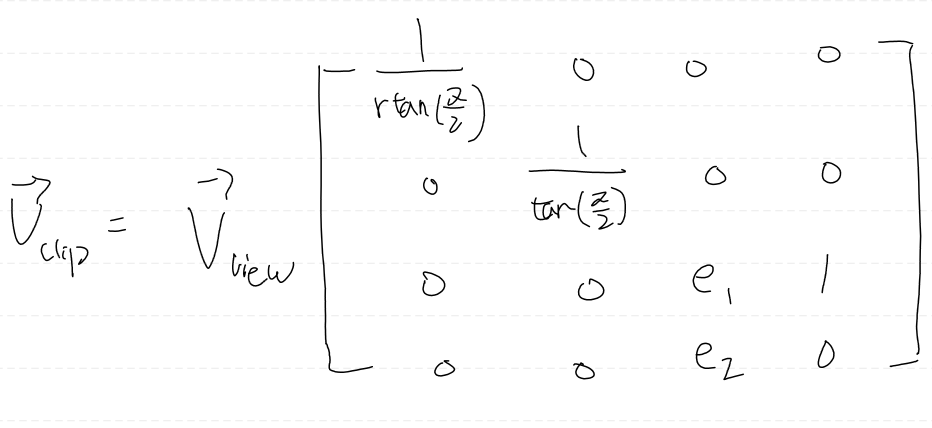
e1는 z값을 [0, 1] 범위로 선형적으로 스케일링 하는 역할을 수행한다.
그러나 원근 변환을 수행 후에 z값을 추가적으로 나눠줘야하기 때문에 e2라는 오프셋을 추가해야한다.
3열의 첫 번째, 두 번째 요소가 없는 이유는 x값과 y값은 깊이에 영향을 미치지 않기 때문이다.
그러면 깊이 z는 최종적으로 다음과 같은 방정식으로 구할 수 있다.

이제 e1, e2를 구해보자.
먼저, 뷰 공간에 z = n 인 점이 있다고 해보자.
해당 좌표는 클립 좌표로 변환했을 때 0이 나와야 한다.
더하여, 뷰 공간에 z = f 인 점이 있다고 해보자.
해당 좌표는 클립 좌표로 변환했을 때 f가 나와야 한다.
(그러면 최종 NDC 좌표로 변환했을 때, 최대 깊이인 1이 나온다.)
그러면 2개의 방정식이 나오고
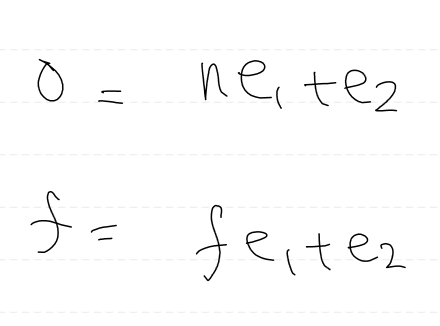
이 연립 방정식을 풀면 e1, e2값을 구할 수 있다.
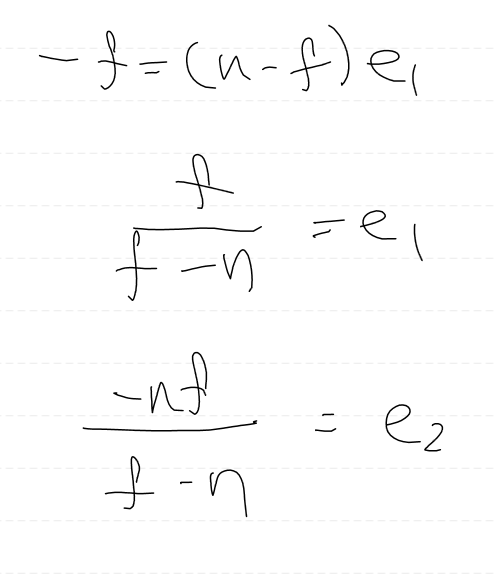
그러면 최종적인 원근 투영 행렬을 얻어낼 수 있다.
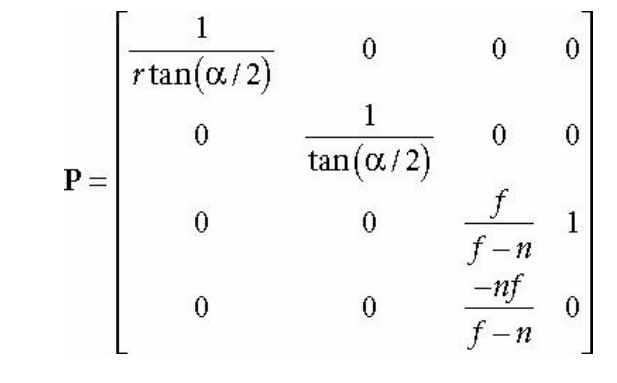
* 번외, 다른 방식으로도 e1, e2를 구해보자. (책에 소개된 방식)
우리는 뷰 공간에서의 z좌표 [n, f]를 NDC 좌표로 변환했을 때, [0, 1]로 매핑해야 하며, 깊이 순서를 보존하는 함수 g(z)를 구성해야 한다.
매개변수 z는 뷰 공간의 z좌표이고, 출력값은 NDC 좌표의 깊이이다.
함수가 순서를 보존하기 때문에 z1 < z2 라면 g(z1) < g(z2) 가 된다.
이는 어떤 깊이 값을 입력하더라도 두 깊이 값 사이의 깊이 관계는 그대로 유지되어, 정규화된 깊이를 올바르게 비교할 수 있게된다는 의미이다.
그러면, 원근 투영 행렬을 통해 얻어낸 클립 공간의 z값을 보자.
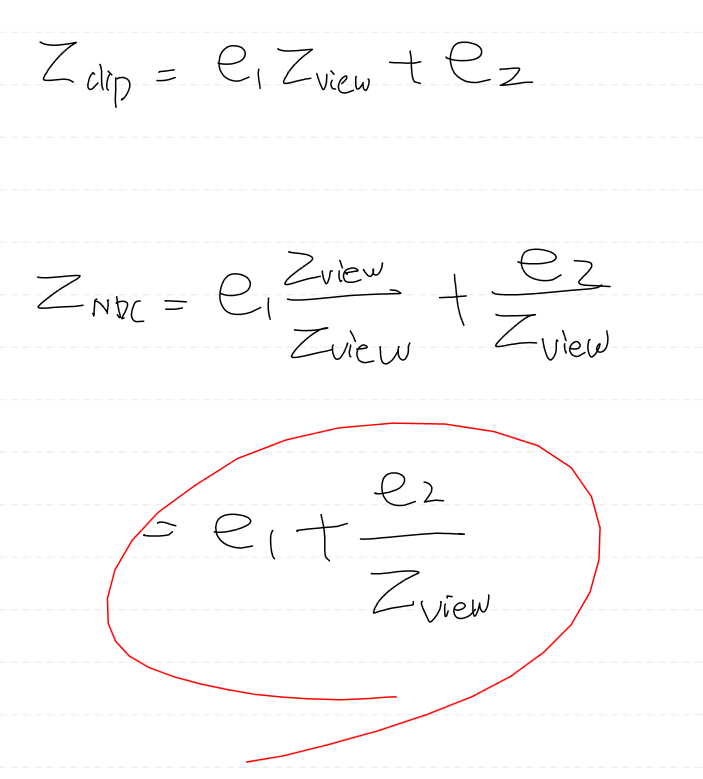
아래 빨간색 등식이 곧 g(z)를 의미한다.
그러면 g(n) = 0 이어야 하고
g(f) = 1 이어야 한다.
한 번 구해보자
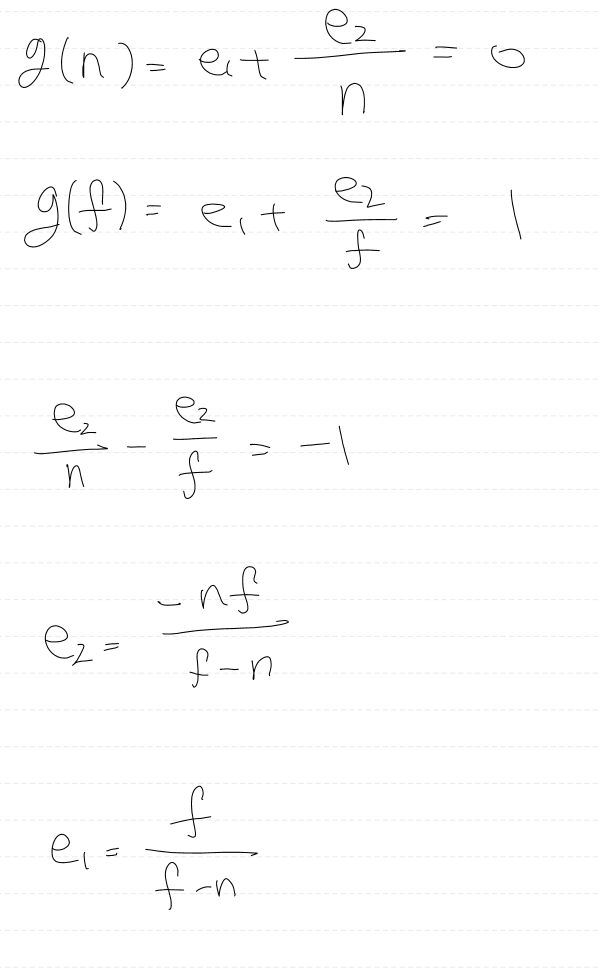
앞서 구한 방식과 동일하다!
최종적은 g(z)의 식을 보면 이러한 꼴이 된다.
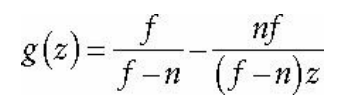
z가 분모에 덩그러니 남아있는 것이 뜻하는 것은 무엇을까?
이는 g(z) 함수의 그래프를 보면 좀 더 직관적으로 알 수 있다.
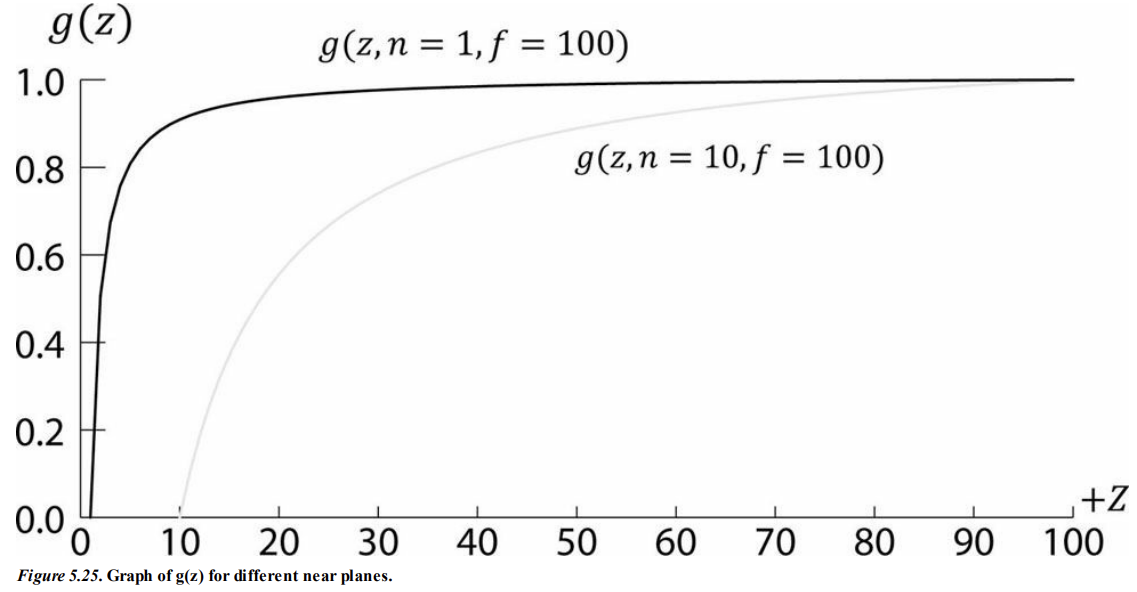
g(z)의 그래프는 급격하게 증가하는 함수를 보이고 있는데,
이는 깊이 범위 [0, 1] 의 대부분은 근평면에 가까운 객체에 소모한다는 것이다.
그러면 원평면에 근접한 객체들은 깊이 범위의 매우 작은 집합에 매핑되게 된다.
이는 깊이 버퍼의 정밀도 문제를 야기할 수 있다.
컴퓨터는 유한한 숫자 표현만이 가능하기에, 원평면에 있는 물체들의 사소한 깊이 차이는 구분할 수 없을 수도 있다.
일반적인 조언은 깊이 정밀도 문제를 최소화하기 위해 근평면과 원평면을 가능한 가깝게 설정하는 것이다.
투영 행렬을 곱한 후, 원근 나누기를 하기 전까지는 객체가
동차 클립 공간, 혹은 투영 공간에 있다고 한다.
원근 나누기을 한 후에야 정규화된 장치 좌표(NDC)에 있다고 표현한다.
9. XMMatrixPerspectiveFovLH
참고로 Fov는 화각을 나타내는 (일반적으로는 화각인데 맥락상 수직 시야각 a라고 이해하는 게 맞을 듯 하다.) 단어이다.
(다이렉트 X는 기본적으로 수직 시야각을 기본적으로 사용하는 듯 하다.)
Field Of View
LH는 왼손 좌표계를 나타내는 단어이다.
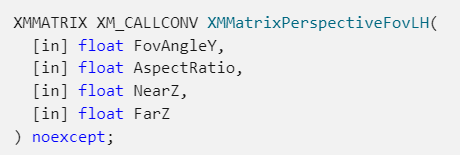
함수의 정의
참고로 근평면 Z값과 원평면 Z값은 (당연하겠지만) 뷰 공간에서 평가한 값이다.
Tessellation Stage
테셀레이션은 메시의 삼각형을 세분화하여 새로운 삼각형을 추가하는 것을 의미한다. 이러한 새로운 삼각형은 새로운 위치로 이동되어 더 정교한 메시 세부사항을 만들 수 있다.
테셀레이션에는 여러가지 이점이 있다.
1. 카메라 가까이에 있는 삼각형은 더 많은 디테일을 추가하기 위해 테셀레이션되고,
카메라에서 멀리 떨어진 삼각형은 테셀레이션되지 않은 레벨 오브 디테일(LOD) 메커니즘을 구현할 수 있다.
이 방식으로 추가 디테일이 눈에 띌 곳에만 더 많은 삼각형을 사용한다.
2. 더 간단한 로우 폴리 메시를 메모리에 유지하고, 필요한 경우 실시간으로 추가 삼각형을 추가하여 메모리를 절약한다.
3. 애니메이션과 물리 연산을 더 간단한 로우폴리 메시에서 수행하고, 렌더링에만 테셀레이션된 하이폴리 메시를 사용한다.
테셀레이션 단게는 Direct3D 11에 새롭게 추가된 기능으로, GPU에서 지오메트리를 테셀레이션할 수 있는 방법을 제공한다.
DX11 이전에는 테셀레이션을 구현하려면 CPU에서 작업을 수행한 다음, 새로운 테셀레이션된 지오메트리를 GPU로 다시 업로드하여 렌더링해야 했다. 그러나 CPU 에 테셀레이션 계산 작업을 부과하게 되는 것은 느리기에, 이전 에는 실시간 그래픽스에서 테셀레이션 방법이 많이 사용되지 않다가, Direct3D 11에 와서 하드웨어적으로 테셀레이션을 수행할 수 있게되자. 선택적으로 사용할 수 있는 기술이 되었다.
이는 13장에서 다룰 예정이다.
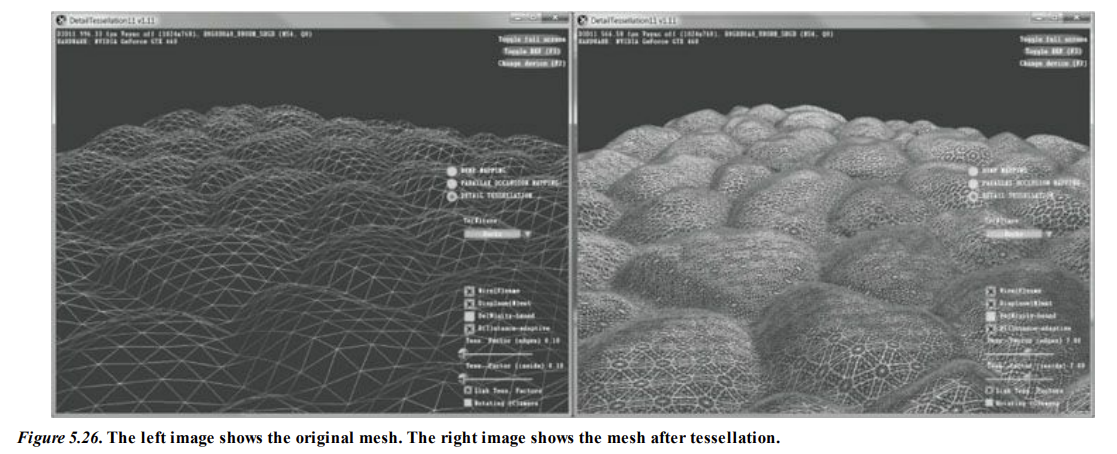
왼쪽은 테셀레이션이 적용되기 전의 메시
메시의 삼각형이 크고, 간단하며 세부적인 디테일이 부족함
테셀레이션 실행 후, 삼각형이 더 세밀하게 분할되어, 원본 메시보다 더 많은 삼각형을 포함하고 있다.
이것이 LOD (Level Of Detail) 기술이다.
Geometry Shader Stage (GS)
GS 단계는 선택적이며, 11장까지는 사용하지 않으므로 여기서는 간단하게 설명한다.
GS 는 전체 도형(primitive)을 입력으로 받는다. 예를 들어, 삼각형 리스트를 그리는 경우, 지오메트리 셰이더의 입력은 삼각형을 정의하는 세 개의 정점이 된다.
지오메트리 셰이더의 주요 장점은 지오메트리를 생성하거나 제거할 수 있다는 것이다.
예를 들어, 입력된 도형이 하나 이상의 다른 도형으로 확장될 수 있으며, 지오메트리 셰이더는 특정 조건에 따라 도형을 출력하지 않도록 선택할 수 있다.
이는 버텍스 쉐이더와 대조되는데, 버텍스 쉐이더는 정점을 생성할 수 없으며, 하나의 정점을 입력으로 받아 하나의 정점을 출력한다.
지오메트리 쉐이더의 일반적인 예로는 점을 사각형으로 확장하거나, 선을 사각형으로 확장하는 것이다.
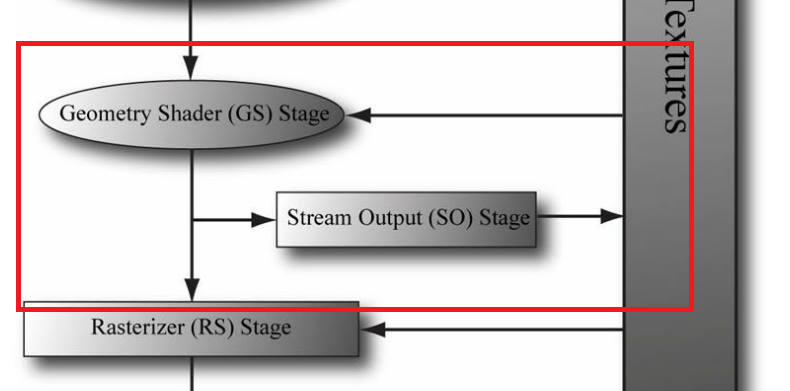
위 그림에서 볼 수 있듯, 지오메트리 쉐이더는 정점 데이터를 리소스 메모리로 스트림 아웃하며, 이 데이터를 이용하여 나중에 렌더링에 사용할 수 있다.
이는 고급 기술이며, 이후의 장에서 다룰 것이다.
다음 파이프라인은 동차 클립 공간의 좌표를 기대하고 있기 때문에,
항상 출력은 동차 클립 공간에 닫혀있어야 한다.
클리핑 Clipping
뷰 프리스텀 바깥에 완전히 있는 기하는 삭제되어야 하고, 프ㅓ스텀 경제와 교차하는 기하는 보이는 부분만 남도록 잘라내야 하는데, 이를 클리핑이라고 한다.
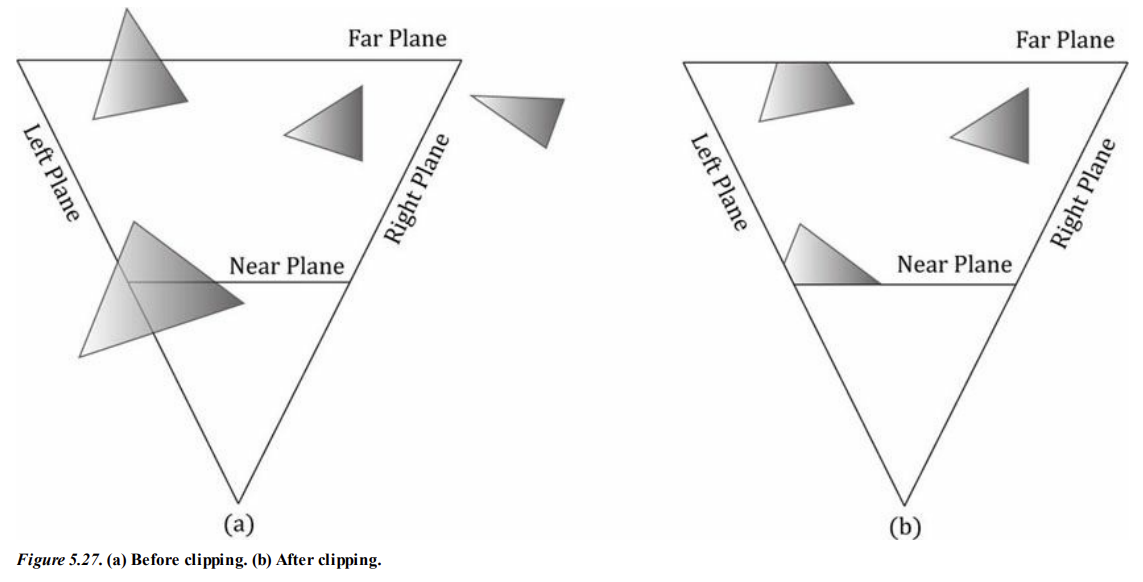
(b)가 클리핑 된 후의 프러스텀 내부이다.
보다시피 클리핑 된 후에 삼각형이 사각형으로 변할 수 있다.
따라서 하드웨어는 결과적으로 생성된 사각형에 대해 삼각형으로 변환해야 하며, 이를 triangulate 라고 한다.
이는 볼록 다각형에 대해서는 간단하게 수행할 수 있다.
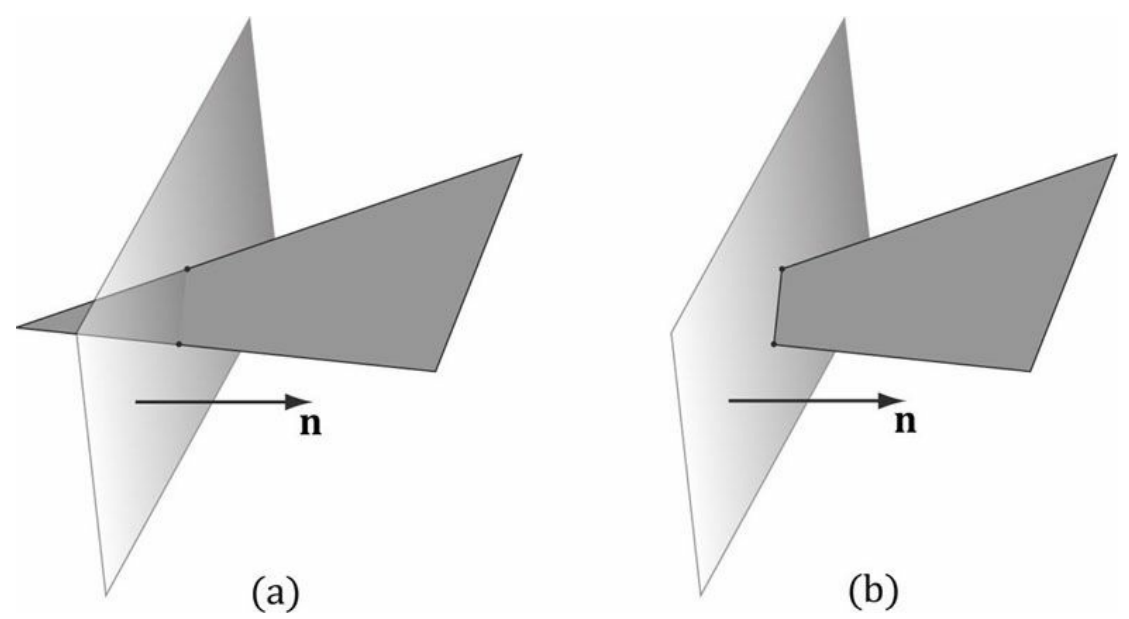
프러스텀은 6개의 평면으로 이루어져 있다.
상, 하, 좌, 우, 근, 원평면
프러스텀에 대해 폴리곤을 클리핑하기 위해서는 각 프러스텀 평면에 대해 하나씩 클리핑해야 한다.
프러스텀을 이루는 각 평면의 normal 벡터들은 프러스텀 내부를 향하고 있다.
그러므로 폴리곤을 평면에 대해 클리핑 할 때, 평면의 법선 벡터에 해당하는 부분은 유지하고, 그 반대에 있는 부분은 버리는 방식으로 진행된다.
볼록 다각형을 평면에 대해 클리핑하면 항상 볼록 다각형이 남게 된다.
하드웨어가 클리핑을 처리해주기 때문에 여기서는 세부 사항을 다루지 않고, Sutherland-Hodgeman 클리핑 알고리즘을 참고하길 바란다.
기본적으로 클리핑은 프러스텀을 이루는 평면과 폴리곤의 정점들을 잇는 선이 교차하는 지점을 찾아, 새로운 폴리곤을 형성하기 위해 버텍스 위치를 계산하는 과정이다.
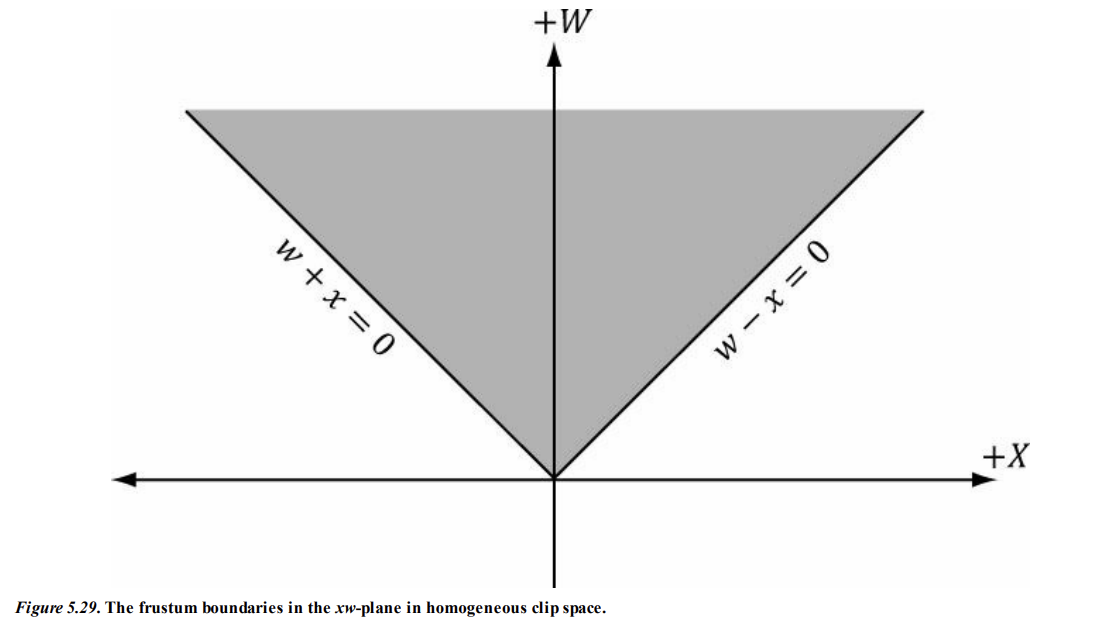
NDC 장치 좌표계에서는 다음과 같은 부등식이 성립한다.
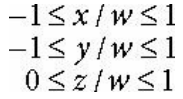
이를 동차 클립 공간까지 확장을 해보면 아래와 같다.
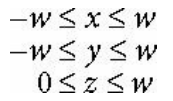
이 점들은 아래와 같은 4D 평면에 의해 제한된다.
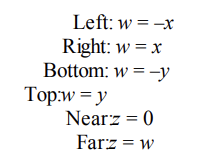
책에는 잘 나와있지 않지만..
클리핑 알고리즘은 점P1 과 점P2의 사이 직선이 절두체 평면과 만나는 정점(교차점)을 찾는 것이 목표이다.
그러허게 새로운점 P3를 찾아내면, 그 점을 기준으로 클래핑을 수행할 수 있다.
그 점을 찾아내는 방법은 컨벡스 결합식을 이용하는 것이다.
자세한 것은 해당 블로그의 '삼각형 클리핑'을 검색해서 찾아보면 된다.
클리핑은 래스터라이저 단계에 수행되는 계산 작업 중 하나로, 독립적인 쉐이더 단계와 같은 명시적인 파이프라인 단계로 구분되지는 않는다.
동차 클립 공간에서 프러스텀 평면 방정식을 알게 되면, 클리핑 알고리즘을 적용할 수 있다.
*참조
앞서 말했듯, 동차 클립 공간에서의 프러스텀 평면 방정식을 구하는 방법은 쉽다.
NDC 공간에 포함되는 좌표는 다음과 같다.
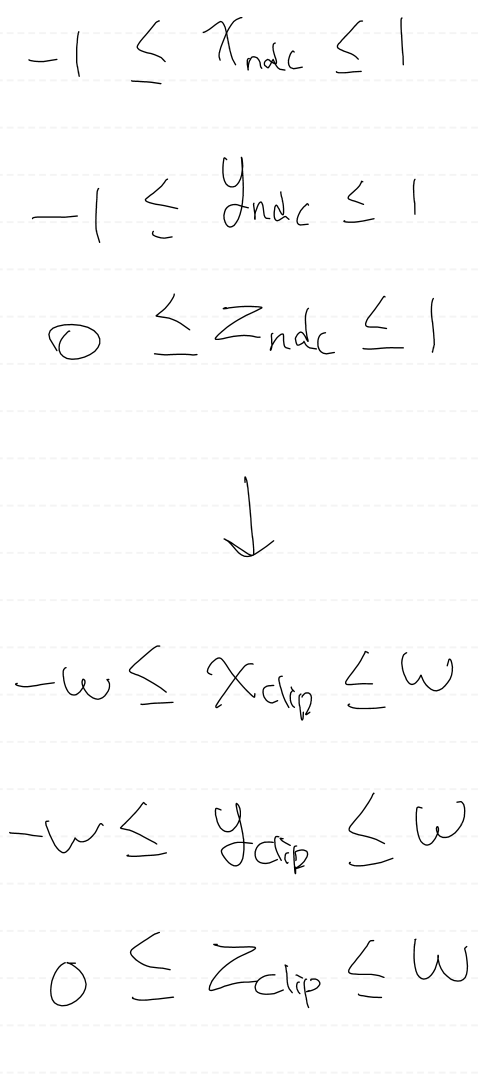
w를 곱하면 clip 좌표계를 기준으로 부등식을 바꿀 수 있다.
해당 부등식을 통해서, 6개의 평면을 정의할 수 있다.

이것이 곧 클립 공간에서의 프러스텀 평면 방정식이다.
이 수학적 원리를 이용하여 클립 공간에서의 선분과 평면 교차 테스트를 수행할 수 있고, 교차점을 손쉽게 구할 수 있다. (컨벡스 결합이든, 아핀 결합이든, Lerp든.. 사용해서 구하면 된다.)
Rasterization State (RS)
래스터화 단계의 주요 작업은 투영된 3D 삼각형들로부터 픽셀 색상을 계산하는 것이다.
1. 뷰포트 변환
클리핑 후, 하드웨어는 클린 좌표계에서 NDC 좌표계로 변환하기 위해 동차 나눗셈을 수행할 수 있다.
투영 부분에서 선형 변환과 비선형 변환을 나눈다하여, w값을 남겨놨던 것을 기억할 것이다.
드디어 이 녀석들을 없앨 수 있는 기회가 왔다.
정점이 NDC 공간에 있으면, 2D 이미지를 구성하는 x 및 y 좌표는 뷰포트라고 불리는 백 버퍼의 직사각형으로 변환된다.
NDC 공간 [-1, 1] 의 좌표들을 버퍼의 사이즈만큼 늘리는 작업이다.
이 변환 후, x, y 좌표는 픽셀 단위의 표현으로 변경된다. 이러한 좌표계를 스크린 좌표게라고 표현한다.
일반적으로 뷰포트 변환은 z 좌표는 수정하지 않는다. z 좌표는 깊이 버퍼에서 관리하기 떄문이다.
D3D11_VIEWPORT 구조체의 MinDepth와 MaxDepth 값을 수정하여 z-좌표를 변경할 수 있다.
MinDepth와 MaxDepth 의 값은 [0, 1] 의 값을 가져야 하며,
해당 설정을 이용해서 깊이를 제한하여 특정 효과를 주는데 활용할 수 있다.
2. 백 페이스 컬링
삼각형에는 후면과 전면이 존재한다.
이 두 면을 구분하기 위해 삼각형의 꼭짓점을 이용하여 삼각형의 법선 n을 다음과 같이 계산한다.
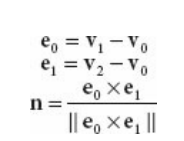
법선 벡터가 나오는 면이 앞면이고, 다른 면이 뒷면이라고 여긴다.
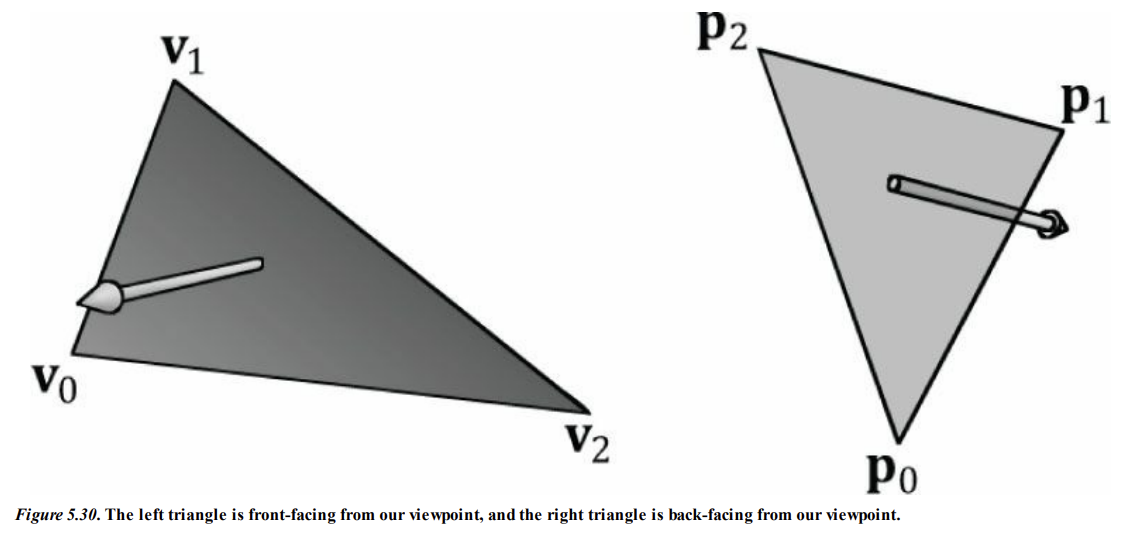
우리 시점에서 오니쪽 삼각형을 시계방향으로 정렬되어 있고, 오른쪽 삼각형은 반시계방향으로 정렬되어 있다.
이것은 우연이 아니다. 우리가 선택한 규칙에서는 시계방향으로 정렬된 삼각형이 앞면이고
반시계방향으로 정렬된 삼각형이 뒷면이다.
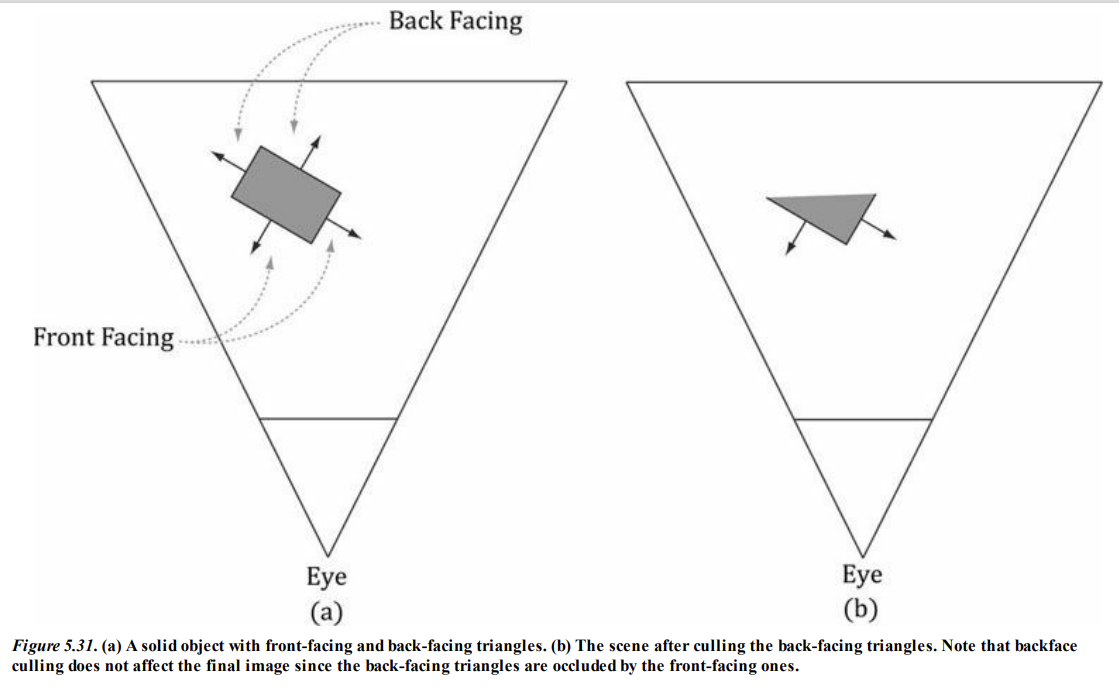
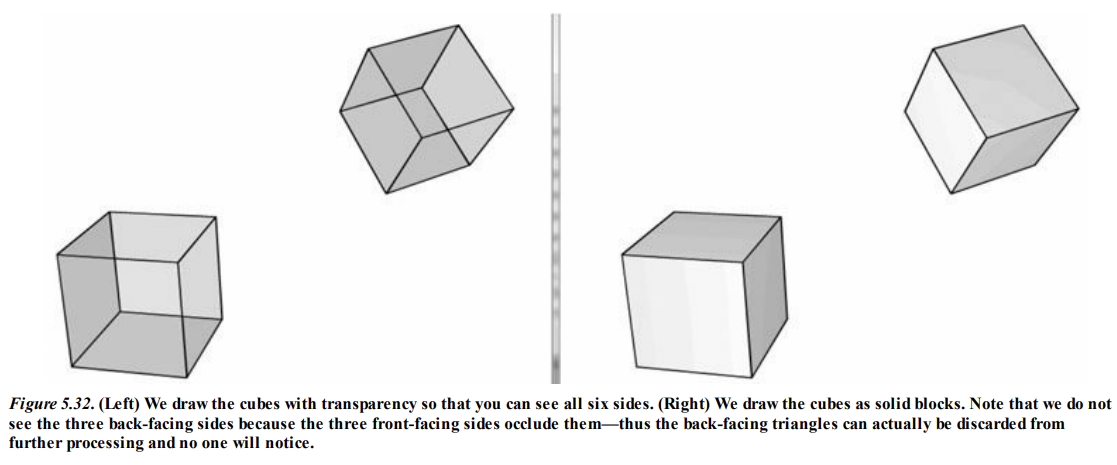
카메라는 실체 객체의 뒷면 삼각형을 보지 못한다. 이는 앞면 삼각형이 뒷면 삼각형을 가리기 때문이다.
그러므로 뒷면 삼각형을 그리는 것은 의미가 없다.
백페이스 컬링은 파이프라인에서 뒷면 삼각형을 제거하는 과정을 말한다.
이 과정에서 그려야할 삼각형의 양을 절반으로 줄일 수 있다.
기본적으로, Direct3D는 시점에 대해 시계방향으로 정렬된 삼각형을 앞면으로, 반시계방향으로 정렬된 삼각형을 뒷면으로 처리한다.
그러나 이 규칙은 Direct3D 렌더 상태 설정을 통해 반대로 변경할 수 있다.
3. Vertex Interpolation
삼각형은 버텍스들에 의해서 정의된다.
버텍스에는 위치 외에도, 색상, 법선 벡터, 텍스처 좌표 등.. 여러 속성을 부착할 수 있다.
뷰포트 변환 후, 삼각형을 덮고 있는 각 픽셀에 대해 이러한 속성들을 보간해야 한다.
버텍스 속성 외에도, 깊이 버퍼링 알고리즘을 위해 각 픽셀이 깊이 값을 가지도록 버텍스 깊이 값도 보간해야 한다.
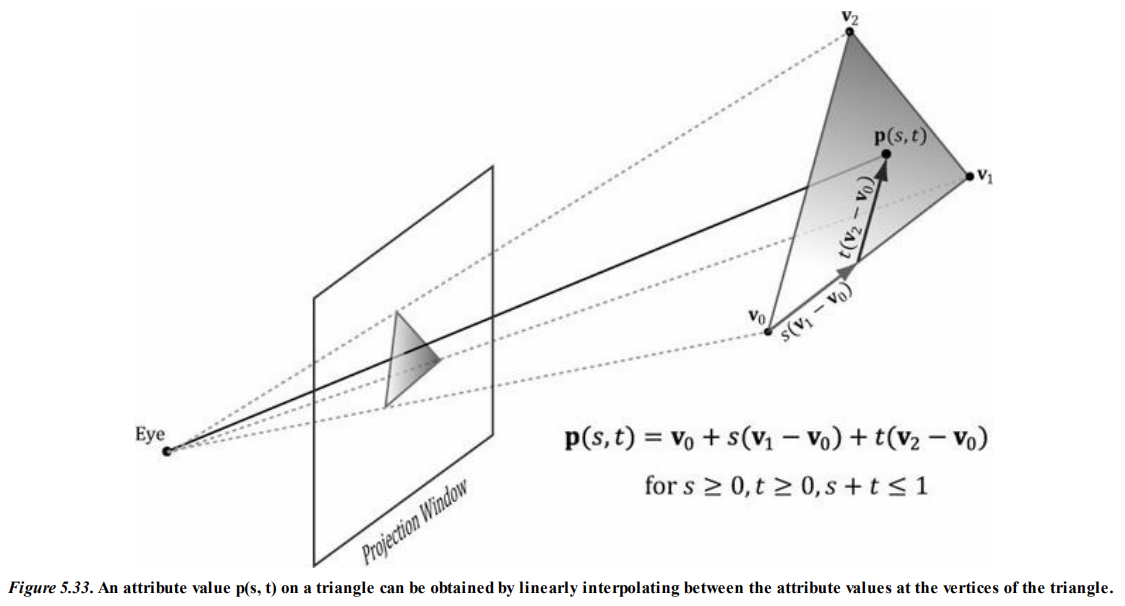
버텍스 속성들은 스크린 공간에서 보간되며, 이때 속성들이 3D 공간의 삼각형 전체에 걸쳐 선형적으로 보간되도록 한다.
그런데, 일반적인 선형 보간으로는 부족하고 원근 보정 보간이 필요하다.
본질적으로 보간은 버텍스 값을 사용하여 삼각형 내부 픽셀의 값을 계산할 수 있도록 한다.
원근 보정 보간의 수학적 세부 사항은 하드웨어가 처리하므로 우리가 걱정할 필요는없다.
(제 블로그에 찾으면 수학적 유도를 찾을 수 있습니다. ^^ 별로 안어려워요.)
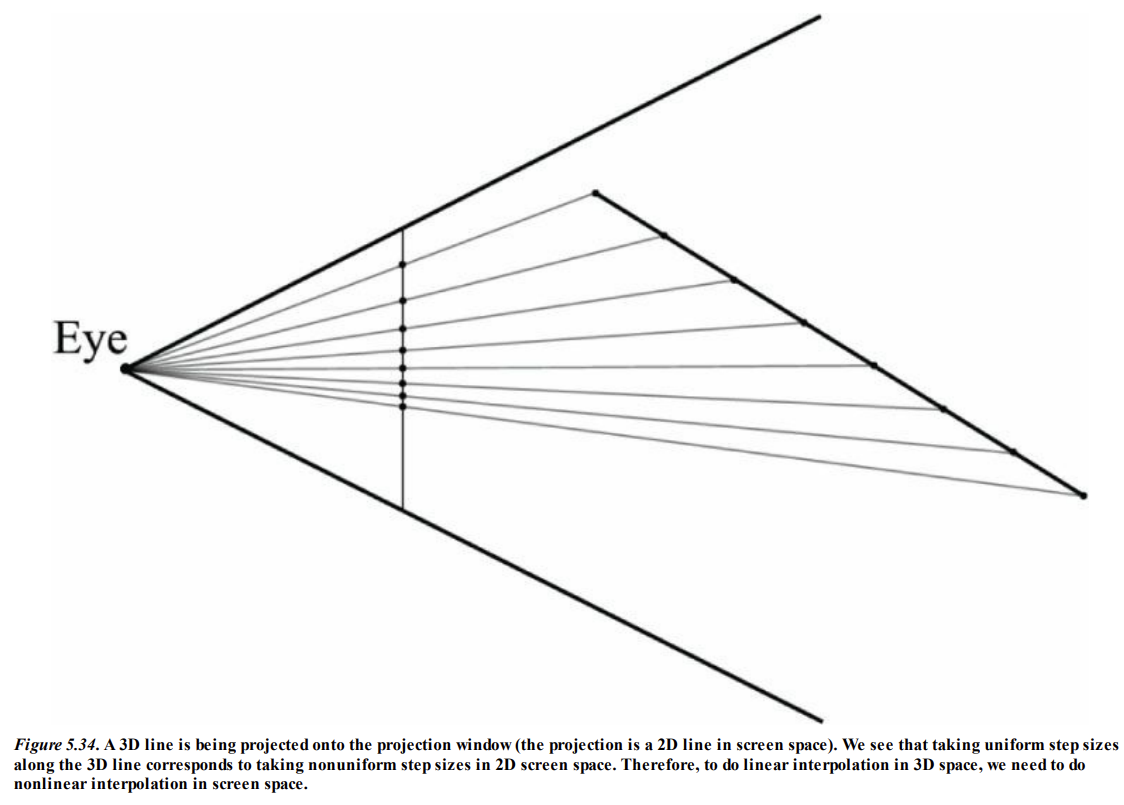
그냥 넘기기 아쉬우니까 한 번 해보겠다.
삼각형을 색칠할 때, 삼각형을 포함하는 가장 큰 사각형을 구한 뒤
사각형을 순회하며 해당 사각형 픽셀이 삼각형 내부에 있는가, 외부에 있는가를 판단하여 픽셀을 찍는다.
해당 픽셀이 삼각형 내부에 있는가? 를 확인하기 위해 세 점의 컨벡스 결합식을 이용한다.
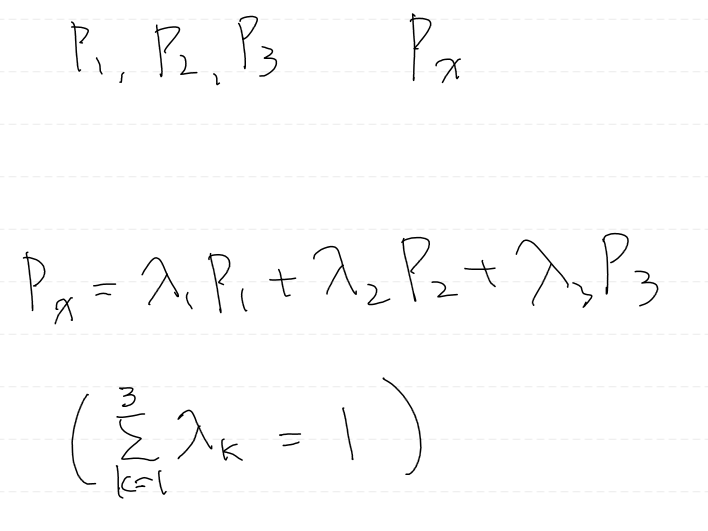
삼각형 내부에 있는 점은 위 컨벡스 결합식을 만족해야 한다.
정확히는 삼각형 외부에 있는 점은 상수를 모두 더했을 때의 값이 1이 되지 않는다.
식을 조금만더 간단하게 바꿔보겠다.
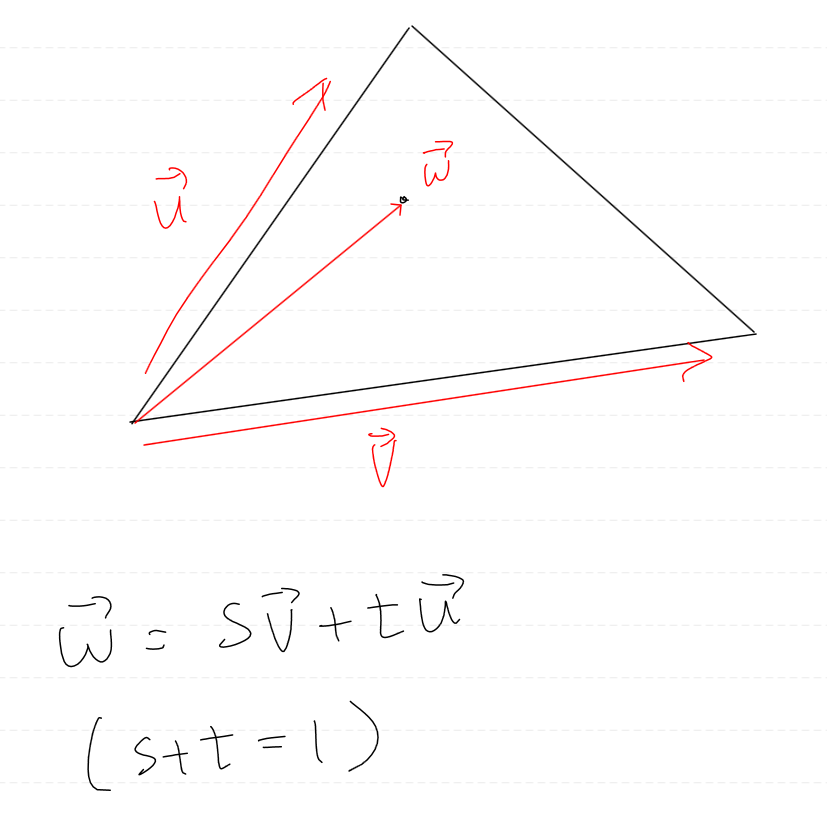
이제 s와 t를 얻어내야 하는데 이는
w와 u의 내적
w와 v의 내적을 각각 전개하면 얻을 수 있다.
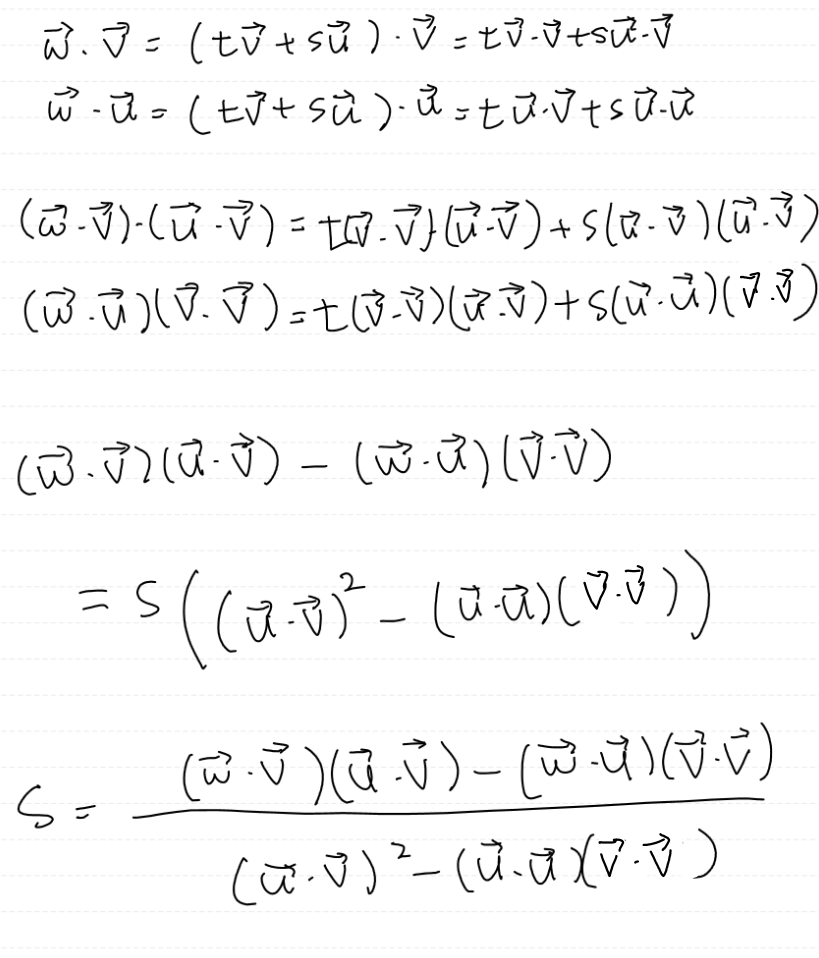
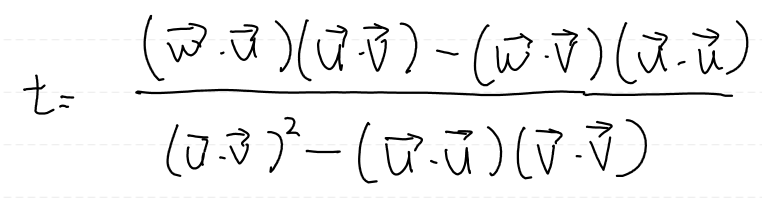
여기서 얻어낸 s, t, 그리고 마지막 계수 (1 - s - t)를 이용하면
해당 점이 삼각형 어디에 위치해 있는지 식별할 수 있다.
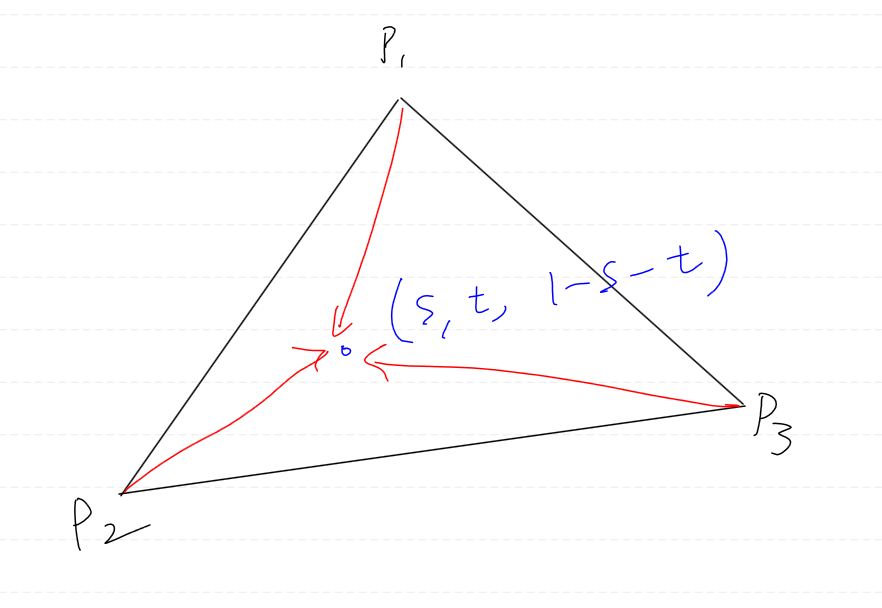
다른 방식으로 말하면
삼각형 내부에 있는 점이 각 정점 벡터에 얼마나 영향을 받았냐? 로도 해석할 수 있다.
즉, 이를 통해서 정점의 UV 좌표, 색상, 법선벡터, 깊이 등을 보간할 수 있는데
이를 무게중심보간이라고 부른다.
그런데 생각해보면, 클립 공간에서 NDC 좌표로 변환하는 과정에서, 비선형 연산이 포함되어 있었기에 스크린 좌표에서 구한 무게중심좌표는 기존 3D 공간의 정점들의 무게중심을 정확히 나타내지는 않을 것이다.
그러므로 정확한 보간을 하기 위해서는 스크린 좌표에 존재하는 정점이 아니라 뷰 공간에 존재하는 정점을 이용하여 보간하는 것이 올바를 것이다.
그러나 파이프라인을 역행할 수는 없기 때문에 상당히 곤란한 것이 현실이다.
그렇기 때문에 수학적 성질을 이용하여 뷰 공간에 있는 무게중심좌표를 구하고자 한다.
이것을 원근 투영 보간이라고 한다.
개요를 말해보면, 스크린 좌표에서 구한 무게중심좌표를 클립 공간까지 확장하는 것이 주된 아이디어이다.
어차피 클립 공간까지는 선형적으로 변환되었기 때문에 클립 공간까지만 확장해도 정확한 무게중심좌표를 구할 수 있다.
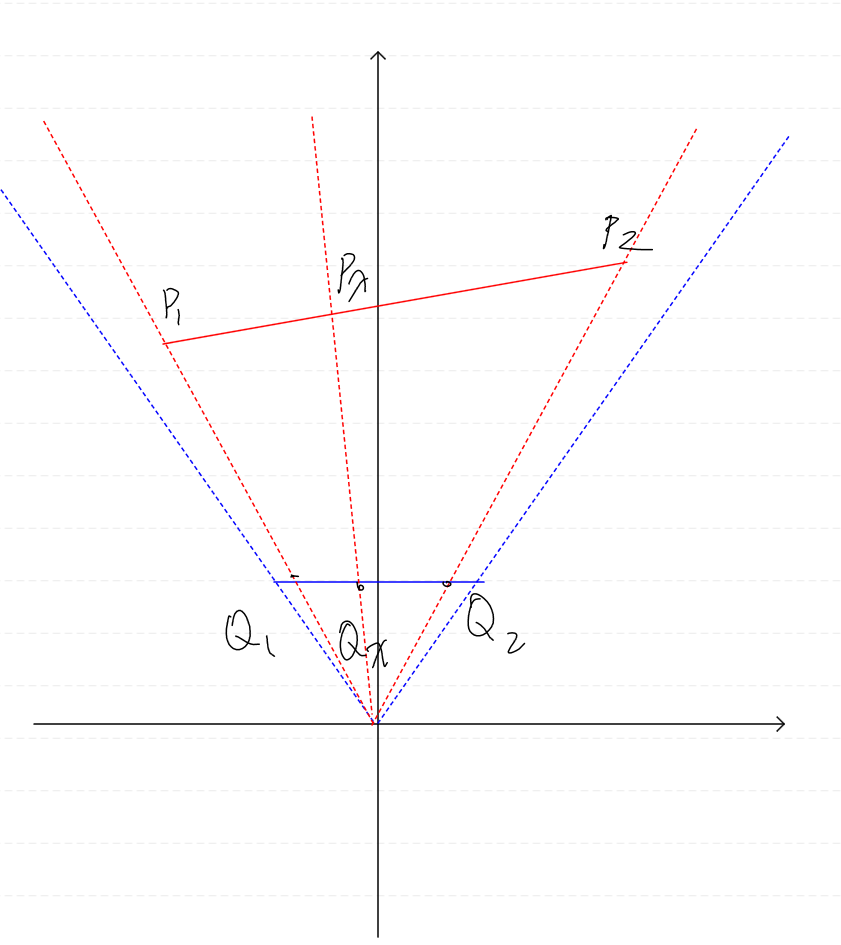
어떤 직선을 투영 평면으로 원근 투영한 예시를 보도록 하자.
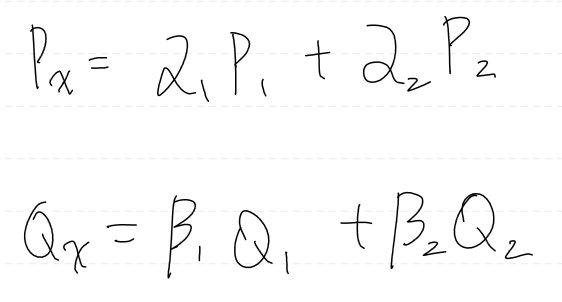
직선 사이의 어떤 점은 컨벡스 결합 식을 이용해서 간단하게 구할 수 있다.
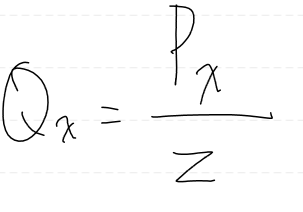
그리고 Q와 P의 관계는 위와 같다.
이제 P에 Q를 대입해보자.
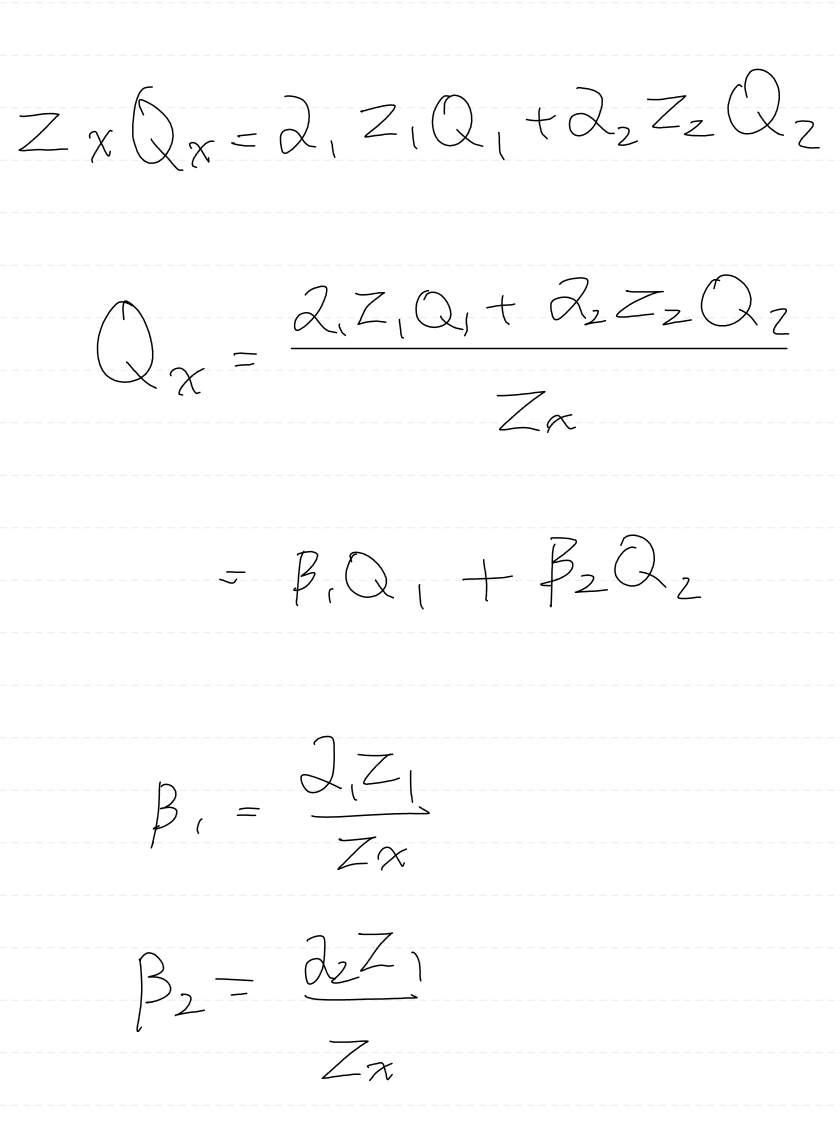
우리가 구하고자 하는 것은 알파 값이므로
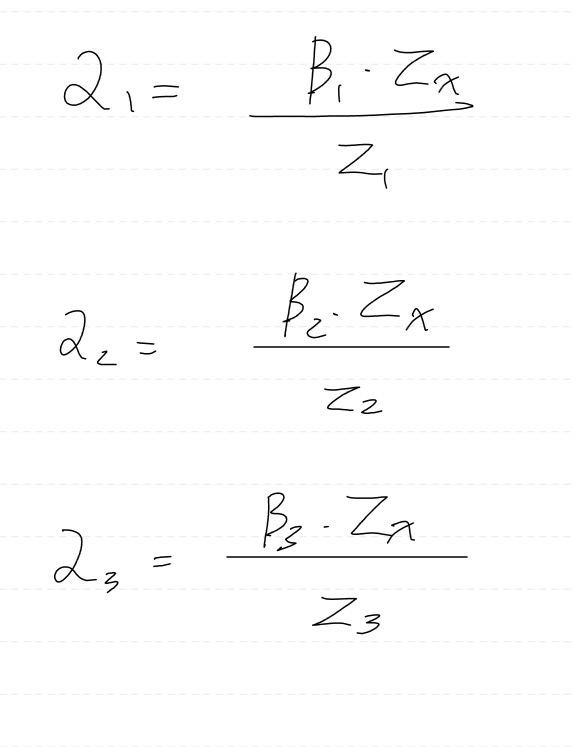
정리하면 위와 같다.
알파 인덱스가 3까지 생긴 이유는,, 계산의 단순화를 위해서 2D 로 생각하고 식을 전개했기 때문이다.
그래서 3차원으로 확장시켜주었다.
이제 zx 를 구해야 하는데, 이는 컨벡스 결합의 계수 합 특성을 이용하여 구할 수 있다.
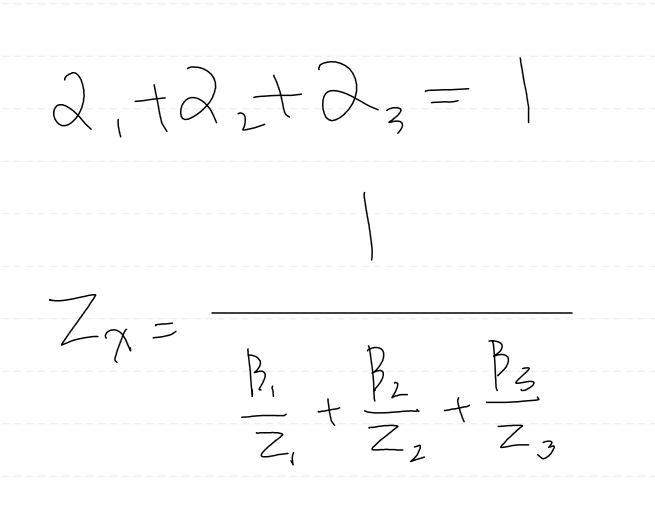
우리는 이미 스크린 좌표계의 무게중심 좌표를 알고있다.
더하여 동차 나누기는 RS 단계에서 수행하기 때문에, 기존 z1, z2, z3 도 여전히 동일한 파이프라인 단계에서 얻어낼 수 있다.
그러므로 우리는 파이프라인을 역행하지 않고 원근 투영 보간에 필요한 계수들을 모두 얻어낼 수 있다.
Pixel Shader Stage (PS)
픽셀 쉐이더는 우리가 작성한 프로그램으로 GPU에서 실행된다.
이 단계에서 각 픽셀에 대한 색상, 텍스처 효과, 조명, 반사 등의 그래픽 효과를 계산한다.
픽셀 프래그먼트는 프레임 버퍼에서 하나의 픽셀을 생성하는 데 필요한 데이터를 의미한다.
이 데이터에는 스크린 위치, 깊이, 보간된 버텍스 속성, 스텐실, 알파 등이 포함되어 있다.
간단히 픽셀 프래그먼트는 해당 스크린 좌표계 그려질 후보 픽셀의 데이터 정도로 설명할 수 있다.
픽셀 쉐이더는 각 픽셀 프래그먼트에 대해 실행되며, 보간된 버텍스 속성(정확히는 픽셀 프래그먼트)을 입력으로 받아 색상을 계산한다.
픽셀 쉐이더는 단순히 색상을 계산해서 반환하는 것부터, 복잡한 작업인 픽셀 단위의 조명 반사, 그림자 효과를 처리한다.
Output Merger Stage (OM)
픽셀 쉐이더에 의해 픽셀 프래그먼트가 확정된 후, 이들은 렌더링 파이프라인의 출력 병합(OM) 단계로 이동한다.
이 단계에서 일부 픽셀 프래그먼트는 깊어 버퍼 또는 스텐실 버퍼 테스트와 같은 이유로 거부될 수 있다.
거부되지 않은 픽셀 프래그먼트는 백 버퍼에 기록된다.
이 단계에서 블렌딩도 수행되며, 픽셀이 현재 백 버퍼에 있는 픽셀과 완전히 덮어쓰는 대신 혼합될 수 있다.
투명성 같은 일부 특수 효과는 블렌딩을 통해 구현되며, 블렌딩에 대해서는 9장에서 다룬다.
간단 요약
1. Input Assembler (IA)
정점 데이터와 인덱스 데이터를 GPU에게 전달하고
지오메트리 토폴로지를 설정
2. Vertex Shader (VS)
버텍스에 대해서 행렬 곱을 수행
최종적으로 클립 공간으로 변환
3. Tessellator (선택적)
기본적인 기하학적 형태를 더 세분화하여 더 많은 정점과 삼각형을 생성
4. Geometry Shader (선택적)
새로운 프리미티드를 생성 하는 등, GPU 리소스에 추가적인 리소스를 생성하여 등록할 수 있음
5. Resterizer Stage
클리핑을 수행, NDC 좌표계 및 스크린 좌표계로의 변환이 발생하며
원근 투영 보간을 수행하고, 정점 데이터들을 보간하여 픽셀 프래그먼트를 생성함
6. Pixel Shader (PS)
픽셀 프래그먼트에 특수한 처리를 하여, 각 픽셀에 특수한 효과를 적용시켜
최종 픽셀 프래그먼트를 확정함
7. Output Merger Stage (OM)
확정된 픽셀 프래그먼트 데이터를 이용하여 백 버퍼에 픽셀을 그려냄
깊이 버퍼, 스텐실 버퍼 테스트가 이 단계에서 수행되고 블렌딩과 같은 추가적인 처리도 수행됨
'컴퓨터 그래픽스 > DirectX 11' 카테고리의 다른 글
| [물방울책 공부록] Chapter 9 Blending (2) | 2024.10.05 |
|---|---|
| [DX11 물방울책 공부록] Chapter 8: Texturing (5) | 2024.10.05 |
| [DX11 물방울책 요약 정리] 챕터4: Direct3D 초기화 (0) | 2024.09.08 |
| [DX11 물방울책 요약 정리] 챕터3: Transformations (1) | 2024.09.07 |
| [DX11 물방울책 요약 정리] 챕터2: 행렬 대수 (0) | 2024.09.07 |