개발하는 리프터 꽃게맨입니다.
[그래픽스] 2D 카메라 설계 본문
2D 카메라 설계
앞서 만든 2D 랜더링 엔진에 카메라를 추가해보겠습니다.
카메라는 화면을 만들어내는 기준이 됩니다.

이런 식으로 무한한 크기의 월드가 존재하고
카메라가 비추는 방향 바꾸거나, 카메라를 회전시키거나, 카메라를 줌인 줌아웃 시켜서 세상을 입체적으로 표현할 수 있습니다.
카메라 또한 3가지 변환을 수행합니다.
1. 이동 변환
2. 회전 변환
3. 크기 변환
해당 선형 변환으로 만들어낸 행렬을 카메라의 모델링 행렬이라고 합니다.
그러면 이 카메라의 모델링 행렬을 이용해서 윈도우에 렌더링 하는 방법을 설명합니다.
설명을 간단하게 하기 위해서 이동 변환만 수행한다치고 설명해보겠습니다.

이런 식으로 월드와 많은 종류의 오브젝트, 3사분면에 위치하는 카메라가 존재한다고 해봅시다.
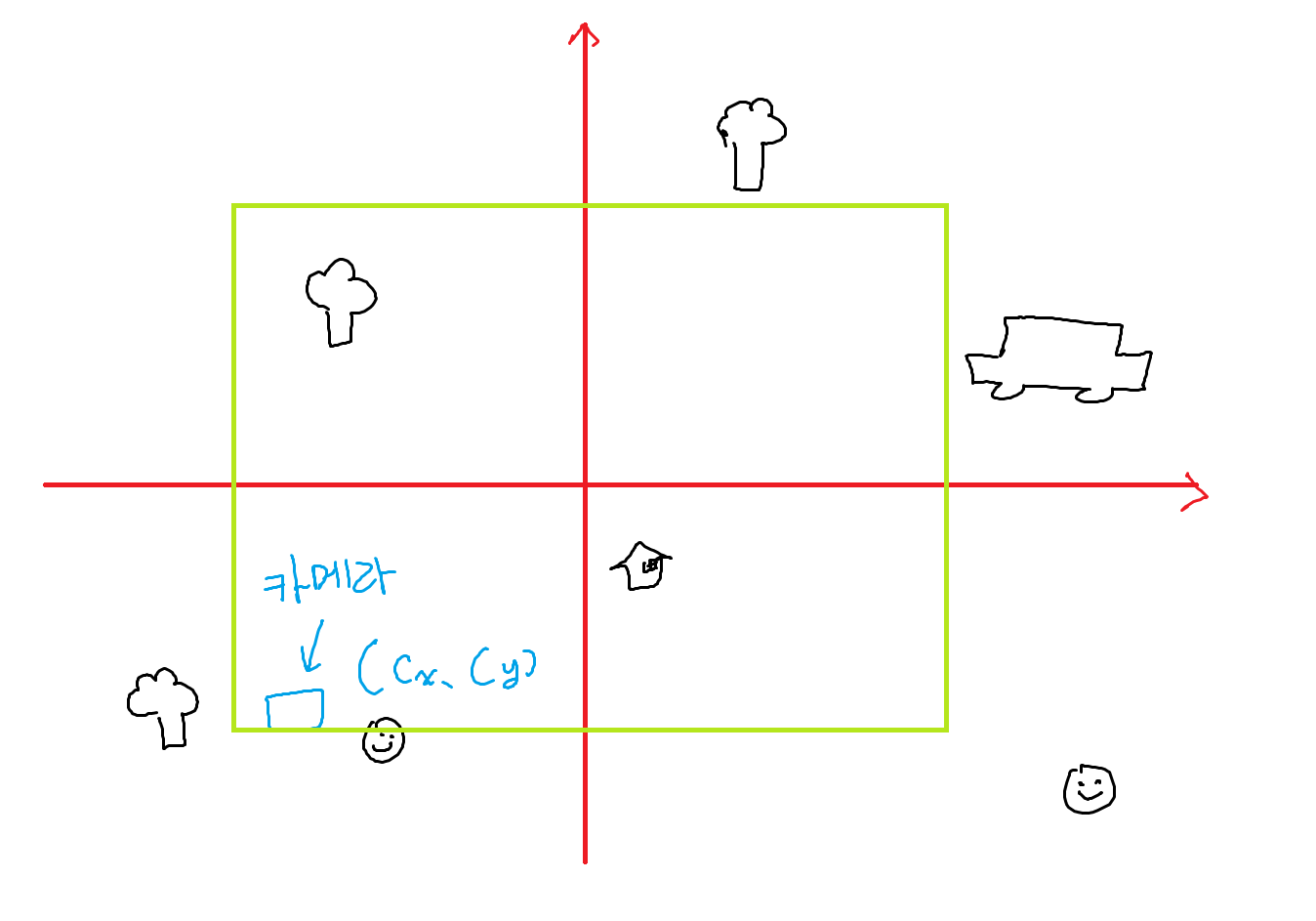
실질적으로 윈도우에 그려지는 화면을 저기 초록색 사각형 만큼입니다.
하지만 우리는 카메라의 위치를 기준으로 랜더링을 해야합니다.
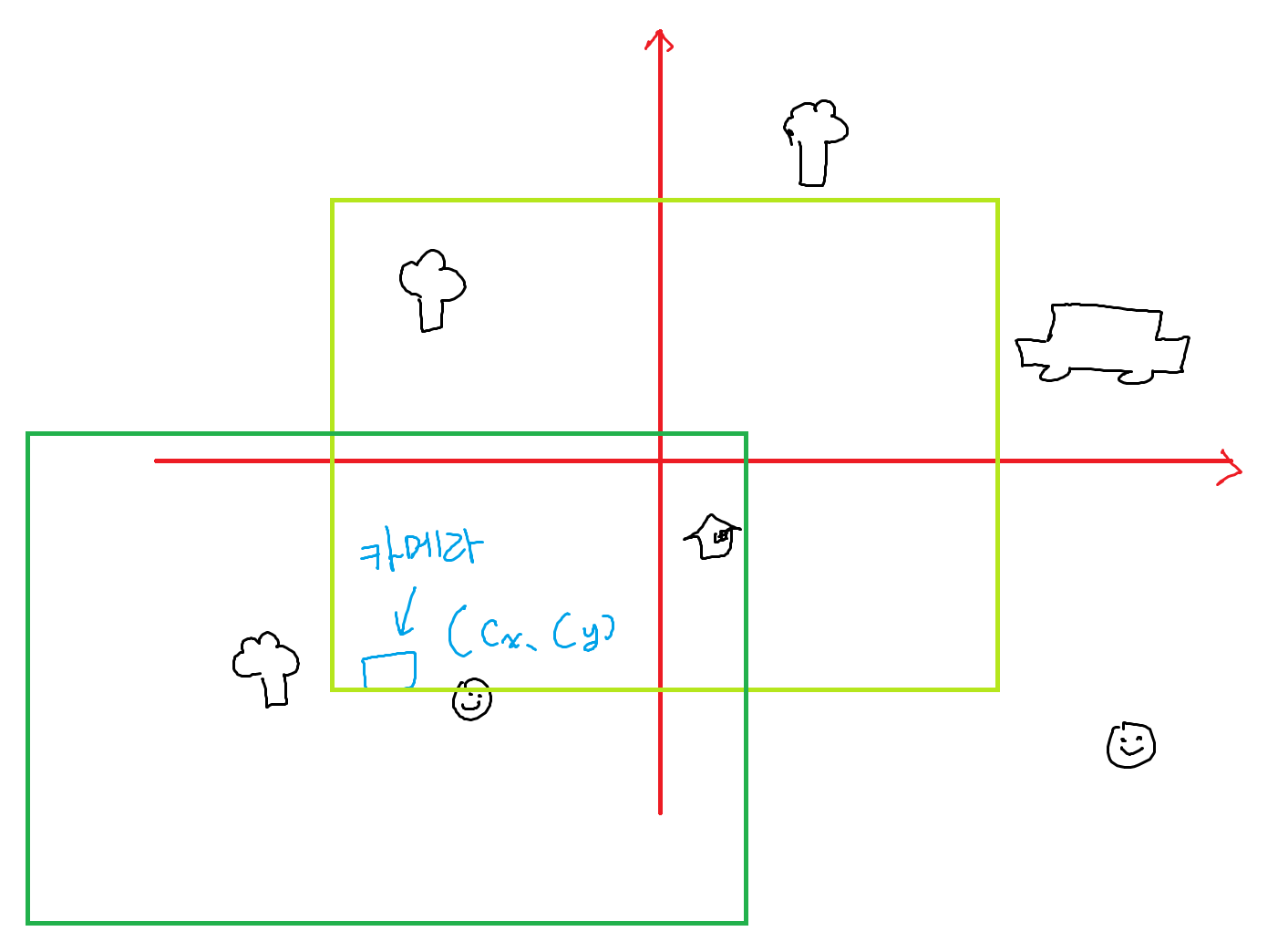
이만큼 말이죠
진한 초록색 사각형을 카메라 뷰라고 하겠습니다.
카메라 뷰를 윈도우와 맞춰주기 위해서는 모든 오브젝트의 위치를
(-Cx, -Cy) 만큼 이동해주어야 합니다.
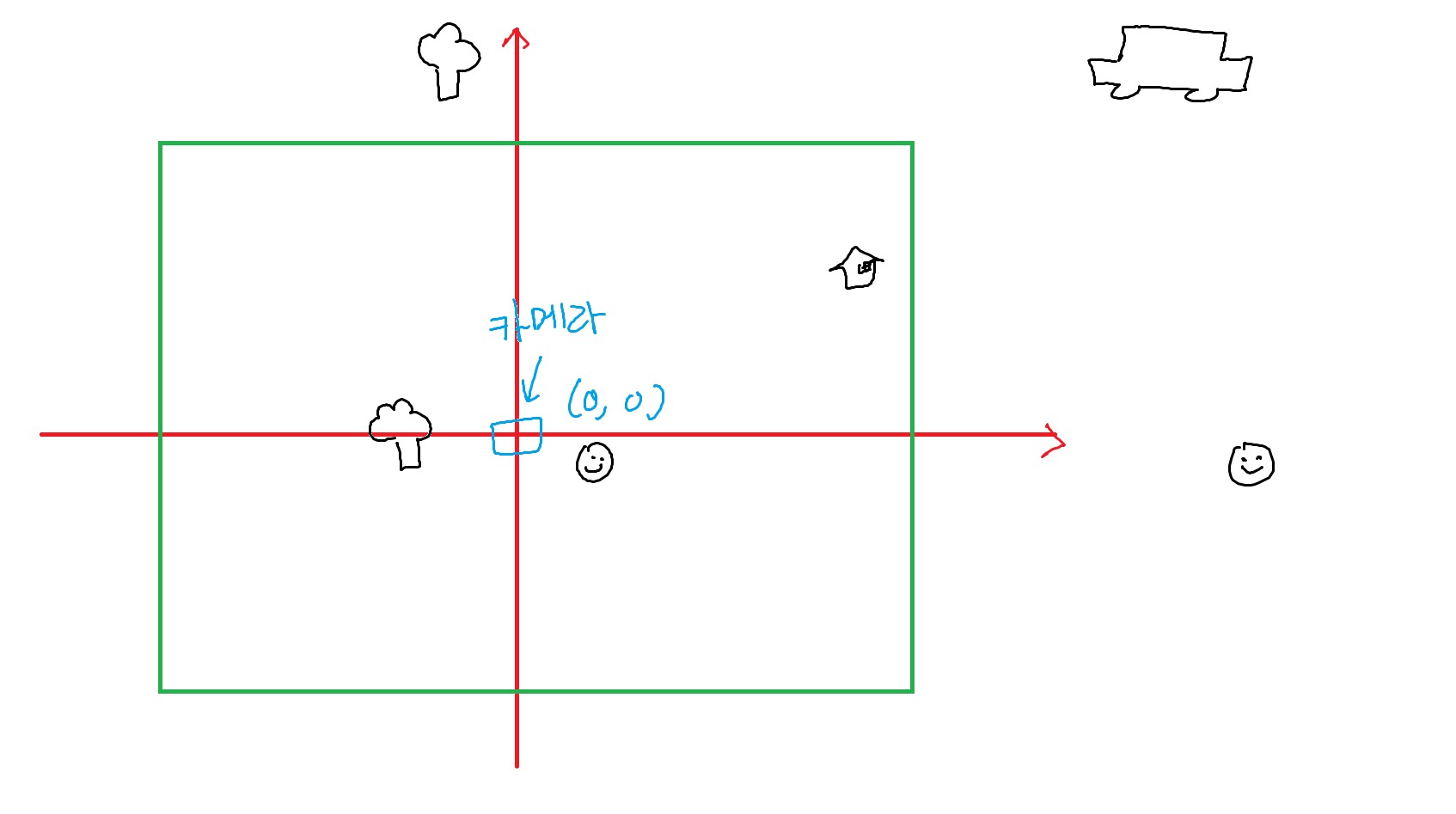
이렇게 말이죠.
이렇게 카메라 뷰와 윈도우의 위치를 맞춰주면 딱 카메라가 비추는 장면만을 그릴 수 있게 됩니다.
뷰 행렬 설계
즉, 카메라를 원점으로 돌려야 합니다.
여기서 회전, 크기 변환 관점을 더하면
카메라의 위치는 원점
회전각은 0도
크기는 1배
만큼으로 되돌려야 합니다.
즉, 카메라의 모델링 행렬의 역행렬을 구해야 한다는 것이죠?
계산해봅시다.
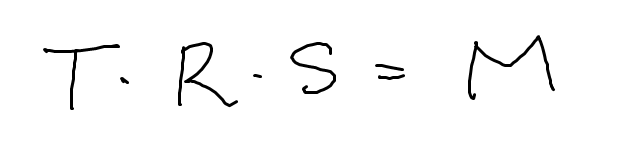
모델링 행렬은 위와 같습니다.
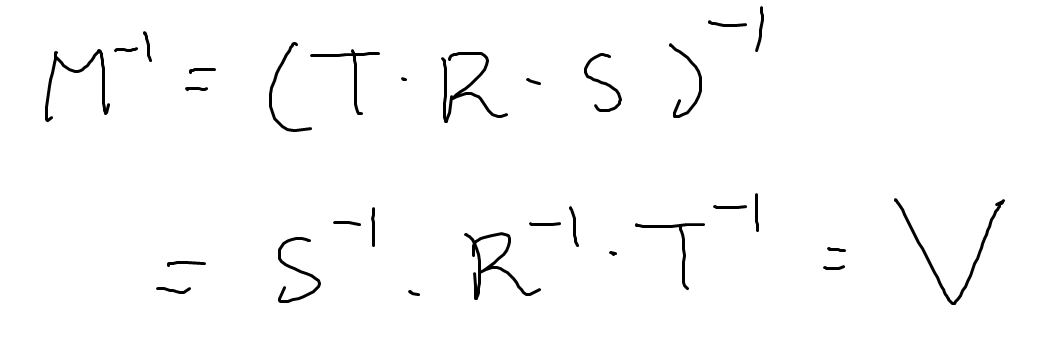
카메라의 모델링 행렬의 역행렬을 뷰 행렬이라고 합니다.
우리의 목표는 해당 뷰 행렬을 구하는 것입니다.
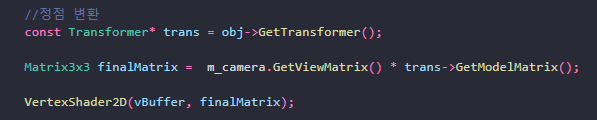
이런 식으로 최종 정점에 모델링 행렬을 곱하고, 뷰 행렬을 추가로 곱해주면, 모든 정점이 카메라 변환의 역만큼 변환됩니다.
즉, 카메라 뷰와 윈도우의 위치, 크기, 각도를 맞춰주기 위해서 모든 월드 오브젝트들이 변환된다는 의미입니다.
처음에는 이해가 조금 어려울 수 있습니다.
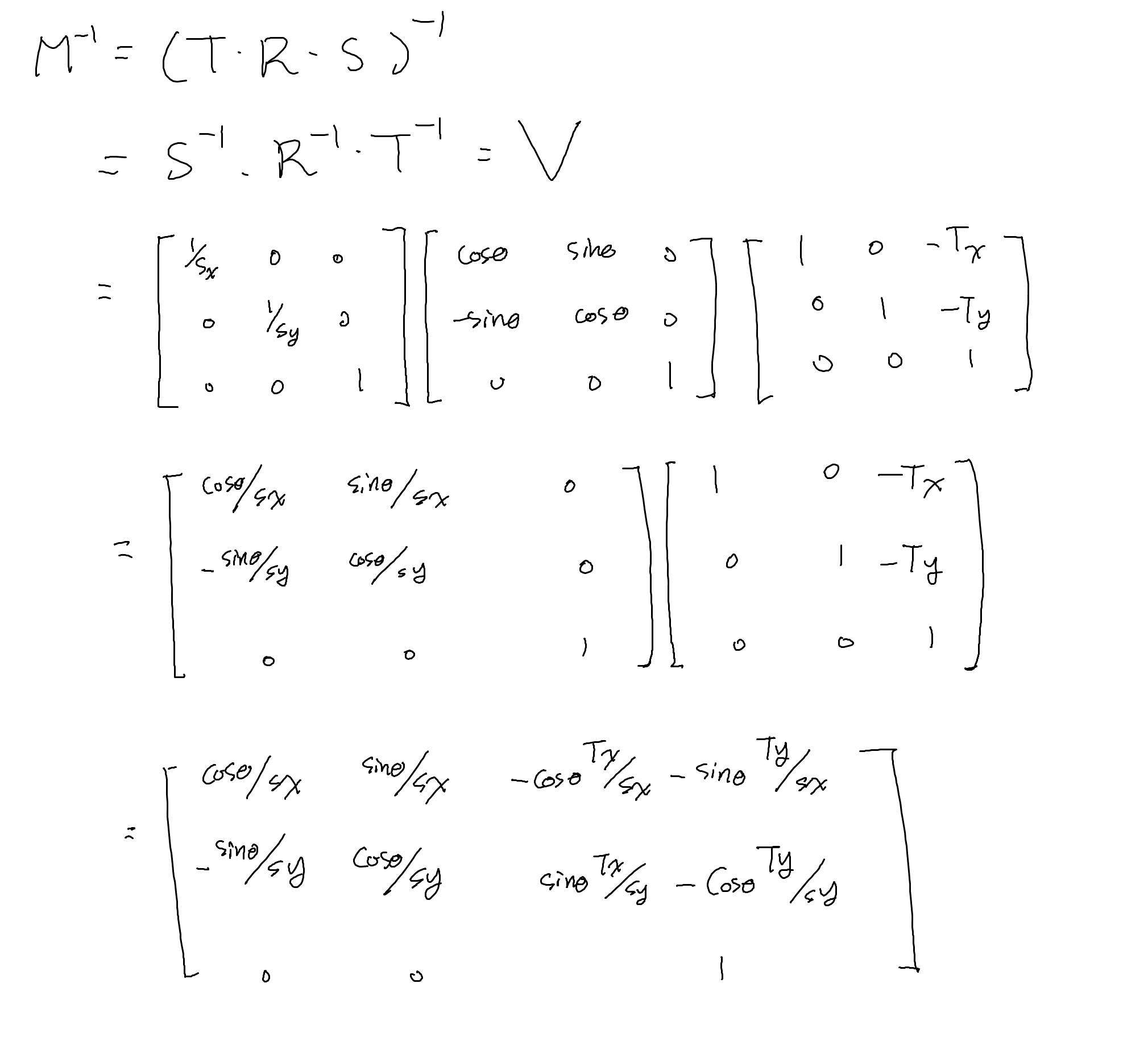
최종 뷰 행렬을 미리 계산합니다.
카메라의 코드는 다음과 같습니다.
#pragma once
class Camera2D
{
public:
Camera2D() = default;
virtual ~Camera2D() = default;
inline void AddPosition(const Vector2D& _vector);
inline void SetPosition(const Vector2D& _vector);
inline Vector2D GetPosition() const;
inline void AddRotation(float _degree);
inline void SetRotation(float _degree);
inline float GetRotation() const;
inline void AddZoom(float ratio);
inline void SetZoom(float ratio);
inline float GetZoomRatio() const;
inline Matrix3x3 GetViewMatrix() const;
inline Vector2D GetLocalBasisRight() const;
inline Vector2D GetLocalBasisUp() const;
inline Vector2D GetUnitVector() const;
private:
inline void UpdateLocalBasis();
private:
Vector2D m_position = Vector2D::s_zeroVector;
float m_degreeRotation = 0.f;
float m_zoomRatio = 1.f;
Vector2D m_localBasisRight = Vector2D::s_basisVectorX;
Vector2D m_localBasisUp = Vector2D::s_basisVectorY;
};
inline void Camera2D::AddPosition(const Vector2D& _vector)
{
m_position = m_position + _vector;
}
inline void Camera2D::SetPosition(const Vector2D& _vector)
{
m_position = _vector;
}
inline Vector2D Camera2D::GetPosition() const
{
return m_position;
}
inline void Camera2D::AddRotation(float _degree)
{
m_degreeRotation += _degree;
UpdateLocalBasis();
}
inline void Camera2D::SetRotation(float _degree)
{
m_degreeRotation = _degree;
UpdateLocalBasis();
}
inline float Camera2D::GetRotation() const
{
return m_degreeRotation;
}
inline void Camera2D::AddZoom(float ratio)
{
m_zoomRatio += ratio;
}
inline void Camera2D::SetZoom(float ratio)
{
m_zoomRatio = ratio;
}
inline float Camera2D::GetZoomRatio() const
{
return m_zoomRatio;
}
Matrix3x3 Camera2D::GetViewMatrix() const {
float tx = -m_position.X;
float ty = -m_position.Y;
float sx = m_zoomRatio;
float sy = m_zoomRatio;
float cosV = m_localBasisRight.X;
float sinV = m_localBasisRight.Y;
return Matrix3x3{
{ cosV * sx, sinV * sy, cosV * tx * sx - sinV * ty * sy },
{ -sinV * sx, cosV * sy, sinV * tx * sx + cosV * ty * sy },
{ 0.f, 0.f, 1.f }
};
}
inline Vector2D Camera2D::GetLocalBasisRight() const
{
return m_localBasisRight;
}
inline Vector2D Camera2D::GetLocalBasisUp() const
{
return m_localBasisUp;
}
inline Vector2D Camera2D::GetUnitVector() const
{
return m_localBasisRight;
}
inline void Camera2D::UpdateLocalBasis()
{
MM::Circular(m_degreeRotation, -180.f, 180.f);
float sinV = 0.f;
float cosV = 0.f;
MM::GetSinCos(sinV, cosV, m_degreeRotation);
m_localBasisRight = Vector2D(cosV, sinV);
m_localBasisUp = Vector2D(-sinV, cosV);
}
크기, 회전, 이동 변환의 역행렬은 매우 구하기 쉽습니다.
크기 변환의 역행렬은 곱셈의 역원
이동 변환의 역행렬은 덧셈의 역원
회전 변환의 역행렬은 전치 행렬입니다.
크기 변환은 좀 더 직관적으로 zoom 이라고 표현했습니다.
zoom으로 바꾸었기에 조금 더 직관적이게 뷰 행렬을 재구성했습니다.
zoom은 커질수록 보통 피사체가 확대됩니다.
그런데 카메라의 zoom 의 값이 커질 때, zoom의 역수를 곱해주면 피사체가 작아지기에,
zoom의 값이 커지면, 피사체가 커지도록 변경했습니다.
실습
'컴퓨터 그래픽스' 카테고리의 다른 글
| 그래픽스 공부 일지 - 삼각형, 텍스처 매핑 (0) | 2024.08.10 |
|---|---|
| 색칠된 삼각형 그리기 (0) | 2024.08.09 |
| [그래픽스] 색상보간, 모델링행렬 실습 (0) | 2024.08.07 |
| [그래픽스] 모델링 행렬 설계 (0) | 2024.08.06 |
| [그래픽스] 선 그리기 (브레젠험 알고리즘, 코헨-서더랜드 클리핑 알고리즘) (0) | 2024.08.06 |



