1. 뉴턴의 운동법칙
1687년 즈음 아이작 뉴턴은 역학에 대한 자신의 생각을 운동법칙으로 정의하여 <자연철학의 수학적 원리>라는 책을 집필하였고, '뉴턴의 운동법칙'은 해당 저서에 기록된 운동법칙이다.
이는 모든 역학의 기본인 고전역학 중에서도 제일 기본적인 법칙이자 공리이기 때문에, 매우 중요하다.
[1] 배경지식
(1) 질량 (Mass)
물체가 가진 물질의 양을 나타내며, 고전역학에서는 질량이 불변한다고 가정한다.
(2) 힘 (Force)
힘은 물체의 운동 상태를 변화시키는 요인이다.
운동 상태의 변화란 속도의 변화, 즉 가속도를 의미한다.
따라서 힘은 물체를 가속시키는 원인으로도 이해할 수 있다.
(3) 관성 (Inertia)
관성은 물체가 외부의 힘이 없을 때, 자신의 운동 상태를 유지하려는 성질이다.
더 엄밀하게 '물체가 받는 외부 힘의 총합이 0일 때, 같은 운동 상태를 유지하려는 그 물체의 경향' 이라고 정의할 수 있다.
즉
예를 들어 정지해있던 물체 가해지는 힘이 없으면 계속 정지한 상태일 것이며,
등속운동을하는 물체에 가해지는 힘이 없어 계속 등속운동하는 것도 관성이다.
따라서 관성은 정지보다 확장된 개념이라고 볼 수 있다.
(4) 가속도 (Acceleration)
가속도는 시간에 따른 속도의 변화량을 의미한다.
속도의 변화량을 걸린 시간으로 나눈 것이 평균 가속도이며, 여기서 시간의 극한으로 보낸 것이 순간 가속도이다.
흔히 말하는 것은 순간 가속도를 의미한다.
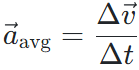

이 식에서 가속도는 속도의 시간에 대한 미분값으로 이해할 수 있다.
측정 대상의 위치가 변화한 양을 '변위'라고 말하는데
속도는 '변위 변화량 / 시간 변화량'을 의미한다.
그러므로
변위 -- (미분) --> 속도
속도 -- (마분) --> 가속도
의 관계를 보인다.
즉, 가속도는 변위를 시간으로 이계미분한 물리량이라는 것이다.

물리량 위에 있는 점 도트는 그 물리량을 시간으로 미분했다는 것을 의미한다.
위 그림은 차례로 변위, 속도, 가속도를 의미한다.
[2] 뉴턴의 운동법칙
(1) 제 1운동법칙: 관성의 법칙
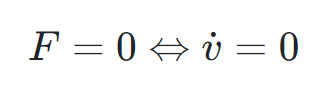
물체의 질량 중심은 외부 힘이 작용하지 않는 한 일정한 속도로 움직이다.
즉, 물체에 가해진 알짜힘이 0일 때 물체의 질량 중심의 가속도는 0이다.
참고
알짜힘(합력) 은 물체에 작용하는 모든 힘의 벡터합을 의미한다.
알짜힘은 실제 물체에 작용되는 힘이며 크기와 방향을 가지는 벡터 값이다.
(2) 제 2운동법칙: 가속도의 법칙
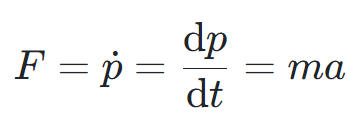
물체의 운동량의 시간에 따른 변화율은 그 물체에 작용하는 힘과 같다.
F: 합력
m: 질량
a: 가속도
p: 운동량 (선 운동량과 혼용되어 사용된다.)
이 방정식을 물체의 운동 방정식이라고 하며, 이 방정식을 풀면 물체의 운동을 구할 수 있다.
볼드체의 정의에 의하면 F = dp / dt 이다.
'선 운동량'은 p = mv (m: 질량, v: 속도) 로 정의된다.
그러므로
F = (dp / dt) = m (dv / dt) = ma
라는 공식을 얻어낼 수 있다.
그래서 일반적으로 많이 사용되는 운동 방정식은
F = ma
이다.
이 공식은 질량이 불변한다는 전제가 있어야만 성립된다.
물체의 질량이 변할 수 있다면 변형된 식을 사용해야 한다.
(3) 제 3운동법칙: 작용과 반작용의 법칙

모든 작용에 대해 크기는 같고 방향은 반대인 반작용이 존재한다.
이 법칙은 "힘은 오로지 계(System)의 외부에서만 오며 물체가 물체 스스로에 힘을 줄 수 없다." 를 의미한다.
대표적으로 총이나 대포를 발사할 시 반동을 예시로 들 수 있다.
[3] 단위와 측정
올바른 측정단위를 사용하는 것은 매우 중요하다.
속도의 단위를 '노트'로 하냐 '초속'으로 하냐는 꽤나 큰 오차를 만들어 낼 수 있다.
측정단위의 일관성을 확일할 때는 올바른 측정단위 자체를 썼는지를 확인하는 것도 중요하지만
그 측정단위를 구성하는 기본단위도 정확한지 확인해야 한다.
기본단위라 하면 질량, 길이, 시간을 의미하는데 물리량을 측정할 때는 이들을 조합해서 만든 유도단위를 흔히 사용한다.
따라서 유도단위뿐만 아니라 기본단위들의 일관성까지도 유지해야 올바른 계산 결과를 얻을 수 있다.
예를 들어, 물체의 무게는 힘의 단위로 측정하는데, 이 단위는 다음과 같은 기본 단위로 이루어져 있다.
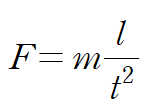
F: 힘
m: 질량
l: 길이
t: 시간
이는 앞서 살펴봤던 가속도의 법칙 F = ma 와 동일한 수식이다.
여기서 가속도 a는 유도단위이므로 기본단위로 바꾸어 도출한 것이 위 식이다.
이는 측정단위의 일관성을 검증하는 예시를 보여준다.
즉, 물체에 작용하는 힘을 나타내는 공식을 만들때는 언제나 m(l/t^2)과 같은 기본단위로 공식을 구성해야 한다.
국체단위계(SI 단위)를 사용해 물리량을 표현하기도 하는데,
다양한 단위계들이 있지만 가상 세계를 만듦에 있어 어떤 단위계를 사용해도 큰 문제는 없다.
그러나 각 단위들의 일관성은 반드시 유지해야 한다.
(일반적으로 SI 단위계를 사용한다.)
그럼, 한 번 더 확인해보자
아래 공식은 유체 속에서 움직이는 물체들의 마찰저항(항력식)을 계산한다.

이제 이 공식의 변수들을 기본단위로 바꿔보자
먼저, 좌변의 마찰저항은 '힘'이므로 이것의 측정단위는 다음과 같은 형태를 가진다.
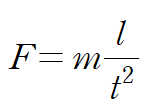
우측의 모든 항들을 합치면 그 기본단위가 이 수식과 같은 형태여야 한다.
그러면 먼저 밀도, 속도, 표면적의 기본단위를 살펴보자.

이제 이 기본단위들을 모두 합쳐보자.
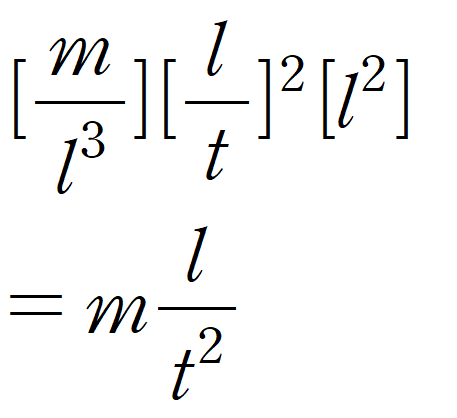
이는 앞서 봤던 마찰저항의 기본단위와 동일하다.
이걸 통해 이 공식에서 사용하는 단위들의 일관성을 확인할 수 있다.
여기서 저항계수 Cd는 반드시 무단위여야 한다.
무단위는 기본단위를 사용하지 않고 나타내어진 상태를 의미한다.
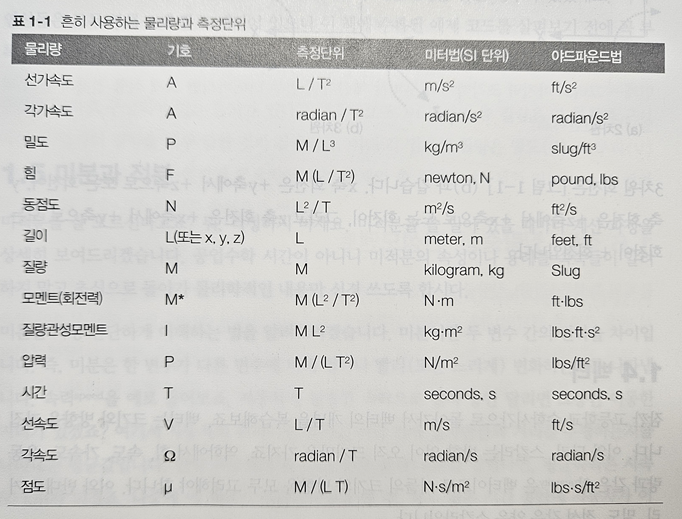
다음표는 흔히 사용하는 물리량의 열거이다.
[4] 좌표계
공간상의 위치를 표기할 떄 사용하는 일반적인 표준은 오른손 직교좌표계이다.
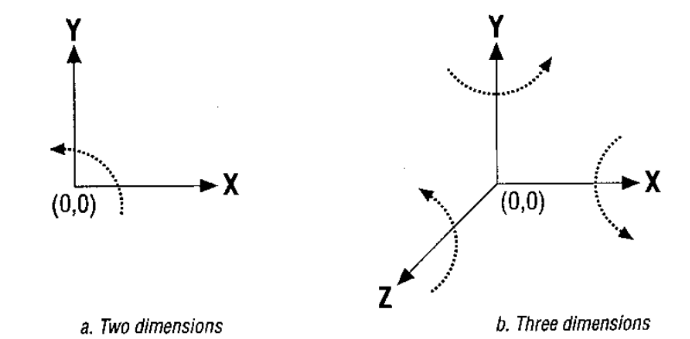
반시계 방향으로 하는 회전이 +회전이다.
3차원 회전은 그림 b와 같다. 축을 기준으로 반시계 방향으로 회전하는 것을 + 회전으로 한다.
이 좌표계는 이후에 다룰 가상 공간을 표현하기 위한 기준으로 사용될 것이다.
[5] 벡터
벡터는 크기와 방향을 가진다.
이와 달리, 스칼라는 방향 없이 오직 크기만을 가진다.
(이는 고등학교 교육과정 차원에서 정의하는 벡터이다.)
역학에서 힘, 속도, 가속도, 운동량과 같은 양은 벡터이므로 이들의 크기와 방향을 모두 고려해야 한다.
이와 반대로 거리, 밀도, 점성 같은 양은 스킬라이다.
벡터의 자세한 내용은 아래 포스팅을 참고
https://powerclabman.tistory.com/111
[수학] 벡터: 가상 공간의 탄생
이전글https://powerclabman.tistory.com/110 [수학] 수: 가상 세계를 구성하는 가장 작은 단위1. 수와 집합가상 세계를 이해하기 위한 첫걸음은 집합이라는 개념으로 수를 이해하는 것이다.중고등학교 수
powerclabman.tistory.com
[6] 미분과 적분
(1) 미분
미분이란 두 변수 간의 변화율 차이이다.
즉, 미분은 한 변수가 다른 변수에 비해 얼마나 빠르게 혹은 느리게 변화하는지를 나타낸다.
예를 들어, '속력'이란 개념을 살펴보자.
자동차가 일정한 속력으로 얼마 동안 달리면 그동안 이동한 거리가 있을 것이다.
자동차가 일정한 속력으로 이동한다고 가정하면, 일정 시간 동안 이동한 거리를 통해 평균 속력을 계산할 수 있다.
예를 들어, 자동차가 한 시간 동안 60 km를 달렸다면, 평균 속력은 시속 60 km이다.
하지만, 자동차가 달리는 동안 속력이 일정하지 않고 변할 수 있다.
이러한 변화를 이해하기 위해서는 순간 속력을 고려해야 한다.
이는 매우 짧은 시간 동안에 자동차가 이동한 거리를 고려해서 다음과 같은 수식으로 표현할 수 있다.

v는 속력
ds는 한 없이 짧은 거리 (변위)
dt는 한 없이 짧은 시간
을 의미한다.
이 수식은 한 순간에서의 속력의 변화율을 나타낸다.
수학적으로 미분은 함수 f(x)의 특정 점에서의 순간 변화율을 나타낸다.
즉, x가 아주 작은 양 h만큼 변화할 때 함수 f(x)가 얼마나 변화하는지를 나타낸다.
이를 수식으로 표현하면 다음과 같다.
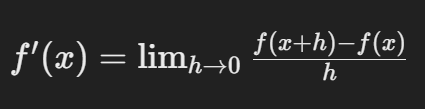
여기서 h는 0에 가까운 아주 작은 변화량이다.
이분은 기하학적으로 함수의 그래프에서 접선의 기울기로 이해할 수 있다.
어떤 함수 y = f(x)의 그래프에서 임의의 점 (x, f(x)) 에서의 접선의 기울기는 f'(x) 이다.
이 기울기는 함수의 변화율을 시각적으로 나타내며, 접선의 기울기가 크면 함수의 변화가 급격하고, 기울기가 작으면
변화가 완만함을 의미한다.
(2) 적분
적분은 미분의 반대 또는 역이다.
적분은 '인테그랄'이라는 기호를 사용한다.

적분이란 어떤 변수의 변화량을 무한히 작은 단위로 나눈 것들을 전부 합산하는 과정이다.
이를 기하학적으로 해석할 시 어떤 함수의 값을 일정 구간에 걸쳐 누적한 면적을 구하는 것으로 생각할 수 있다.
예를 들어, 균등한 두께로 잘린 식빵 덩어리가 있다고 하면
식빵 전체 부피를 구한하고 치면, 각각 빵 조각들의 부피를 하나하나 구한 다음
전부 더해버리면 그게 식빵 전체의 총 부피가 된다.
적분에는 크게 정적분과 부정적분을 구하는 것으로 나뉘는데,
정적분은 특정 구간에서의 함수의 총합을 계산하는 것
부정적분은 함수의 원시함수를 구하는 것이다.
컴퓨터 시뮬레이팅에서는 수학적인 개념의 극한을 사용하지 않고, 대신 매우 작은 이산값들을 사용한다.
이렇게 되면 적분기호를 합산기호 (시그마) 로 바꿔도 문제가 없다.
[7] 질량, 질량중심, 관성모멘트
질량, 질량중심, 관성모멘트. 이들을 통칭하여 질량특성이라고 한다.
물체의 질량특성은 역학 학문에서 매우 중요한 개념이다.
물체의 선운동 (움체의 움직임), 물체의 각운동 (회전 축을 중심으로하는 물체의 회전 운동) 그리고 주어진 힘에 대한 물체 반응 모두 질량특성에 대한 함수이기 때문이다.
따라서 물체의 움직임을 정확히 시뮬레이션하려면 질량특성과 그 계산법에 대해 잘 숙지하고 있어야한다.
먼저, 각각에 대한 기본적인 개념부터 알고 가도록 한다.
(1) 질량

질량은 물리학에서 물질이 가지고 있는 고유한 양을 일컫는 말로
SI 단위에서 '킬로그램'을 사용한다.
역학의 관점에서 질량의 의미를 확장해보자.
뉴턴 제2운동법칙에 따르면 F = ma 이므로, F가 동일할 때 무거운 물체는 가벼운 물체보다 느리게 가속된다.
즉, 질량은 물체가 외부 힘에 대해 얼마나 저항하는지를 나타내는 척도이기도 하다.
질량이 가벼운 물체는 외력에 쉽게 영향을 받기 때문에 운동 상태가 쉽게 바뀔 수 있고,
질량이 무거운 물체는 큰 힘이 아니라면 쉽게 운동 상태가 바뀌진 않을 것이다.
물리학을 잘모르는 관점에서는 '질량'과 '무게'를 헷갈리곤 하는데,
질량은 물체가 가지는 고유한 양이기에 장소에 상관없이 질량은 불변하고 보존된다.
무게는 지구상에서는 질량과 중력가속도 (일반적으로 지오이드 기준 9.806 m/s² 의 값을 사용하지만, 장소에 따라 달라질 수 있다.) 를 곱한 값을 사용한다.
무게의 단위는 N (뉴턴)을 사용하거나 kgf(킬로그램중, 킬로그램힘)을 사용한다.
질량이 60kg 인 사람이 지구에 있을 경우 60kgf 의 무게를 가진다고 하자.
중력가속도가 지구의 1/6인 달로 갔을 경우는 10kgf를 가지게 된다.
하지만 여전히 달에서도 이 사람의 질량은 60kg 이다.
(2) 질량중심
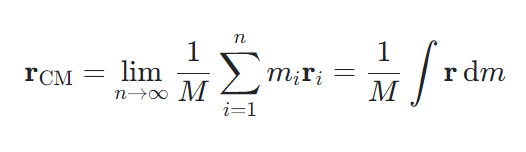
질량 중심은 물체 전체의 질량의 중심점으로, 전체 질량이 질량 중심에 있는 것처럼 외부 계와 작용한다.
물리학에서는 질량 중심이라는 특정한 한 점에 물체나 물체로 이루어진 시스템의 모든 질량이 집중되어 있다고 가정하며, 외부에서 작용하는 모든 힘이 그 점에 작용하는 것처럼 생각한다.
중력이 균일한 경우 무게 중심과 같으므로, 혼용되어 쓰이기도 한다.
역학에서는 질량 중심에 힘을 가해도 회전이 일어나지 않는다는 특징이 있다.
하나 짚고 넘어가야할 용어는 질점 혹은 점질량 (Point Mass) 이다.
어떤 물체를 이루고 있는 미세한 입자중 하나로, 질량은 가지지만 크기(부피)는 가지지 않는 가상의 점이다.
Point Mass 혹은 입자, 파티클이라고 표현하기도 한다.
나중에 한 번 더 다룰 것이긴 하지만
질량 중심 벡터는 각 점질량의 (질량x위치벡터) 에 대한 시그마 값을 전체 질량으로 나누어서 구할 수 있다.
이 공식에서 알 수 있듯 질량이 클 수록 해당 질점으로 질량 중심이 치우치게 된다.
(3) 관성모멘트
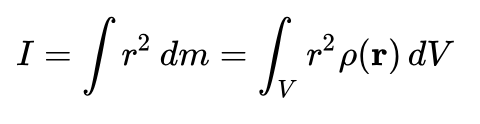
관성모멘트는 물체가 회전 운동을 하는 상태를 계속 유지하려는 성질을 의미하기에, 회전 관성이라고도 부른다.
아마도 모멘트라는 단어가 굉장히 많이 등장할 텐데, 이 용어 먼저 짚고 넘어가자
모멘트는 힘과 그 힘이 작용하는 점에서 기준점까지의 거리의 곱으로 정의된다.
이는 보통 어떤 기준에 대한 "거리 x 물리량" 을 의미한다. '모멘트'라는 것은 그 자체로 특별한 의미를 가지진 않고 주로 '어떤 물리량'이 기준점에서 떨어진 거리에 따라 어떻게 작용하는지를 나타낸다고 볼 수 있다.
가장 기본적은 형태의 모멘트는 다음과 같이 표현된다.

Un 은 '어떤 모멘트'
r는 어떤 기준점에서 물리량이 작용하는 지점까지의 거리
Q는 어떤 물리량을 의미한다.
대표적인 모멘트로는 '힘의 모멘트 (토크 = r x F)', '질량 중심', 관성모멘트, 1차 모멘트, 2차 모멘트 등이 존재한다.
(참고: 힘의 모멘트, 토크, 돌림힘, 회전력은 모두 같은것을 의미한다.)
다시 돌아와서, 관성모멘트는 물체가 자신의 회전 운동을 유지하려는 정도를 나타내는 물리량으로 직선 운동에서 질량에 대응되는 양이다. 통상적으로 기호는 I 를 사용한다.
앞서 질량은 물체가 힘에 저항하는 정도로 해석할 수도 있다고 하였다. 여기서 이 저항 개념을 회전계에서도 적용할 수 있다. 그런데 이 저항의 개념을 회전계에서 그대로 적용하기에는 무리가 있다.
두 개의 질량이 같지만 반지를이 다른 원판 A와 B가 있다고하자. A가 B보다 반지름이 더 크고, 둘 모두 질량 분포가 고르다면, 원반 A를 돌리는 것이 원판 B를 돌리는 것보다 더 어려울 것이다.
즉, 단순 질량만으로는 회전계에서의 관성을 표현하지 못한다는 것.
그래서 회전게에서 힘에 저항하는 요소는 단순히 질량뿐만 아니라 회전하는 위치, 나아가서는 질량중심과 회전축간의 거리도 포함해야 한다는 것이다.
관성 모멘트가 중요한 이유는 회전 운동에서의 질량에 완전히 대응되기 때문이다.
선운동 방정식 F= ma를 예로 들면,
회전계에서의 힘과 각가속도 간의 관계는 τ = Iα 이다.
τ는 토크, I는 관성 모멘트, α는 각 가속도이다.
일반적인 선운동량의 표현식에서 질량이 해주는 일을 관성 모멘트로 대체하면 일관적이고 직관적인 서술이 가능하다.
[8] 질량 특성 계산
(1) 질량 계산
먼저 질량을 계산하는 과정은 다음과 같다.
수많은 입자로 구성되어 있는 물체가 있다고 생각해보자.
이 물체의 총 질량은 그 물체를 구성하는 각 입자의 질량을 모두 합한 것 과 같다.

어떤 물체의 질량은 위 공식으로 구할 수 있다.
(중고교과정에서 배웠던 밀도의 공식인, '밀도 = 질량/부피' 을 상기하면 도움이 된다.)
따라서 밀도가 균일하게 분포되어 있는 물체의 총 질량은 (물체의 밀도) x (물체의 총부피)와 같다.
이것을 수식으로 써보면 질량에 대한 식을 얻어 낼 수 있다.
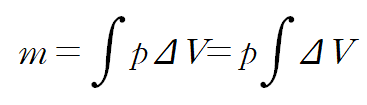
사실 물체의 질량을 구하기 위해 부피를 적분해야 할 일은 거의 없다.
복잡한 물체의 경우 다양한 밀도로 구성되어 있기에 적분이 까다로울 수 밖에 없다.
따라서 비행기, 자동차 등의 부피를 구할 때는 부품 단위로 분해해서 질량을 따로따로 계산한 뒤, 그 부분질량을 모두 다 더하는 방법이 훨씬 낫다.
(2) 무게중심 좌표 계산
이제 무게중심을 계산해보자.
무계중심을 계산하려면 우선 물체를 유한 개의 작은 부분으로 나눈다.
앞서 말했듯 이것을 점질량(point mass)라고 부를 것이다.
어떤 물체의 무게중심 좌표를 계산하기 위해서는 먼저 해당 물체의 1차 모멘트 값을 구해야 한다.
1차 모멘트는 물체의 한 점을 기준으로 질량이나 면적이 그 점에 대해 어떻게 분포되어 있는지 나타내는 값이다.
우리가 사용할 것은 질량 1차 모멘트이다.
어떤 물체의 질량 1차 모멘트 벡터를 구하는 방법은
물체를 이루는 질점에 대하여 각 좌표축과 원점 사이의 위치벡터를 구한 뒤 질량을 스칼라 곱셈하고 이 결괏값을 모두 더하면 된다.
질점 i의 질량을 mi와 위치벡터를 ri = (xi, yi, zi) 라고 할 때, 어떤 물체의 질량 1차 모멘트 벡터 G은 다음과 같이 정의된다.
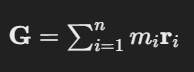
이제 물체의 1차 모멘트를 총 질량으로 나누면 물체의 질량중심까지의 좌표를 구할 수 있다.
이 계산은 각 좌표축마다 한 번 씩 해야한다.
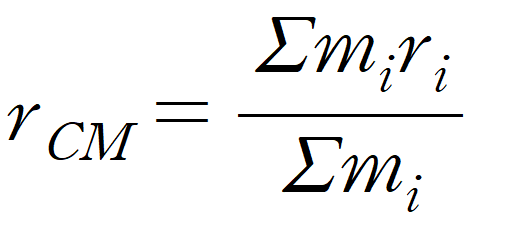
최종적인 물체의 질량중심의 좌표를 구하는 공식이라고 할 수 있겠다.
물론 이론적으로는 시그마를 사용하지 않고 적분기호를 사용한다.
그러나 시뮬레이션에서는 유한 개의 질량을 더할 것이기에 시그마를 사용해도 전혀 상관이 없다.
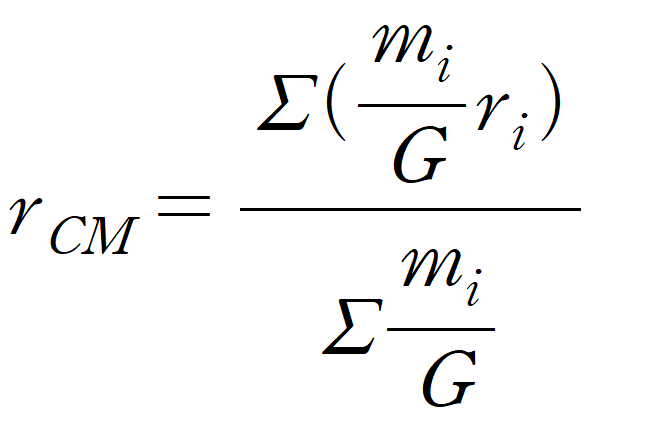
여기서 한가지 재밌는 사실은 물체의 질량을 물체의 무게로 치환해도 전혀 상관이 없다는 것이다.
어차피 중력가속도는 상수로 취급하는 경우가 많기에 이것을 약분하면 남는 것은 질량이기 때문이다.
아래는 점질량으로 전체 무게중심 좌표를 구하는 공식이다.
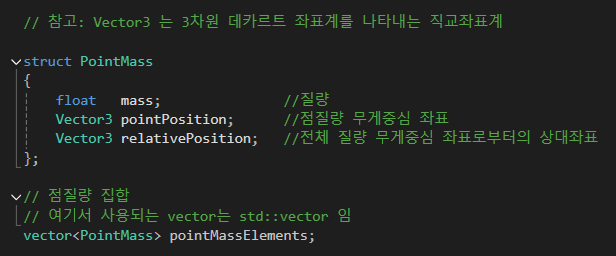
점질량을 구조체로 정의하여 점질량 배열을 만든다.
점질량 구조체에는 각 점질량의 좌표와 질량을 담고 있다.
또한 현재 점질량에서 물체의 최종 무게중심까지의 거리를 저장하기 위한 변수도 하나 존재한다.
다른 말로 하면 무게중심으로부터 점질량의 상대 좌표라고 설명할 수 있다.
(물론 이 값을 구하여면 최종 무게중심을 계산해야 하기에 나중에나 얻을 수 있는 값이다.)
먼저 점질량 구조체 먼저 살펴보자.
다음은 총 질량과 최종 무게중심을 구하는 코드이다.
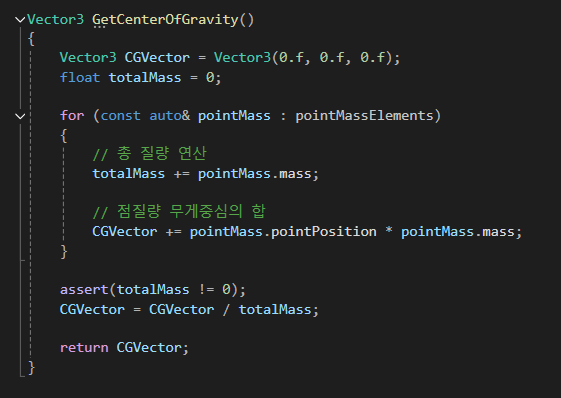
여기서 앞서 구조체에서 설정한 상대좌표를 까지 구해보면 코드는 다음과 같다.

[관련 코드]
#include "pch.h"
// 참고: Vector3 는 3차원 데카르트 좌표계를 나타내는 직교좌표계
struct PointMass
{
float mass; //질량
Vector3 pointPosition; //점질량 무게중심 좌표
Vector3 relativePosition; //전체 질량 무게중심 좌표로부터의 상대좌표
};
// 점질량 집합
// 여기서 사용되는 vector는 std::vector 임
vector<PointMass> pointMassElements;
Vector3 GetCenterOfGravity()
{
Vector3 CGVector = Vector3(0.f, 0.f, 0.f);
float totalMass = 0;
for (const auto& pointMass : pointMassElements)
{
// 총 질량 연산
totalMass += pointMass.mass;
// 점질량 무게중심의 합
CGVector += pointMass.pointPosition * pointMass.mass;
}
assert(totalMass != 0);
CGVector = CGVector / totalMass;
for (auto& pointMass : pointMassElements)
{
// 상대좌표 계산
pointMass.relativePosition = pointMass.pointPosition - CGVector;
}
return CGVector;
}
int main() {
pointMassElements.push_back({ 2.0f, Vector3(1.0f, 2.0f, 3.0f) });
pointMassElements.push_back({ 3.0f, Vector3(4.0f, 5.0f, 6.0f) });
pointMassElements.push_back({ 5.0f, Vector3(7.0f, 8.0f, 9.0f) });
Vector3 centerOfGravity = GetCenterOfGravity();
std::cout << "Center of Gravity: (" << centerOfGravity._x << ", " << centerOfGravity._y << ", " << centerOfGravity._z << ")\n";
for (const auto& pointMass : pointMassElements) {
std::cout << "Relative Position: (" << pointMass.relativePosition._x << ", " << pointMass.relativePosition._y << ", " << pointMass.relativePosition._z << ")\n";
}
return 0;
}
(3) 질량관성모멘트 계산
관성모멘트의 값은 물체의 질량 분포가 '축'에 대해 어떻게 분포되어 있는지에 따라 달라진다.
3차원에서 관성 모멘트를 계산하려면 물체를 구성하는 각 질점의 2차모멘트를 구해야 한다.
2차 모멘트는 물체가 특정 축에 대해 얼마나 저항하는지를 나타내는 값이다.
3차원에서의 2차 모멘트는 각 좌표축 (x, y, z)에 대해 개별적으로 계산되며, 이는 물체가 각 축을 중심으로 회전할 때 저항하는 정도를 나타낸다.

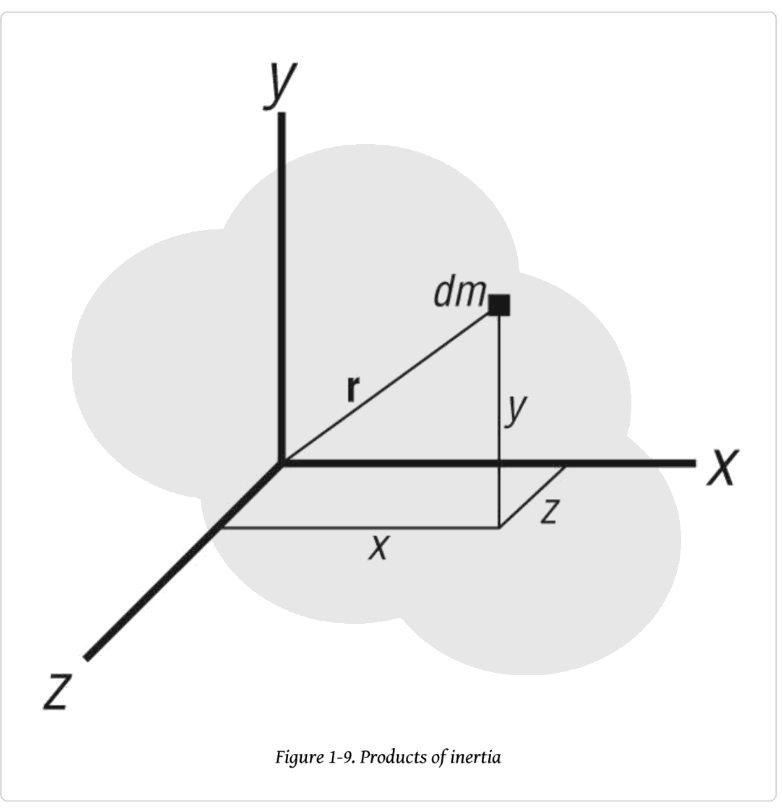
점 질량의 질량을 m, 계산하려는 축에 대해 그 축까지의 수직 거리를 r 이라고 하자.
그렇다면 2차 모멘트는 (질량) X (회전축과의 수직거리)² 으로 구할 수 있다.
여기서 주의할 점은 거리 r은 질량중심을 구할 때 사용하는 거리와 사뭇 다르다는 것이다.
질량중심을 구할 때는 원점으로 부터의 위치 벡터를 사용했지만,
2차 모멘트를 계산할 때는 축에 대한 최단거리를 사용한다.
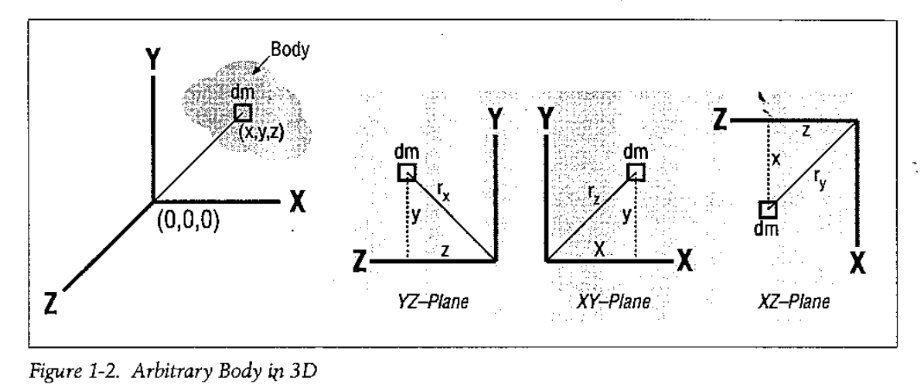
그러므로 어떤 질점의 위치벡터가 (x, y, z)라고 하고 x축을 회전축으로 한 2차 모멘트를 구하고자 한다면
r² = y² + z² 가 된다.
(참고로 2차 모멘트는 스칼라 값이다.)
특정 축에 대한 관성모멘트는 해당 물체의 특정 축에대한 2차 모멘트의 적분으로 구할 수 있다.
간단하게 식으로 표현하면 다음과 같다.
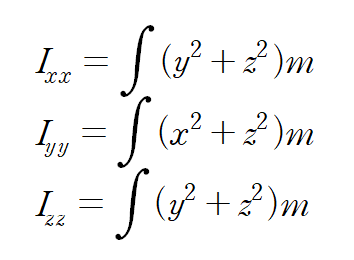
위 식은 위에서부터 차례대로
x축을 회전축으로 하는 관성모멘트, y축을 회전축으로 하는 관성모멘트, z축을 회전축으로 하는 관성모멘트이다.
이제 다른 상황을 상상해보자.
위 관성모멘트는 어떤 물체가 있고 그 물체의 질량중심을 관통하는 축 (이런 축을 중립축이라 한다.)
하지만 많은 실제 응용에서는 물체가 질량 중심이 아닌 '특정한 축'을 기준으로 회전한다.
예를 들어, 문은 경첩을 기준으로 회전하지 문 자체의 질량 중심으로 회전하지 않는다.
그렇다면 중립축과 평행하지만 약간 거리가 떨어져 있는 다른 축을 기준으로 관성 모멘트를 구하고 싶다면 어떻게 해야할까? 이럴 때는 평행축 정리를 이용할 수 있다.
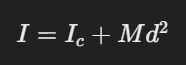
I는 새로운 관성 모멘트
Ic는 질량 중심을 지나는 축에 대한 관성 모멘트
M은 물체의 전체 질량
d는 질량 중심 축과 새로운 축 사이의 거리
를 뜻한다.
평행축의 정리를 유도하는 과정은 다음과 같다.

한 가지 주목할 점이 있는데, 이 새로운 관성모멘트는 두 축 간의 거리의 제곱에 대한 함수이다.
즉, Io의 값이 d에 비해 작다면 무시해도 큰 문제가 없다는 의미이다.
이런 경우 md² 가 위 공식의 결과에 결정적인 영향을 미치게 된다.
(물론 약간의 오차는 생기기 마련이다.)
위 평행축 정리 공식에서 알 수 있는 또 다른 사실 하나는 최소 관성모멘트를 구하려면 물체의 무게중심을 통과하는 축 주위의 관성모멘트를 취하면 된다는 것이다.
그렇다면 중립축과 다른 축이 같은 것이라 d가 0이 되기 때문이다.
그 외의 축에서 관성모멘트를 계산하면 그 결괏값이 md²에 비례해서 증가하게 된다.
이렇듯 단일밀도를 가지고 모양이 매우 단순한 물체의 질량관성모멘트를 구하는 것은 쉬운 편이다.
하지만 그렇지 않은 물체의 질량관성모멘트를 구하는 건 다른 이야기다.
이런 경우에는 흔히 그 물체와 유사하게 생긴 다른 단순한 기초도형들을 이용해 근사치를 구한다.
아니면 물체들을 여러 부분으로 나누어서 각 부분들의 관성모멘트를 구하기도 하는데, 이때 중립축에서 멀리 떨어진 부분들에 대해서는 Io를 생략하는 방법으로 공식을 단순화할 수 있다.
앞서 말했듯 평행축 정리는 md²의 영향력이 매우 크기 때문이다.
물론 생략하여 생기는 오차를 어떻게 할 것인지는 스스로 판단해야 한다.
다음은 흔히 쓰이는 기초도형들의 예이다.
이 물체들은 전부 단일밀도이므로 쉽게 질량관성모멘트를 계산할 수 있다.
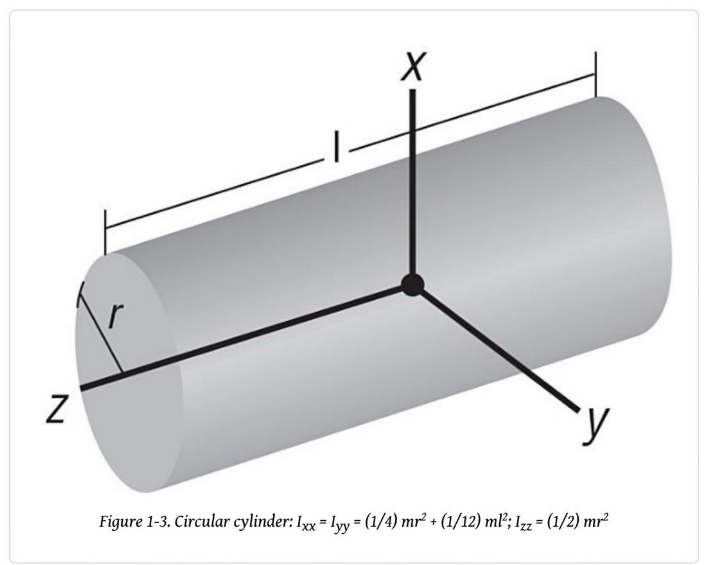
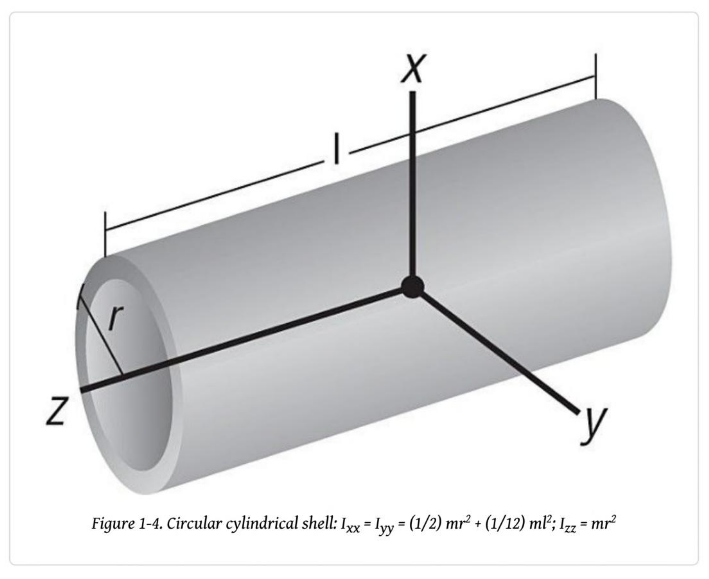
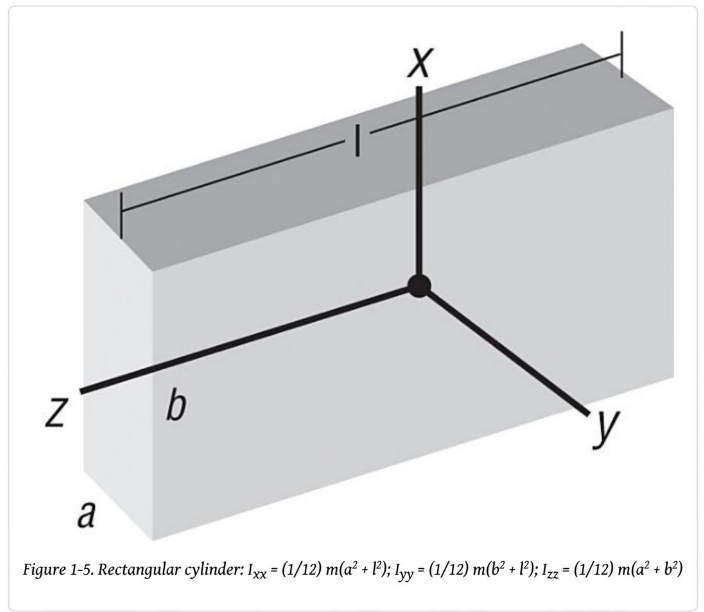

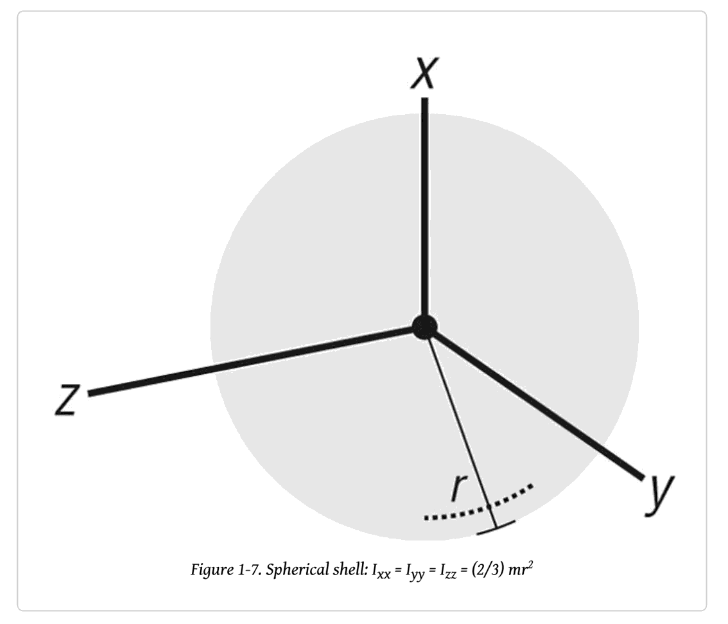
당연하게도 회전축을 어떻게 잡냐에 따라 관성 모멘트는 달라질 수 있다.
위 도형들의 공식은 비교적 쉽게 구현할 수 있으므로 복잡한 물체의 관성을 구할 때는 이것들을 조합하여, 각각의 관성 값을 구해 합산하면 된다.
물론 이것은 근삿값일 뿐 오차허용 범위에 따라 이 방법의 사용 여부를 결정해야 한다.
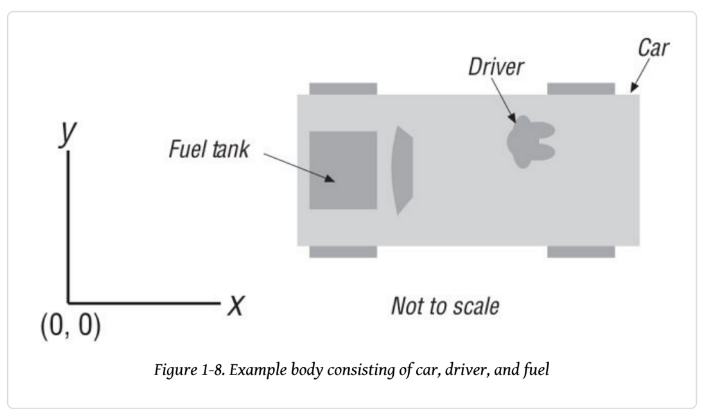
그럼 간단한 2D 예를 들어 이 절에서 살펴본 공식을 사용해보자.
탑다운 뷰 시점의 자동차 경주 게임을 만들다고 가정하자.
그러면 2D 리지드바디 동역학을 이용해 자동차의 움직임을 시뮬레이션 할 수 있을 것이다.
자동차에는 자동차, 운전자, 연료가 존재하고 각각의 질량을 계산해야 한다.
연료가 소모되거나 운전자가 없어지면 그만큼 전체 질량이 들어들 것이다.
지금은 일단 초기 상태만 신경쓰도록 하자.
위 그림에 있는 각 구분의 물리적 특성들은 다음과 같다.
여기서 길이는 x축, 너비는 y축이다. 그리고 탑다운 뷰이므로 높이는 화면 바깥쪽(-z축)을 가리킨다.
또한 각 구성부분의 중점을 나타내는 좌표 (x, y)가 존재한다.
| 자동차 | 운전자 (앉아있음) | 연료 |
| 길이 = 4.7m | 길이 = 0.90 m | 길이 = 0.50 m |
| 너비 = 1.80m | 너비 = 0.50 m | 너비 = 0.90 m |
| 높이 = 1.25m | 높이 = 1.10 m | 높이 = 0.30 m |
| 무게 = 17,500 N | 무게 = 850 N | 연료의 밀도 = 750 kg/m² |
| 중심 = (30.5, 30.5) m | 중심 = (31.50, 31.00) m | 중심 = (28.00, 30.50) m |
첫 번째로 구할 것은 물체의 질량이다.
이미 차와 운전자의 무게를 알고 있으니 별로 어렵지 않다.
유일하게 무게를 계산해야 하는 것은 연료인데,
연료의 밀도와 부피를 알고 있으니 쉽게 구할 수 있다.
연료의 모양은 육면체꼴이고
그 부피는 0.50 * 0.90 * 0.30 = 0.135 m³ 이다.
무게 = 부피 * 밀도 * 중력가속도 이므로
0.135 * 750 * 9.81 = 약 993 N 이다.
이제 물체의 총 무게를 구할 수 있으며 그것은 다음과 같다.
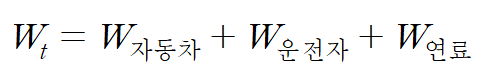
Wt = 17500 + 850 + 993 = 19343 N
물체의 질량을 구하려면 물체의 총 무게를 중력가속도로 나누면 된다.
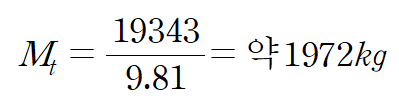
이제 물체의 무게중심 좌표를 구해보도록 하자.
무게중심 좌표를 구하는 방법은 위에서 다뤘기에 간단하게 과정만 풀이한다.

이 식에서 질량 대신 무게를 사용했는데 괜찮을까?
이것이 가능한 이유는 무게 = 질량x중력가속도 이기 때문이다.
이것은 약분할 수 있기에, 무게를 사용해서 계산하더라도 무리는 없다.
이제, 물체의 질량관성모멘트를 구해보자.
해당 예제는 회전축이 물체의 높이방향 하나밖에 없기 때문에 계산이 매우 간단하다.
우선 각 요소들 간의 로컬 관성모멘트를 계산할 것이다.
관성모멘트의 회전축은 각 구성부분의 중립축이다.
각 구성부분의 형태에 대한 질량 분포 및 형태 등을 정의되어 있지 않은데,
질량관성모멘트는 물체의 형태와 질량 분포, 밀도 등.. 에 영향을 받으므로 이에 대한 정의는 필수적이다.
일단 이 예제에서는 계산을 쉽게하기 위해서 각 구성을 직육면체라고 가정하겠다.
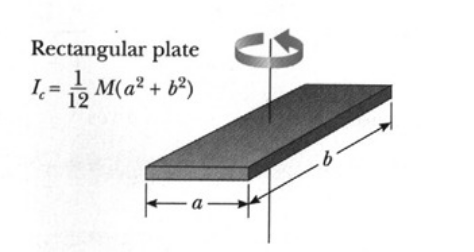
그렇다면 위 공식을 통해서 관성모멘트를 구할 수 있게 된다.

이들은 각 구성부분의 중립축 주위의 관성모멘트이므로 이제 평행축 정리를 이용해 물체의 중립축(무게중심좌표)으로 전송해야 한다.
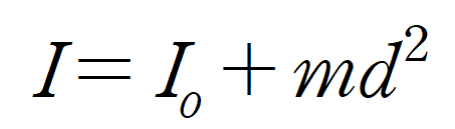
그러면 물체의 무게중심으로부터 각 구성부분의 무게중심까지의 거리를 구해야 한다.
이는 단순한 점과 점 사이의 거리 공식으로 구할 수 있을 것이다.
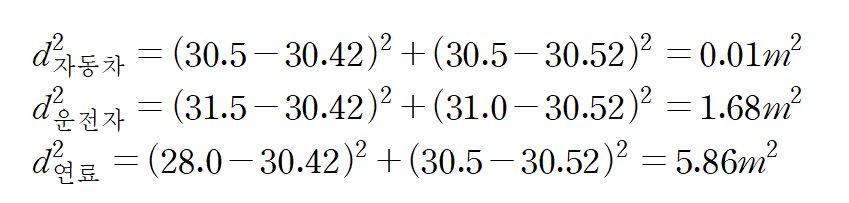
이제 평행축 정리를 이용해보자

(운전자와 연료의 평행축 정리 결과 md² 의 영향력이 매우 큰 것을 알 수 있다.)
마침내 전체 질량관성모멘트를 구할 수 있게 되었다!
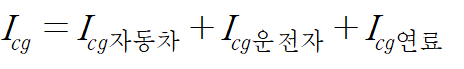
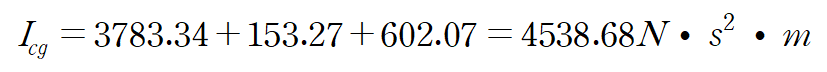
물체의 질량특성 (자동차, 운전자, 연료를 고려한) 은 다음과 같습니다.
| 특성 | 계산 결과 |
| 총 질량 | 1972 kg (19343 N) |
| 질량의 무게중심 좌표 | (x, y) = (30.42m, 30.53m) |
| 질량관성모멘트 | 4538.68 Ns²m |
해당 예제는 2차원 공간이었지만 3차원 공간에서 일반적인 운동을 다룰 때는 식이 훨씬 더 복잡해질 것이다.
물체의 운동은 이 질량특성들의 함수이다. 질량은 물체가 힘에 어떻게 반응하는지를 결정하고, 질량중심은 물체의 위치를 구할 때 사용하며, 질량관성모멘트는 질량중심이 아닌곳에 힘이 가해질 때 물체의 회전을 계산한다.
3D 리지드바디 동역학을 다루면 관성모멘트의 공식은 더욱 복잡해지지만 일단 이에 대해서는 후에 살펴보도록 한다.
2. 뉴턴의 제2운동법칙
뉴턴의 제2운동법칙은 역학 분야에서 특별한 의미를 가진다.
뉴턴의 제2운동법칙 방정식은 다음과 같다.

여기서 F는 물체에 작용하는 힘의 합이고, m은 물체의 질량, a는 질량중심에서의 선가속도이다.
이제 양변을 m으로 나눠보자.

이 식을 보면 질량이 물체의 운동을 방해하는 요인이 된다는 사실을 알 수 있다.
물체가 받는 힘이 일정하다면, 분모에 있는 질량이 늘어남에 따라 물체의 가속도가 줄어들 것이다.
이는 질량이 큰 물체일수록 움직이기 어렵다는 이야기이기도 하다.
마찬가지로 힘이 일정할 때 질량이 감소한다면 물체의 가속도가 늘어난다.
질량이 작은 물체는 움직이기가 쉽다.
뉴턴의 제 2운동법칙에 따르면 물체가 받는 힘의 방향과 가속의 방향은 같다고 한다.
여기서 '방향'이라는 개념이 나왔기에 힘과 가속은 모두 벡터여야 한다.
보통 물체가 받는 힘은 여러 가지이다.
중력, 마찰력, 탄성력, 장력, 외력 등..
이 때 모든 힘의 벡터합을 구하면 최종 합력을 의미한다.
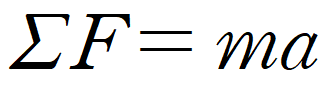
3D에서 힘과 가속도 벡터는 직교좌표계 내에서 x, y, z 값을 가진다.
이때 각 성분의 운동방정식은 다음과 같다.
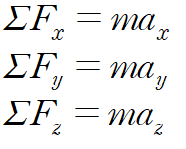
뉴턴의 제 2운동법칙은 '물체가 받는 모든 힘의 합은 선운동량 변화량과 같다.' 라고 해석할 수도 있다.
즉, 물체에 작용한 힘은 운동량을 시간으로 미분한 결과이다.

운동량은 질량 x 속도이고, 속도와 운동량은 모두 벡터이므로 다음과 같은 식을 만들 수 있다.
자 그럼 이를 시간에 대해서 미분해보자.
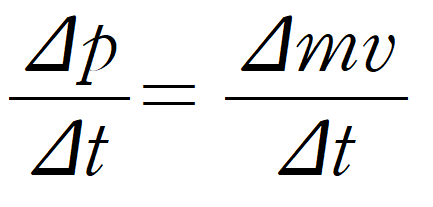
여기서 질량은 일정하다고 가정하면 다음과 같이 식을 변형할 수 있다.
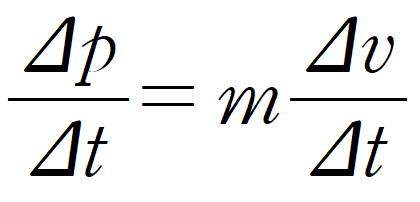
여기서 속도의 변화량은 곧 가속도를 말하니 최종적으로 식이 다음과 같아진다.

여태까지 우리가 다룬 물체의 운동은 평행이동뿐이었다.
그러나 3D 운동에는 회전운동도 포함된다.
그럼 물체의 움직임을 제대로 표현하기 위해 방정식을 몇 개 추가해보겠다.
구체적으로 말하면, 모든 모멘트의 합과 회전운동량의 변화율 사이의 관계를 구하는 공식이 필요하다.

간단히 말하면 토크를 구하고자 하는 것이다.
여기서 τ는 물체의 무게중심 주위를 회전하는 모든 모멘트의 합이고,
L는 각운동량이다.
각운동량 L는 다음과 같이 쓸 수 있다.
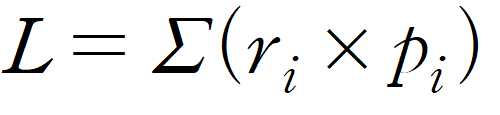
어떤 물체의 각운동량은 질점의 무게중심벡터로 부터의 상대좌표와 선운동량의 외적의 합이다.
p = mv로 풀어서 사용할 수 있고
선속도v는 각속도w와 v = rㆍw 의 관계를 가진다.
이에 맞게 식을 고치면 아래와 같다.
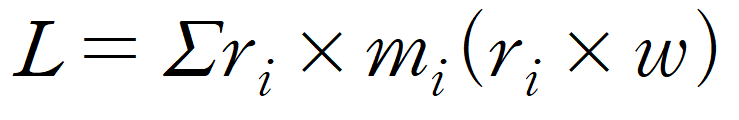
식이 조금 복잡해졌지만 다시 상기하자면
시그마 내부는 질점 i의 각운동량을 의미한다.
이 식을 고쳐서쓰면 아래와 같다.

각속도 w는 각 질점마다 동일하므로 상수로 취급될 수 있다.
앞서 r²m의 적분이 관성모멘트를 의미한다는 것을 기억하는가?
그렇다면 각운동량은 최종적으로 아래와 같이 나타낼 수 있다.
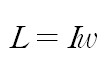
이 공식 언뜻보기에 선운동량 공식과 비슷해보이지 않는가?
그렇다 선운동량 공식에서 질량 -> 관성모멘트, 선속도 -> 각속도로 바꾼 것과 동일하다.
이제 이 수식을 미분해보자.
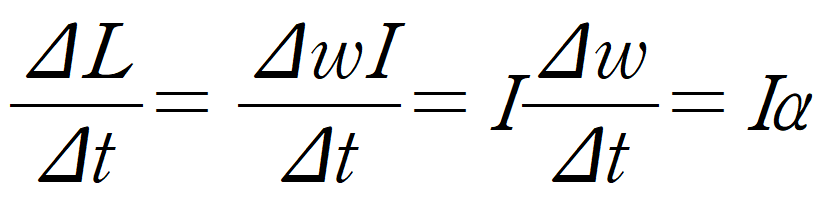
결국 간략화시킬 수 있게 되었다.
최종적으로 토크와 각운동량 변화량의 관계식은 아래와 같다.
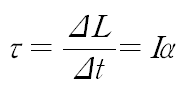
이 공식도 가속도 공식이랑 매우 유사하다.
관성모멘트는 어떤 물체축 주위의 회전이라도 처리할 수 있어야 한다.
그러므로 관성모멘트와 각모멘트 공식들을 좀 더 일반화 해야한다.
보통 토크와 각가속도는 벡터 값이다.
한편, 물체의 관성모멘트의 크기는 회전축에 따라 달라질 수 있으므로 관성모멘트 I는 '텐서' 여야만 한다.
[참고 '텐서']
텐서는 크기와 방향을 가지는 수학표기법이다.
그런데 텐서의 크기는 방향에 따라 값이 달라질 수도 있어서 이런 물질의 특성을 나타내기 위해 흔히 사용된다.
이렇게 방향에 따라 다른 특성을 갖는 물질을 이방성 이라 한다.
이와 반대로 등방성은 모든 방향에서 같은 크기를 가진다.
정사각형 색종이를 생각해보자.
어떤 방향으로 잡아당기든 종이의 탄성이 변하지 않는다.
이런 것이 등방성이고, 단 하나의 스칼라 값으로 모든 방향에 대한 강도를 나타낼 수 있다.
넥타이와 같은 격자무늬로 짜여진 느슨한 천 조각을 생각해보자.
아무래도 격자방향이 아니라 대각선으로 잡아당기면 더 많이 늘어날 것이다.
이 천은 잡아당기는 방향에 따라 탄성이 달라지니 이방성이다.
이 경우 몯느 방향으로의 힘을 표현하려면 여럿 벡터(텐서라고 부를 수 있다.) 가 필요하다.
앞서 말했던 관성모멘트는 텐서이다.
임의의 회전에서 3D 관성모멘트를 나타내려면 총 9개의 성분이 필요하다.
그렇기 때문에 관성모멘트는 3x3 행렬로 일반화 시킬 수 있고 이를 2차 텐서라고 부른다.
참고로 벡터는 1차 텐서, 스칼라는 0차 텐서이다.
지금까지 다루었던 두 가지 운동방정식은 로컬공간 좌표가 아니라 월드공간 좌표를 이용했다.
선운동방정식에선 이래도 상관 없다.
어차피 월드공간 안에서 물체의 위치와 속도를 구하기 때문이다.
그러나 각운동방정식에서 이러면 계산량이 너무 많아진다.
2차원에서는 관성모멘트가 스칼라 상수이기 때문에 큰 문제가 되지 않으나,
3차원공간 좌표를 사용해서 관성모멘트를 계산하면 물체의 위치와 방향에 따라 이 값이 바뀌기 때문이다.
즉슨, 관성행렬은 3x3 행렬인데 매 틱 이러한 행렬을 계산해야 한다는 것이다.
이것은 꽤 비효율적이다.
차리라 운동방정식을 수정해서 각운동방정식은 로컬 공간 좌표를 사용하는 편이 낫다.
그러면 시뮬레이션을 시작할 때 딱 한 번만 관성행렬을 계산하면 되기 때문이다.
일반적으로 고정좌표계에서의 벡터 V에 대해서
고정좌표계의 V 시간미분은 회전좌표계의 V 시간미분과 다음의 관계를 가진다.
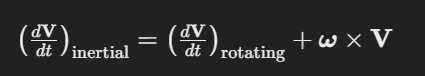
이 관계를 이용하여 각운동방정식을 로컬좌표계로 변환할 수 있다.
여기서 각 운동량벡터 L = Iw 를 대입해 보겠다.
각 운동량벡터를 미분하면
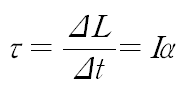
이러한 식을 갖게 된다는 것을 위에서 알아봤다.
이를 대입하면 다음과 같다.
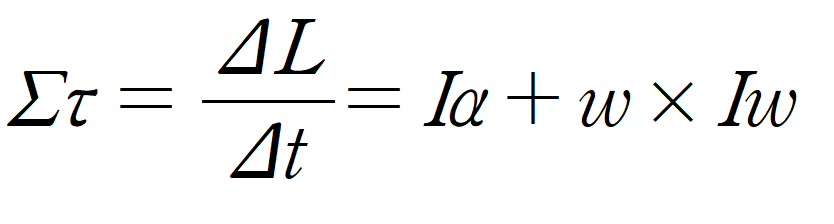
여기서 조금 더 수정하여 실전에서는 아래와 같은 식을 사용할 것이다.
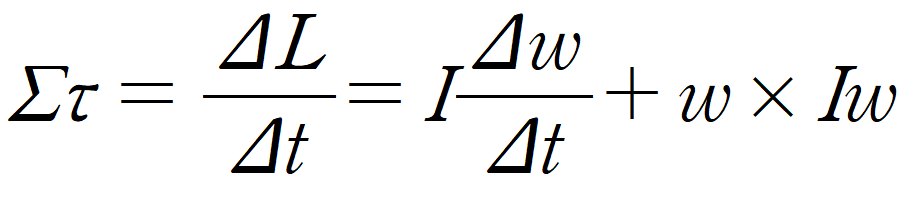
이 식에서 모멘트, 관성텐서(관성모멘트), 각운동량은 모두 로컬공간에 있다.
식이 조금 더 복잡해지긴 했지만 시뮬레이션 중에 I가 전형 변하지 않으므로 훨씬 사용하기 편한 공식이다.
더하여 로컬좌표계에서 모멘트를 계산하는 것이 더 쉽다.
3. 관성텐서
관성 텐서는 기존 관성 모멘트가 회전축에 따라 달라지는 것을 보완하고, 평면상의 강체 회전뿐만 아니라 3차원상의 회전을 기술하기 위한 관성 모멘트에 대응하는 물리량이다.
2차원 문제에서 관성은 결국 단일 축 주위의 관성모멘트를 타나내기에 스칼라 값이 된다.
그러나 3차원의 경우에는 물체가 회전할 수 있는 좌표축이 셋으로 늘어난다.
게다가 일반적인 3차원 공간에서는 물체는 아무 축 주위나 회전할 수 있다.
따라서 3차원 문제에서 관성 모멘트 I는 3x3 행렬 (즉, 2차텐서) 이다.
그럼 관성행렬을 만들어보도록 하자.
각 운동량 방정식을 다시 보도록 하자

괄호안에 있는 것은 삼중 벡터곱으로서 외적 연산을 통해 전개할 수 있다.
참고로 삼중 벡터곱이란
A X ( B X C ) = B(AㆍC) - C(A ㆍ B) 가 성립함을 말한다.
r과 w는 다음과 같은 벡터이다.
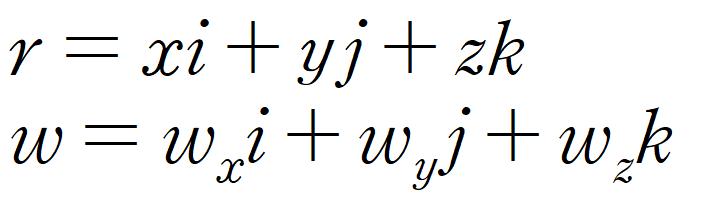
위 식의 세 벡터곱을 확장하면 식이 다음처럼 된다.

(식 도출 과정이 계산이 복잡하여 간단하게 답만 정리하였다.)
각 축을 기준으로 9개의 관성모멘트는 다음과 같이 구할 수 있다.
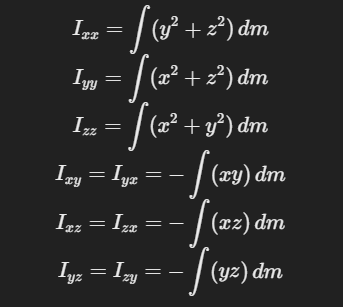
이를 이전 식에 대입해보면 다음과 같다.
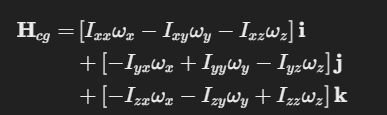
이제 한 단계 더 나아가 I를 다음과 같은 행렬이라고 치자.
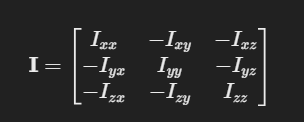
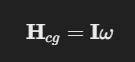
그러면 공식을 매우 간단하게 바꿀 수 있다.
Ixx, Iyy, Izz 는 세 좌표축 주위의 관성모멘트고
나머지 비대각성분 항을 관성곱이라고 한다.
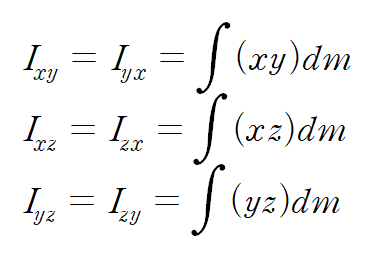
평행축 정리와 마찬가지로 관성곱에 적용할 수 있는 평행축 정리는 다음과 같다.
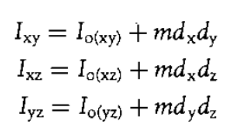
여기서 Io 항은 로컬 관성곱 (물체의 무게중심을 관통하는 축 주위의 관성곱) 이며, m은 물체의 질량
d는 물체의 무게중심을 통과하는 좌표축과 그에 평행한 다른 축 사이의 거리이다.

앞서 설명했던 각 기초도형의 관성모멘트를 구하는 공식이다.
각 기초도형의 관성곱 공식을 소개하지 않은 이유는 관성곱 성분이 0이었기 때문이다.
3차원상에서 강체의 회전 운동 시 각운동량과 각속도는 서로 반드시 평행하진 않는다.
그러나 특정 축에서는 이들이 평행할 수 있다.
평행하다는 의미는 관성곱이 0이라는 의미이다.
그러한 특정 축을 관성 주축이라고 한다.
도형이 주축을 기준으로 회전할 경우 주축 주변의 질량이 균일하게 분포되어 있기에 관성곱 항의 값이 모두 0이 된다.
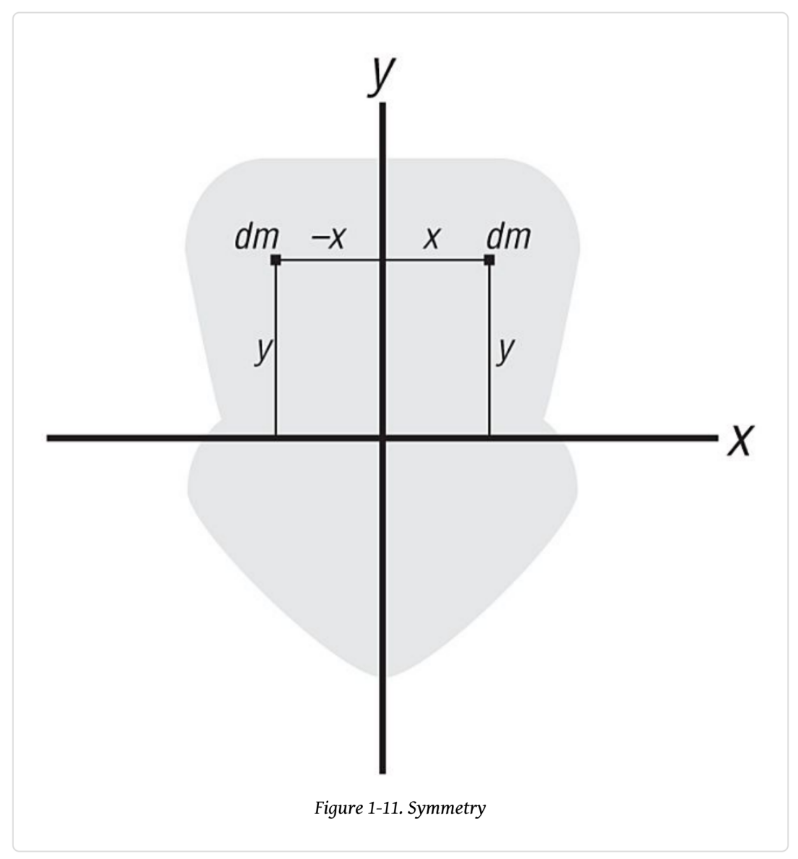
이를 이해하기 위해서 대칭도형을 준비하였다.
대칭 도형의 경우 회전축이 대칭 축을 기준으로 정의되면 관성곱이 0이 되게 된다.
이는 대칭 축을 기준으로 항 싼의 대칭 질량 요소들이 상쇄되기 떄문이다.
예를 들어 모든 xy항은 -xy항에 의해 지워지게 된다.
한편 어느 평면에도 대칭이지 않은 물체도 있다.
물론 이런 평면에도 주축은 존재하지만, 주축을 정확히 찾기는 어렵다.
게다가 주축을 강체(이하 리지드바디)의 로컬좌표축으로 쓰기도 꽤 어려우니 차라리 안 그러는게 나을 것이다.
예를 들어서 어떤 비행기 시뮬레이션을 생각해보자.
비행기 시뮬레이션에서는 편의를 위해 주축과 상관없는 좌표축을 사용한다.
이를테면 파일럿을 기준으로 전후/상하/좌우 방향의 로컬 좌표축을 설계하는 것이다.
이는 직관적으로 이해하기는 쉽지만 실체 비행체의 주축은 아니기 때문에,
이 시스템에서 관성텐서를 구하면 관성곱이 0이 아니고, 이를 따로 처리해줘야한다.
이 때는 관성 모멘트 텐서를 대각화하는 방법을 사용한다.
대각화를 하면 주대각선 외의 모든 원소가 0인 행렬로 만들 수 있는데,
이때 구해지는 고윳값이 관성 모멘트에 해당하게 되고, 또한 고유벡터가 곧 주축에 대응하게 된다.
아래는 관성 모멘트 텐서를 구하는 코드이다.
여러 부분으로 구성된 복합체의 관성모멘트의 합을 계산하는 방법은 이미 앞에서 설명했다.
각각 로컬 관성모멘트를 구한뒤 평행축 정리를 이용한 뒤 결괏값을 모두 더하면 된다.
관성 텐서를 구하는 과정도 역시 동일하다.
평행축 정리의 특성과 유사하게, 관성 텐서 계산에 가장 큰 영향을 미치는 것은 축전송 항이 된다.
아래 점질량 구조체에 로컬 관성모멘트 멤버를 추가해보겠다.

아래는 관성곱들을 계산하는 코드이다.
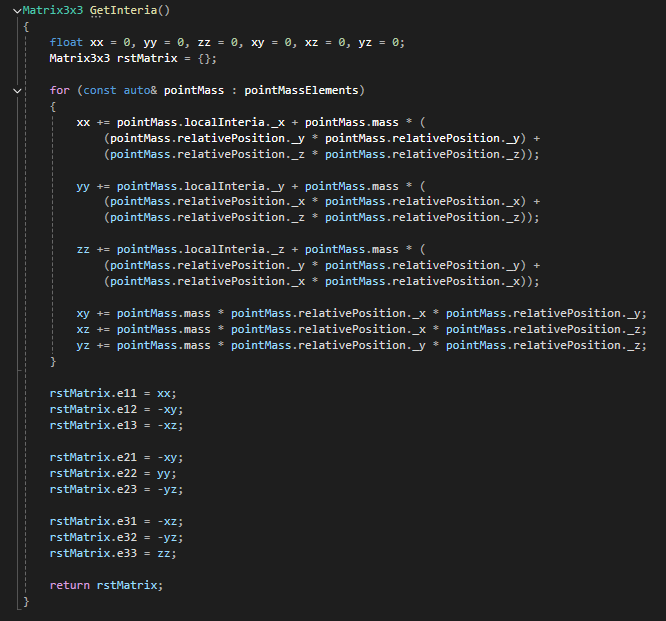
[전체코드]
#include "pch.h"
// 참고: Vector3 는 3차원 데카르트 좌표계를 나타내는 직교좌표계
struct PointMass
{
float mass; //질량
Vector3 pointPosition; //점질량 무게중심 좌표
Vector3 relativePosition; //전체 질량 무게중심 좌표로부터의 상대좌표
Vector3 localInteria; //로컬 관성모멘트
};
// 점질량 집합
// 여기서 사용되는 vector는 std::vector 임
vector<PointMass> pointMassElements;
Vector3 GetCenterOfGravity()
{
Vector3 CGVector = Vector3(0.f, 0.f, 0.f);
float totalMass = 0;
for (const auto& pointMass : pointMassElements)
{
// 총 질량 연산
totalMass += pointMass.mass;
// 점질량 무게중심의 합
CGVector += pointMass.pointPosition * pointMass.mass;
}
assert(totalMass != 0);
CGVector = CGVector / totalMass;
for (auto& pointMass : pointMassElements)
{
// 상대좌표 계산
pointMass.relativePosition = pointMass.pointPosition - CGVector;
}
return CGVector;
}
Matrix3x3 GetInteria()
{
float xx = 0, yy = 0, zz = 0, xy = 0, xz = 0, yz = 0;
Matrix3x3 rstMatrix = {};
for (const auto& pointMass : pointMassElements)
{
xx += pointMass.localInteria._x + pointMass.mass * (
(pointMass.relativePosition._y * pointMass.relativePosition._y) +
(pointMass.relativePosition._z * pointMass.relativePosition._z));
yy += pointMass.localInteria._y + pointMass.mass * (
(pointMass.relativePosition._x * pointMass.relativePosition._x) +
(pointMass.relativePosition._z * pointMass.relativePosition._z));
zz += pointMass.localInteria._z + pointMass.mass * (
(pointMass.relativePosition._y * pointMass.relativePosition._y) +
(pointMass.relativePosition._x * pointMass.relativePosition._x));
xy += pointMass.mass * pointMass.relativePosition._x * pointMass.relativePosition._y;
xz += pointMass.mass * pointMass.relativePosition._x * pointMass.relativePosition._z;
yz += pointMass.mass * pointMass.relativePosition._y * pointMass.relativePosition._z;
}
rstMatrix.e11 = xx;
rstMatrix.e12 = -xy;
rstMatrix.e13 = -xz;
rstMatrix.e21 = -xy;
rstMatrix.e22 = yy;
rstMatrix.e23 = -yz;
rstMatrix.e31 = -xz;
rstMatrix.e32 = -yz;
rstMatrix.e33 = zz;
return rstMatrix;
}
int main() {
pointMassElements.push_back({ 17500.0f, Vector3(30.5f,30.5f,0.f) });
pointMassElements.push_back({ 850.0f, Vector3(31.5f,31.0f,0.f) });
pointMassElements.push_back({ 993.0f, Vector3(28.f,30.5f,0.f) });
Vector3 centerOfGravity = GetCenterOfGravity();
std::cout << "Center of Gravity: (" << centerOfGravity._x << ", " << centerOfGravity._y << ", " << centerOfGravity._z << ")\n";
for (const auto& pointMass : pointMassElements) {
std::cout << "Relative Position: (" << pointMass.relativePosition._x << ", " << pointMass.relativePosition._y << ", " << pointMass.relativePosition._z << ")\n";
}
Matrix3x3 matrix = GetInteria();
matrix.PrintMatrix();
return 0;
}
관성 텐서의 회전축은 리지드바디의 최종 무게중심을 통과한다. 따라서, 축전송 공식을 사용할 때, 반드시 각 요소에 올바른 좌표 (최종 무게중심에 대한 상대좌표)를 사용해야 한다.
위의 연산은 로컬좌표(물체에 고정된 좌표)를 사용하여 관성텐서를 계산한다.
이 장의 앞 부분에서 말했듯이 로컬좌표를 이용하여 각운동방정식을 다시 쓰고 로컬 관성텐서를 이용하면 계산량이 줄어든다.
4. 상대론적 시간
알베르트 아인슈타인은 시간의 속도는 일정하다는 통념과는 달리, 빛의 속력이 광원의 움직임과 상관없이 항상 일정하다고 주장하였다.
상대론적 시간은 시간의 흐름이 관찰자와 대상의 상대적 운동 상태에 따라 다르게 경험되는 현상을 뜻한다.
일상 경험에서 모든 시계가 동일한 속도로 움직인다고 생각하지만, 특수 상대성 이론에 따르면 이는 사실이 아니다. 이 이론의 핵심은 빛의 속도가 모든 관찰자에게 일정하다는 것이다.
진공상태에서 레이저를 쏜다고 생각해보자. 이 빛은 언제나 광속 c (299,972,458 m/s)의 속도로 이동할 것이다.
이제 우리기 0.5c 로 비행 중인 로켓의 머리 부분에서 이 레이저를 쏜다고 해보자.
그러면 당연하게도 빛의 속도는 1.5c가 되어야 할 것이다. 그러나 여기서 나오는 빛의 속도는 여전히 c이다.
아인슈타인의 특수상대성이론이 완성되어감에 따라, 이 가설은 "시공간연속체 내에서 정보를 전송할 수 있는 최대속도가 존재한다." 라는 표현으로 발전했다. 이것을 국소성의 원리라고 한다.
이 이론에서 얻을 수 있는 가장 놀라운 결론은 시간이 더 이상 절대적이지 않다는 점이다.
어떤 상황에서도 빛의 속력이 동일하려면, 속도가 증가함에 따라 시간이 감소해야만 한다.
그럼 예를 하나 들어보자. 보통과는 조금 다른 가상의 시계가 하나 있다.
이 시계는 2개의 거울과 그 사이에서 반사되는 광선으로 구성되어 있다.
이 광선이 두 거울 사이를 왕복하는 데 걸리는 시간을 틱이라고 하겠다.
그럼 틱을 다음과 같이 계산할 수 있다.
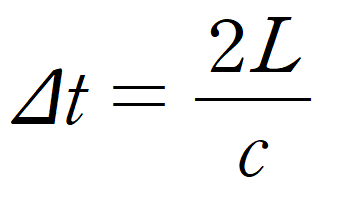
여기서 L은 두 거울 사이의 거리이고, c는 빛의 속력이다.
이제, 이 시계가 공간 속을 이동한다고 하자.
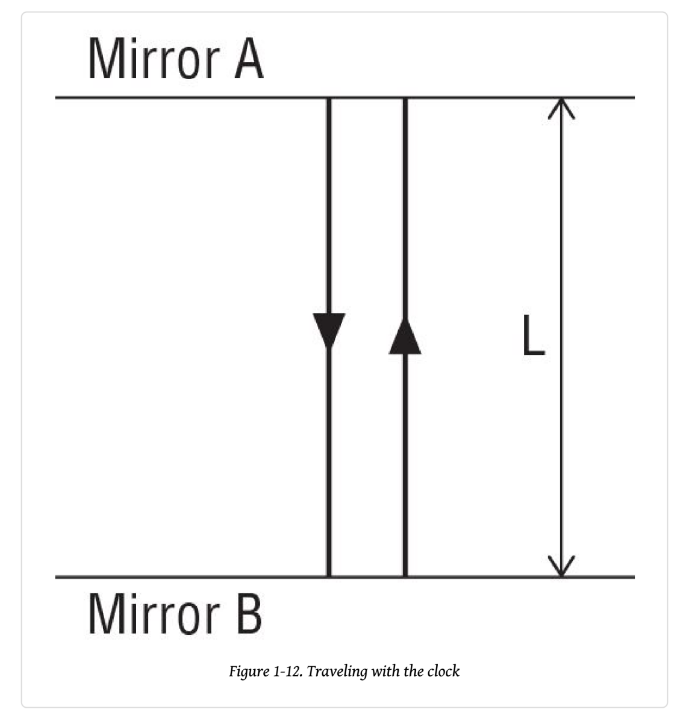

그렇다면 빛의 움직임을 보면 위 그림과 같을 것이다.
여기서 빛의 움직임을 삼각형으로 나타냈을 때,
빗변을 H, 두 거울사이의 거리를 L 이라고 하자.
그러면 두 거울 사이의 왕복거리를 왕복에 걸린 시간으로 나눈 것을 빛의 속도라고 정의할 수 있을 것이다.
빛의 속도를 c라고 했을 때, c는 다음과 같이 정의된다.
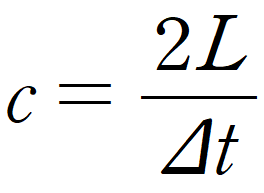
하지만, 국소성의 원리에 따르면 빛의 속도는 그 어떤 경우에도 동일해야 하므로 다음의 식도 유효하다.
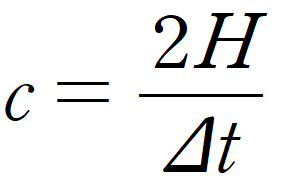
원래는 말이 안되는 식이지만 국소성의 원리에 따르면 두 식을 동치여야 한다.
동치여야 하기에 두 식의 시간 변화량은 다른 값을 가져야 한다.
이것이 의미하는 바는 다음과 같다.
고속비행 중인 로켓이 눈 앞을 지나갈 떄, 그 로켓의 안쪽 벽에 걸린 시계를 본다면 느리게 도는 게 보일 것이다.
이때 로켓 안에 있는 사람이 밖에 있는 시계를 본다면 역시 밖의 시계는 느리게 가는 것처럼 보일 것이다.
이것을 시간 지연 현상이라고 한다.
로렌츠 변환에 의하면 속도 v가 팽창하는 양은 다음과 같다.
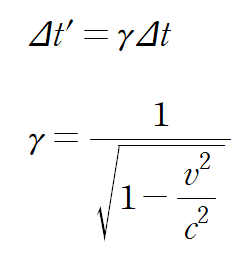
여기서 감마는 로렌츠 인자라고 부르는 것이다.
속도가 광속에 가까워짐에 따라 시간팽창의 효과가 증가한다.
일란성 쌍둥이가 한 쌍 있다고 가정하자.
동생이 광속의 75% 속도로 비행 중인 우주선에 탑승하여 지구를 떠난 뒤, 본인의 시간으로 20년 후에 지구에 돌아온다면
우리는 이미 30년이나 더 늙어 있을 것이다.
이것이 시간팽창의 효과이다. 로켓을 탄 쌍둥이의 시간이 더 느리게 흘렀기에 이런 현상이 발생한다.
상대속도에 의한 시간팽창 외에도 시간의 흐름이 느려지는 경우가 있다.
아인슈타인의 일반상대성이론에 의하면 강한 중력의 영향을 받아도 시간이 느려진다.
중력에 의한 시간팽창은 상대적이지 않다.
영희가 철수보다 블랙홀에 가까이 있다면, 누가 보기에도 영희의 시간이 더 느리게 움직일 것이다.
시간팽창의 게임은 게임 속에서 시간의 흐름을 제어할 수 있는 능력의 이론적 근거로 사용할 수 있다.
게임 속 주인공이 임무 수행을 위해 가까운 미래로 여행해야 한다면, 원심분리기에 들어가서 광속에 가까운 가속을 받는다.
이제 원심분리기에서 나오면 미래로 시간여행을 한 거나 다름이 없게 된다.
(물론 이런 시간여행은 편도여행이다.)
시간팽창의 개념은 이론적인 것만이 아닌게 이미 실생활에서 사용하고 있고 대표적인 예시가 GPS이다.
인공위성은 고속으로 공전중이기 때문에 인공위성 안의 시간은 지구의 시간보다 느리다.
그래서 GPS는 시간 지연을 고려하여 정확한 위치를 계산한다.
상대성이론에서 얻을 수 있는 또 다른 결론은 '물체가 빛보다 빠르게 이동할 수 없다.'이다.
물체의 이동속도 v가 빛의 속도 c와 같아지면 로렌츠 인자의 분모가 0이 되어버리기 때문이다.