개발하는 리프터 꽃게맨입니다.
[수학] 행렬: 가상 세계의 변환 도구 본문
1. 선형성: 예측 가능한 비례 관계

원점을 지나는 임의의 직선을 생각해보자.
이러한 직선은 선형성이라는 성질을 가진다.
수학에서는 선형성을 다음과 같은 가법성과 1차 동차성 두 가지 조건을 모두 만족하는 함수의 성질로 정의한다.
(1) 가법성

(2) 동차성

[1] 선형 함수
입력에 사용하는 요소 x와 출력이 모두 실수인 함수에서 원점을 지나는, 다음과 같은 직선의 함수를 생각할 수 있다.

출력의 원소를 y라고 표시했을 때 위 함수는 y = ax로 표현되며, 이를 그래프로 나타내면 위 그림과 같다.
이러한 직성 형태를 띠는 이 함수가 선형성을 만족하는지 확인해보자.
(1) 가법성을 만족하는가?
f(x1 + x2) = f(x1) + f(x2) 가 동일한지 확인해보자.
f(x1 + x2) = ax1 + ax2
f(x1) + f(x2) = ax1 + ax2
이므로 위 직선의 방정식은 가법성을 만족한다.
(2) 1차 동차성을 만족하는가?
f(kx) = kf(x) 가 동일한지 확인해보자.
f(kx) = akx
kf(x) = kax
이므로 위 직선의 방정식은 1차 동차성을 만족한다.
그러므로 함수 y = ax 는 선형성을 만족한다는 사실을 알 수 있다.
그렇다면 f(x) = x² 과 같은 함수는 선형성을 만족할까?
(1) 가법성을 만족하는가?
f(x1 + x2) = (x1 + x2)²
f(x1) + f(x2) = x1² + x2²
이므로 가법성을 만족하지 못한다.
(2) 1차 동차성을 만족하는가?
f(ax) = ax²
af(x) = ax²
이므로 1차 동차성을 만족한다.
이차함수는 가법성을 만족하지 못하므로 선형성을 만족하는 함수가 아님을 확인할 수 있다.
그러면 f(x) = ax + b는 어떨까?
이 함수는 가법성과 동차성 모두 만족하지 못하기 때문에 선형성을 만족하는 함수가 아니다.
이로써 선형성을 가지는 함수는
먼저, 곧게 뻗은 직성의 성질을 가져야하고
더하여 두 집합의 순수한 비(ratio)로 구성된 1차적 대응 관계를 의미한다고 볼 수 있다.
함수 f(x) = ax에서 대응되는 두 집합은 순수한 비로 구성되어 있기 때문에 다른 입력값을 투여했을 떄
어떤 출력값이 나올지 쉽게 예측할 수 있르며, 역함수 f(x)'를 사용하여 출력값을 입력값으로 거꾸로 계산하는 것이 가능하다.
[2] 벡터 공간의 선형 변환
이제 2차원 벡터 공간으로 설정한 상황에서 선형성을 가지는 함수에 대해 알아보자.
정의역에 해당하는 벡터 공간을 V, 그 원소를 v로, 공역에 해당하는 벡터 공간을 W, 그 원소를 w로 표시해보겠다.
2차원 벡터를 입력받고 2차원 벡터를 출력하는 함수 f가 있을 때
선형성을 가지는 함수를 설계해보겠다.
입력에 사용한 2차원 벡터가 (x, y) 로 구성되어 있는 경우 x와 y는 독립적으로 계산이 가능하다.
(서로 영향을 미치지 못한다.)
앞서 선형 함수는 직선 함수 + 순수한 비의 형태를 띈다는 것을 확인했고
따라서 x와 y에 각각 선형성을 유지하고자 한다면 이들은 ax와 by 같은 단순 비의 형태를 사용할 것이고,
이를 섞은 최종결과는 ax + by 의 형태가 될 것이다.
따라서 2차원 벡터를 입출력으로 사용하는 선형성을 가지는 함수는 다음과 같이 설계할 수 있다.
f(v) = f(x, y) = (ax + by, cx + dy)
위 함수가 가법성과 동차성을 만족하는지 한 번 알아보자.
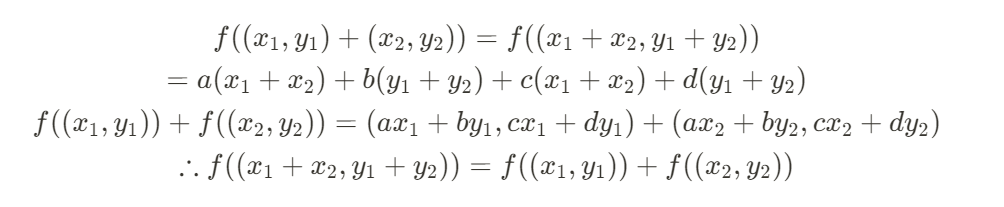
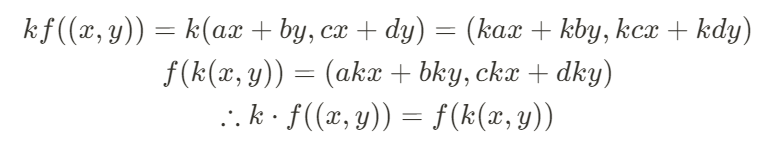
그러므로
f(x, y) = (ax + by, cx + dy) 는 선형 함수임을 확인할 수 있다.
표준기저벡터의 선형 결합으로 형성된 벡터 공간은 선형성을 지닌다.
이 벡터 공간을 선형 함수로 변화시킨 새로운 공간도 기저벡터의 선형 결합으로 형성되므로 선형성을 지닌다.
이렇게 두 공간이 동일한 구조를 지닐 때 두 공간의 대응 관계를 변환이라고도 부른다.
따라서 선형성을 유지시켜주는 선형 함수 f(x, y) = (ax + by, cx + dy) 는 선형 변환이다.
벡터 공간에서 발생하는 선형 변환의 원리는 크기 변환이나 회전 변환과 관련이 있다.
임의의 벡터 v(x, y) 의 크기를 k배 늘리는 작업은 다음과 같이 스칼라 곱셈으로 표현이 가능했다.
f(v) = f(x, y) = (kx, ky)
이는 (ax + by, cx + dy) 에서 a = k, b = 0, c = 0, d = k 를 대입한 결과와 동일하므로 선형 변환임을 알 수 있다.
앞에서 살펴본 회전 변환에 대하여 함수로 표현하면 다음과 같다.
f(v) = (x, y) = (cos θ x - sin θ y, sin θ x + cos θ y)
이 역시 (ax + by, cx + dy) 형식에서 a, b, c, d 에 적절한 값을 대입한 것일 뿐이므로
선형 변환이라고 할 수 있다.
벡터 공간에서의 선형 변환은 앞서 살펴본 단순한 비례 관계로 구성된 선형 함수 f(x) = ax 처럼 두 집합의 순수한 비를 통해 예측할 수 있는 형태로 변환되며, 역함수를 통해 변환 후의 벡터로부터 변환 전의 벡터를 파악할 수 있다.
수학자들은 선형 변환의 계산 과정을 체계화하여 손쉽게 계산할 수 있는 편리한 도구를 발명했는데,
그것이 바로 다음에 설명할 행렬이다.
2. 행렬
행렬은 수를 사각형의 형태로 행과 열을 맞춰 배열한 테이블이다.
따라서 n개의 행과 m개의 열고 구성된 반듯한 사각형의 형태를 띤다.
예를 들어 2x3 행렬은 다음과 같이 2행 3열의 형태를 띤다.
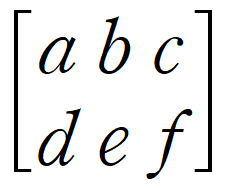
행렬은 선형 변환과 벡터를 나타내는 데 사용된다.
벡터는 한 줄로 구성된 행렬로 표현되며, 가로와 세로 두 가지 표현 방식이 존재한다.
(x, y) 로 구성된 2차원의 벡터는 다음과 같은 행렬로 표기할 수 있는데, A는 열벡터, B는 행벡터라고 부른다.
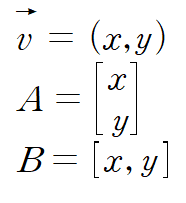
선형 변환을 표현할 때는 행과 열이 크기가 같은 정방행렬을 사용한다.
서 살펴본 2차원 벡터 공간의 선형 변환 f(x, y) = (ax + by, cx + dy) 는 2 x 2 크기의 정방행렬로 표현하느넫,
이에 대응하는 행렬 A는 다음과 같다.
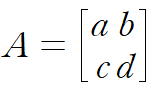
정방행렬 A는 2개의 행벡터 또는 2개의 열벡터로 구성된다고 할 수 있다.
[1] 행렬의 기본 연산
행렬은 사각형의 형태로 수를 배열한 것에 불과하지만 지정된 계산 방법을 통해 많은 문제를 해결할 수 있다.
일반적으로 사용되는 행렬의 연산에 대해서 알아보자.
(1) 행렬과 행렬의 덧셈
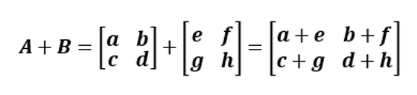
행렬과 행렬의 덧셈은 행렬의 크기가 같은 경우에만 성립된다.
위치가 같은 원소끼리 덧셈을 수행한다.
(2) 행렬과 스칼라의 곱셈
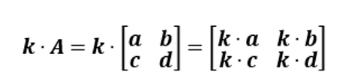
행렬에 스칼라를 곱하는 연산은 다음과 같이 행렬을 구성하는 모든 원소에 스칼라를 곱한다.
(3) 행렬의 전치 (transpose of a matrix)
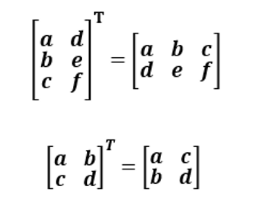
전치연산은 첨자 T로 표시하는데 행과 열을 바꾸는 작업을 수행한다.
그러면 3x2 행렬은 전치연산 후 2x3 행렬이 된다.
행과 열의 크기가 같은 정방행렬의 전치연산은 행과 열의 정보가 동일한 대각 성분의 원소는 그대로 유지되고
나머지 원소는 대각 성분을 중심으로 대칭된 행렬을 만든다.
(4) 행렬과 행렬의 곱셈 (행렬 곱)
두 행렬 A, B에 대해서 행렬 곱을 수행한다고 하면
AㆍB 와 같이 표기하며, 행렬 A의 행벡터와 행렬 B의 열벡터를 각각 곱하는 방식으로 진행된다.
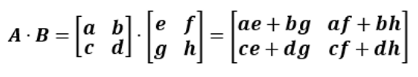
행렬 곱셈의 중요한 성질 중 하나는 교환법칙이 성립하지 않는다는 점이다.
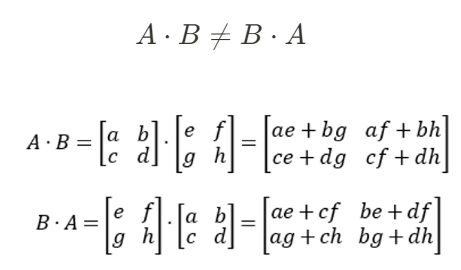
한편, 다음과 같이 결합법칙을 만족한다.
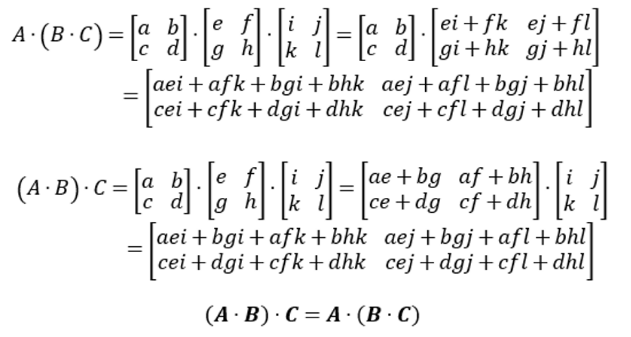
행렬 곱의 특징 중 하나는, 행렬 곱을 전치한 결과는 순서를 바꾼 후 각각 전치해 곱한 결과와 동일하다는 것이다.
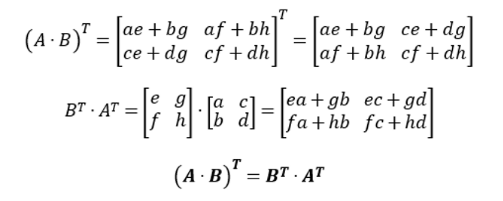
a, b, c, d 4개의 원소로 구성된 2x2 정방행렬과 2차원 벡터 (x, y)를 열벡터로 설정한 두 행렬의 곱은 다음과 같이 전개된다.
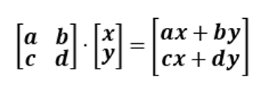
행렬 곱의 결과는 앞서 살펴본 2차원 벡터 공간의 선형 변환 f(x, y) = (ax + by, cx + dy) 와 동일하다.
따라서 2 x 2 정방행렬 A는 2차원 공간의 선형 변환에 대응되는 함수를 의미하고,
이 수식은 f(x, y) = (ax + by, cx + dy) 2차원 벡터에 선형 변환을 적용해 새로운 벡터를 생성하는 작업으로 해석할 수 있다.
또한, 선형 변환을 적용하기 위한 연순 순서는 오른쪽에서 왼쪽 방향으로 이뤄짐을 알 수 있다.
<주의할 점>
행렬 A, B 를 행렬 곱할 때
A의 열 수는, B의 행 수와 동일해야한다.
[2] 정방행렬의 곱셈
2 x 2 정방행렬과 벡터의 곱이 2차원 벡터 공간의 선형 변환에 대응된다면
2 x 2 정방행렬 간의 곱은 앞서 다룬 합성함수에 대응되는 연산이다.
벡터 V에 선형 변환을 나타내느 2X2 정방행렬 A, B를 순서대로 연산한다고 생각해보자.
연산 순서는 오른쪽에서 왼쪽으로 진행되므로 이의 수식은 다음과 같다.
w = BㆍAㆍv
벡터 v와 행렬 A, B 를 다음과 같이 나타낼 수 있을 떄
새로운 벡터 w를 만들어 보자.
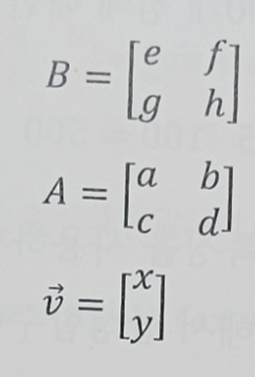
라고 할 때
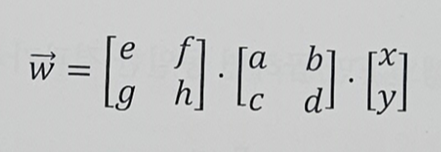
이런 식의 행렬 곱으로 표현할 수 있다.
그런데 앞서 합성함수는 결합법칙을 만족한다고 언급했는데,
합성함수에 대응하는 행렬의 곱셈 역시 결합법칙을 만족한다.
따라서 행렬의 연산 순서를 바꿔도 최종 계산된 벡터 w의 값은 동일하다.
w = (BㆍA) v = Bㆍ(Aㆍv)
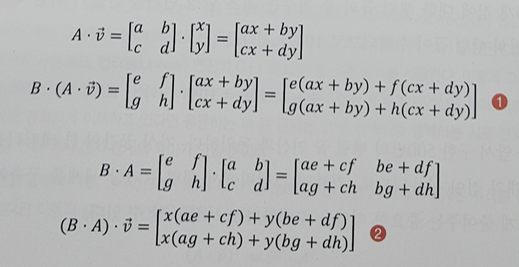
그러므로 이러한 식을 찾을 수 있다.
이처럼 결합법칙이 성립하는 행렬 곱의 성질은 컴퓨터 그래픽 연산에서 아주 유용하게 활용된다.
예를 들어 100개의 점으로 구서오딘 물체가 모니터에 표현되기까지 5번의 선형 변환이 발생한다고 가정해보자.
각각의 선형 변환 행렬을 A, B, C, D, E 라고 하자
그러면
EㆍDㆍCㆍBㆍAㆍ v1
EㆍDㆍCㆍBㆍAㆍ v2
.
.
.
EㆍDㆍCㆍBㆍAㆍ v99
EㆍDㆍCㆍBㆍAㆍ v100
각 점마다 5번의 행렬 곱이 수행되므로 100개 점에 대한 행렬 곱의 총 횟수는 500이 될 것이다.
이때 결합법칙이 성립하는 행렬 연산의 특징을 사용하면 계산량을 줄이되 동일한 결과를 얻을 수 있다.
다음과 같이 행렬 곱을 4번 수행해서 합성함수에 해당하는 행렬 F를 미리 만들어두자.
F = EㆍDㆍCㆍBㆍA
이제 각 점에 대해 미리 계산된 행렬 F만 곱하면 동일한 결과가 나온다.
Fㆍ v1
Fㆍ v2
...
Fㆍ v99
Fㆍ v100
이 경우 100개에 점에 대한 행렬 곱의 총 횟수는 100 + 4 = 104가 된다.
이 결과는 앞서 구한 500번의 행렬 곱 연산과 동일하다.
가상 공간의 한 캐릭터를 표현하는 데 보통 10만 개의 점이 사용되므로,
컴퓨터 그래픽에서 행렬은 가상 세계를 구축하는 데 필요한 계산량을 크게 줄여주는 중요한 역할을 수행한다는 사실을 알 수 있다.
[3] 열 기준 행렬과 행 기준 행렬
행렬과 벡터의 곱셈을 수행하는 방식으로 ,열 기준 행렬과 행 기준 행렬 2가지가 있다.
수학에서 행렬을 다룰 때는, 벡터를 열벡터로 나타내는 열 기준 행렬 방식을 주로 사용한다.
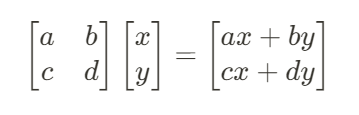
그런데 컴퓨터에서 실제로 행렬을 응용할 때는, 행 기준 행렬을 사용하는 경우도 있다.
행 기준으로 선형 변환을 수행할 떄는 열 기준과 다르게 행렬과 벡터의 위치를 거꾸러 뒤집어서
벡터ㆍ행렬 순으로 계산한다.
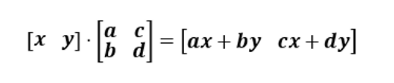
한 정방행렬 A
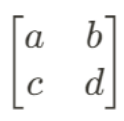
가 존재한다고 할 때,
열 방향 벡터를 v1, 행 방항 벡터를 v2 라고 하자
Aㆍv1 와
v2ㆍA 는 서로 다른 x, y 값을 가진다.
즉, 계산 순서만 바꿔서는 열 방향 벡터와 행 방향 벡터는 동일한 값을 가지지 않는 다는 의미이다.
Aㆍv1 의 결과와 동일한 행 방향 벡터 계산을 하기 위해선
A의 전치행렬을 사용해야만 한다.
그 풀이를 아래 따로 첨부하겠다.
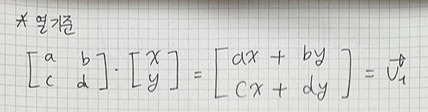
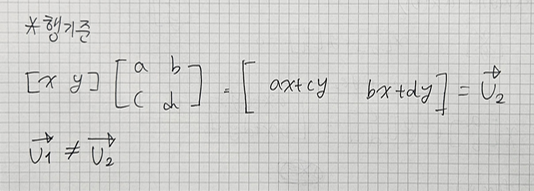
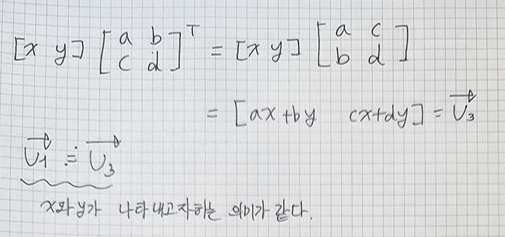
그러므로 열 기준 체계에서 설계된 수식을 행 기준에서 가져다 쓰고 싶다면 그 전치연산을 적용해 변환하기만 하면 된다.
행 기준 체계를 사용하는 사례로는 DirectX, Unreal 엔진이 있으며
열 기준 체계를 사용하는 사례로는 OpenGL, Unity 엔진이 있다.
그래픽 라이브러리와 응용마다 행렬을 사용하는 방법은 다르지만, 두 방식 모두 전치연산을 통해 서로 변환할 수 있으므로 방식만 명확하게 이해하고 있다면 응용하는 데 큰 문제는 없다.
열벡터와 행벡터는 서로 전치 관계에 있기 때문에, 선형 변환 역시 전치 관계의 차이가 있을 뿐이다.

열 기준 행렬은 행렬의 전용 순서가 오른쪽에서 왼쪽 방향으로 흐르는 역방향으로 진행된다,
다음 행렬의 곱셈이 열 시준 방식으로 이뤄진다면, 벡터 v에 대해 행렬 A의 선형 변환이 적용된 후 행렬 B의 선형 변환이 적용된다.
BㆍAㆍv = w
그러나 전치하여 행 기준 방식으로 변환해보자
그러면 다음과 같이 식이 전치된다.
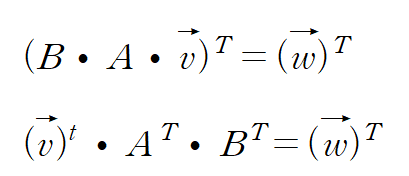
이와 같이 열 기준 방식을 전치하여 행 기준 벡터로 변환 했다면
행렬의 적용 순서는 왼쪽에서 오른쪽의 순방향으로 진행되므로 이 점을 주의하자.
3. 행렬의 설계
지금까지 2x2 정방행렬이 2차원 벡터 공간의 선형 변환에 대응한다는 점을 확인했다.
이번에는 평면상의 물체를 우리가 원하는 형태로 변환하기 위해 2x2 행렬을 설계하는 방법에 대해 살펴보겠다.
벡터 공간 V를 구성하는 두 표준기저벡터 (1, 0) 과 (0, 1) 이 선형 변환을 통해
새로운 벡터 공간 W의 벡터 (a, c)와 (b, d)에 대응되어 변환된다고 생각해보자.
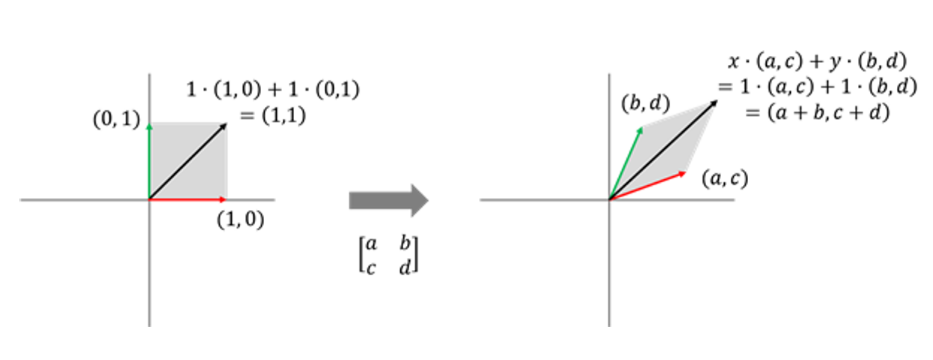
원 벡터 공간에서
임의의 벡터 v = (x, y) 는
표준 기저 벡터와의 선형 결합을 통해 생성되었다.
이를 식으로 나타내면 다음과 같다.
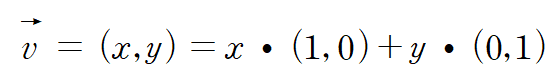
벡터 v가 선형 변환되는 경우에는 동일한 선형 결합식을 사용해 벡터 w가 다음과 같이 계산된다.
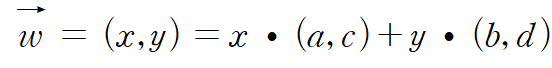
이는 a, b, c, d로 만들어진 정방행렬에 벡터 (x, y)를 곱한 결과와 동일하다.
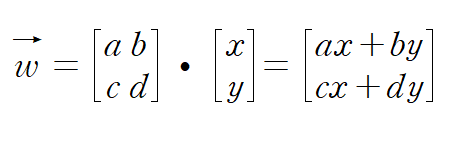
위의 정방행렬과 표준기저벡터가 변화된 두 벡터 (a, b)와 (b, d) 와의 관계를 분석해보면 이들은
정방행렬을 구성하는 열벡터임을 알 수 있다.
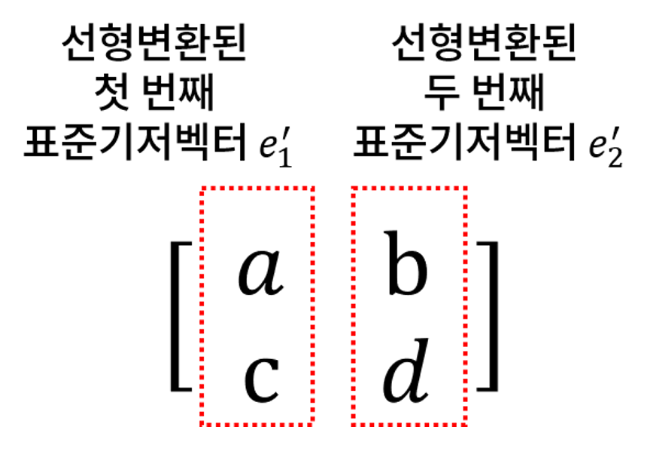
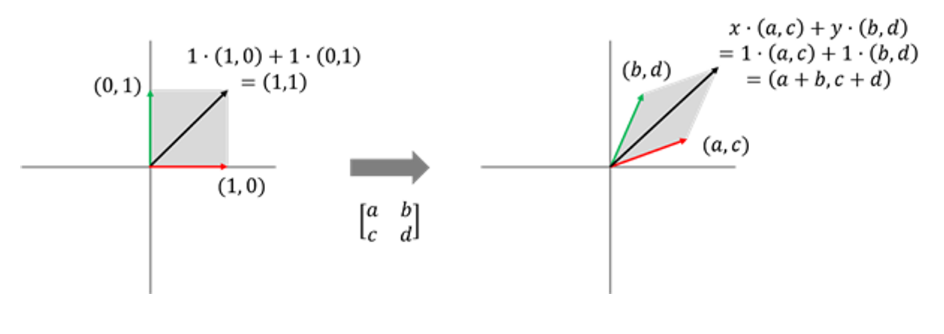
벡터 공간 V의 (0, 0)에서 (1, 1) 까지로 둘러싸인 사각형의 부분 공간을 관찰해 벡터 공간 V에서 벡터 공간 W로의 변환을 눈으로 확인해보자.
이렇게 변화를 관찰함으로써 선형 변환을 눈으로 확인할 수 있으며
이를 활용해 우리가 원하는 형태로 공간이 변환되도록 행렬을 스스로 설계할 수 있다.
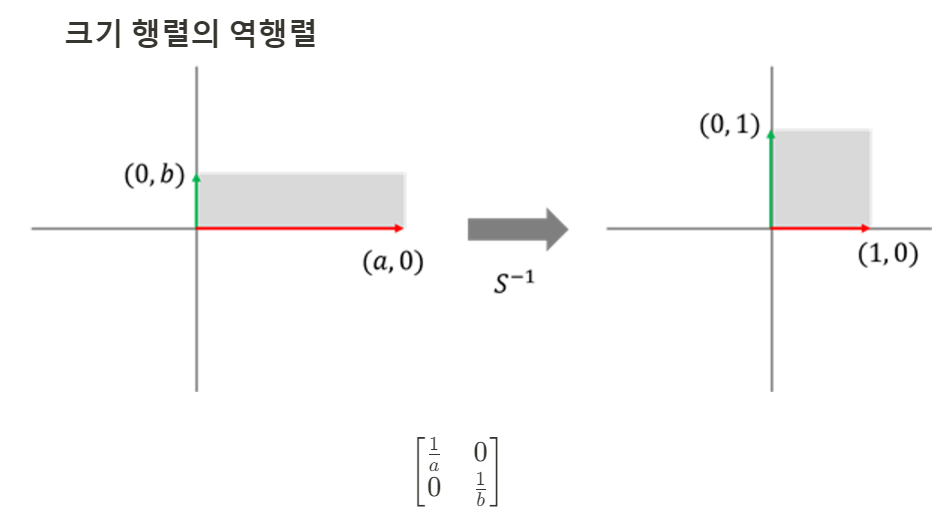
[1] 크기 변환 행렬
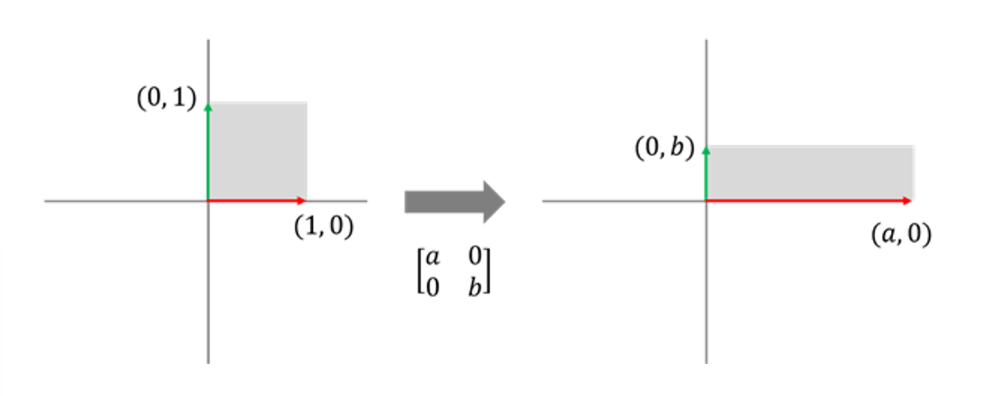
크기 변환행렬은 물체의 크기를 변경하는 행렬이다.
크기 변환은 각 표준기저벡터를 동일한 방향으로 지정한 크기만큼 늘리는 변환을 의미한다.
표준기저벡터 e1을 a배 늘리거나 줄인 벡터 e1' = a * (1, 0) = (a, 0)
표준기저벡터 e2를 b배 늘리거나 줄인 벡터 e2` = b * (0, 1) = (0, b)
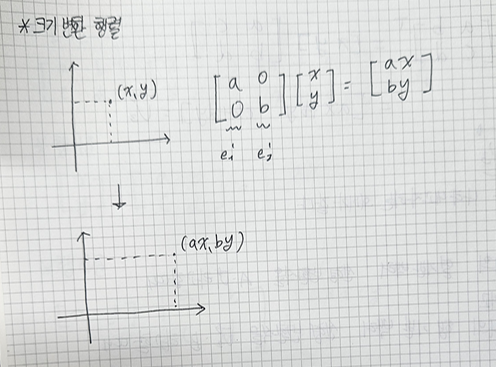
[2] 회전 변환 행렬
주어진 각 θ로 벡터 공간을 회전시키는 회전 변환행렬을 설계해보자.
먼저 90' 변환 행렬부터 살펴보자
먼저 양의 방향으로 (반시계방향) 회전시켜보겠다.
앞서 살펴본 회전 식를 생각해보면 표준기저벡터는 다음과 같은 식을 가진다.
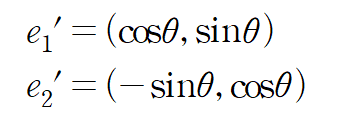
그러므로
θ = 90 일 경우
e1 = (0, 1)
e2 = (-1, 0)
이다.
이를 통해 변환 행렬을 설계하면 다음과 같다.
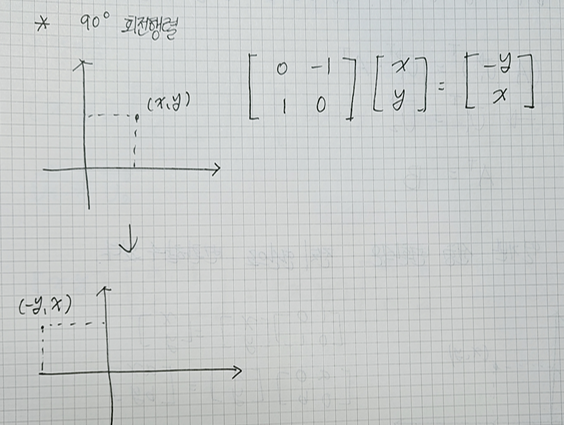
시계 방향으로 90' 회전시키는 변환 행렬은
e1 = (0, -1)
e2 = (1, 0)
로 변환을 수행하면 된다.
사실 90' 회전 변환 행렬은 x, y 값과 부호를 바꾸는 것 만으로도 간단히 구현할 수 있다.
그렇다면 주어진 각 θ로 벡터 공간을 회전시키는 회전 변환 행렬에 대해서 알아보자.
앞서 말했듯
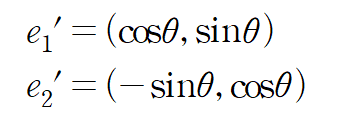
θ 만큼 회전시킨 표준기저벡터는 위와같은 결과를 가진다.
그러므로
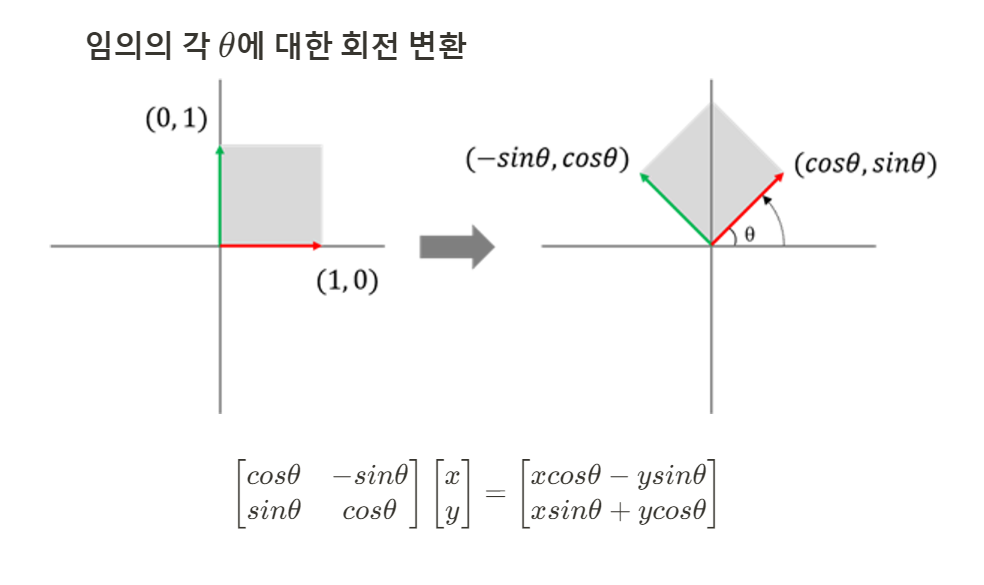
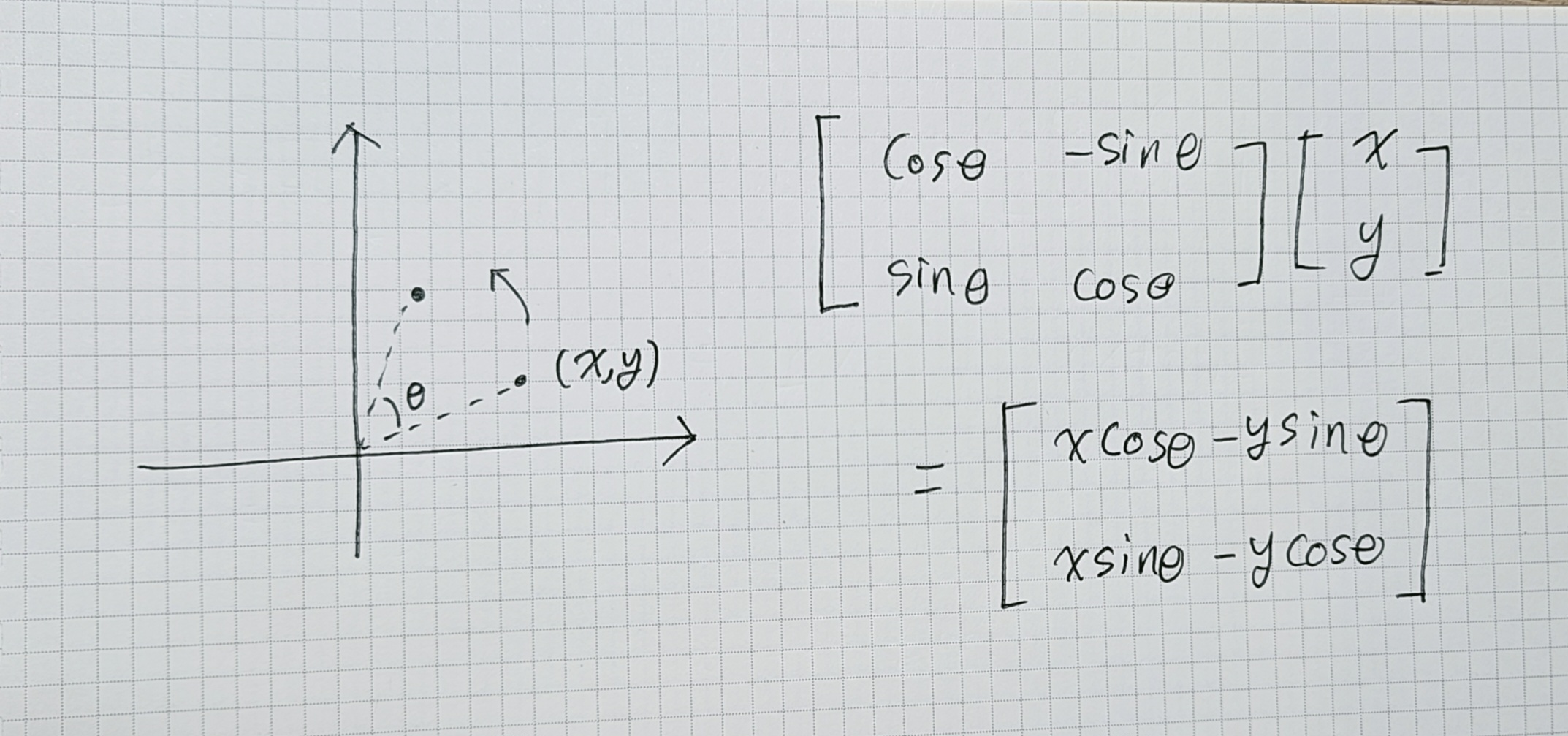
이러한 변환행렬을 얻을 수 있다.
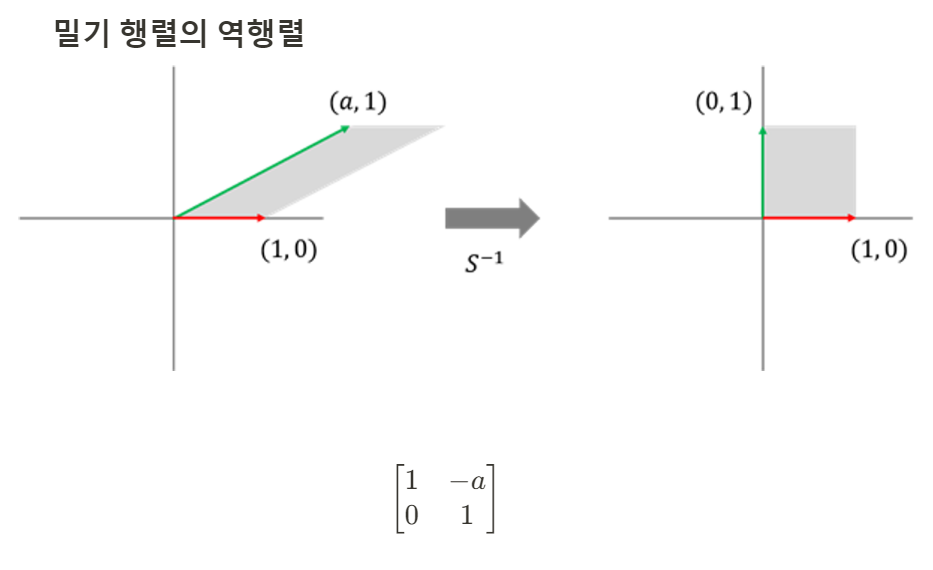
[3] 전단 변환 행렬
이번에는 표준기저벡터 e1을 고정한 상태에서 표준기저벡터 e2를 x축 방향으로 미는 변환을 생각해보자.
표준기저벡터 e1은 고정되어 있기 떄문에 변환된 결과는 아래 그림과 같이 대각선으로 밀리는 형태를 띤다.
이를 '전단 변환행렬' (shearing) 이라고 한다.
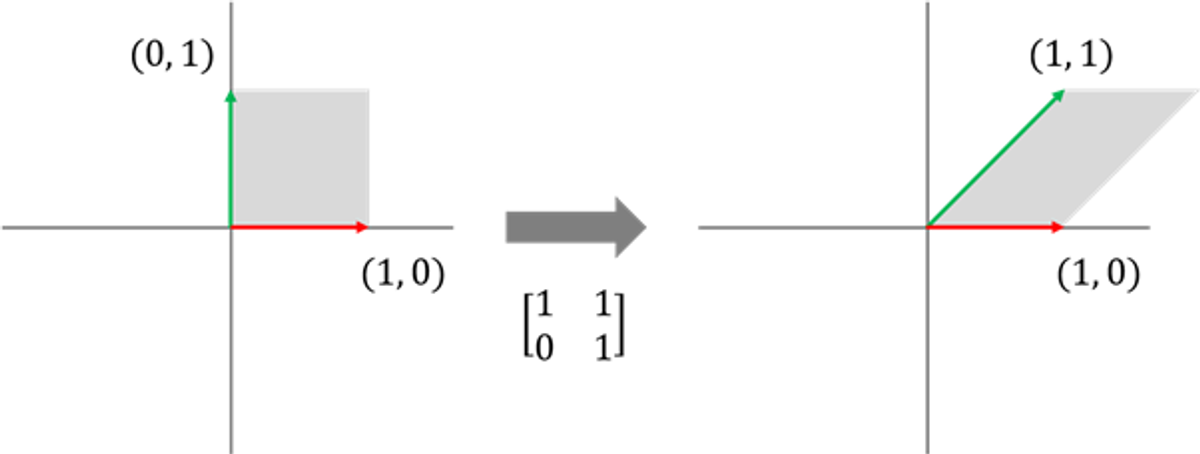
전단의 경우
한 기저벡터를 고정하고, 다른 기저벡터만 변환시켜서 전달 변환행렬을 설계할 수 있다.
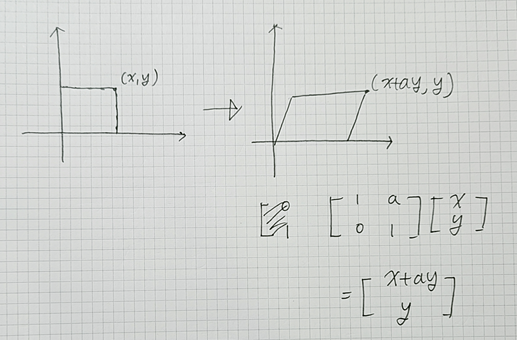
[4] 삼각함수의 덧셈 정리
삼각함수를 응용할 때 유용하게 사용되는 공식에는 삼각함수의 덧셈 정리가 있다.
cos 함수와 sin 함수의 덧셈 정리는 다음과 같다.

중고교과정에서 이 공식들을 암기했는데, 회전행렬의 원리를 잘 파악하고 있다면 행렬 곱을 사용해 덧셈 정리를 유도할 수 있다.
두 각 a와 b가 있을 때
a+b 만큼 회전한 변환은 두 각에 대한 회전 변환을 순서대로 적용한 결과와 동일하다.
즉, (a+b) 회전변환 = b 회전변환 ㆍ a 회전변환
이라는 의미이다.
유도 과정은 다음과 같다.
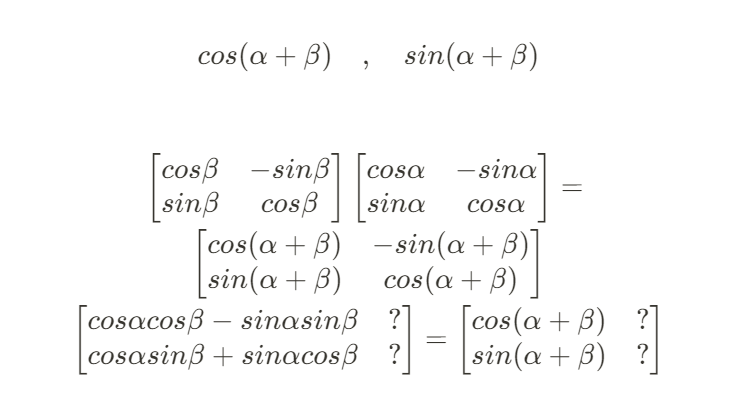
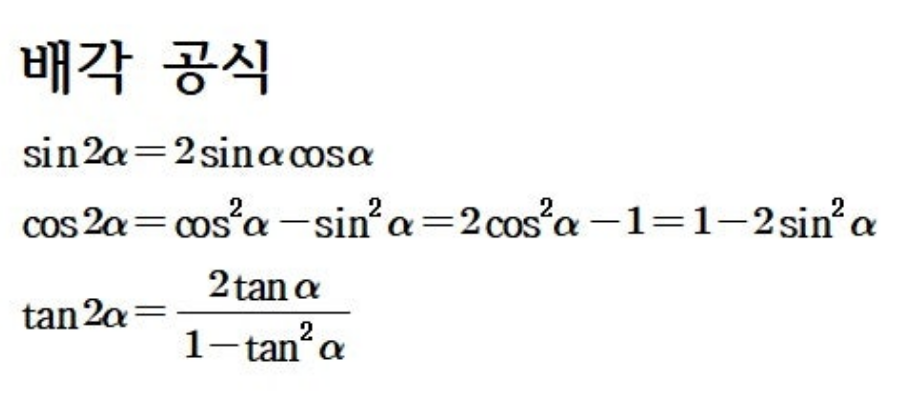
삼각함수에는 배각 공식이라는 것도 있는데
이는 삼각함수 덧셈 정리에서 두 각에 동일한 값을 삽입하면 유도할 수 있다.
4. 역행렬
선형 변환을 수행하는 행렬은 본질적으로 함수의 성질을 지니기 때문에 함등함수와 역함수에 대응하는 행렬이 존재한다.
각각을 항등행렬과 역행렬이라고 한다.
항등행렬은 원 공간의 변화없이 동일한 공간으로 유지하는 변환을 의미하며, 이는 해당 차원의 표준기저벡터와 동일하다.
항등행렬은 I 기호를 사용하여 표기한다.
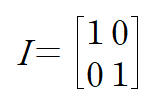
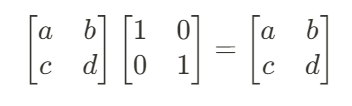
또한 역함수의 정의와 동일하게 어떤 행렬 식 A에 행렬 B를 곱을 하여 항등행렬을 만들 수 있을 때,
행렬 B를 행렬 A의 역행렬이라고 부른다.
역행렬은 역함수와 동일하게 위 첨자 -1를 사용해 표시한다.
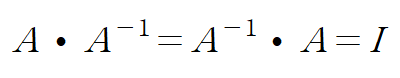
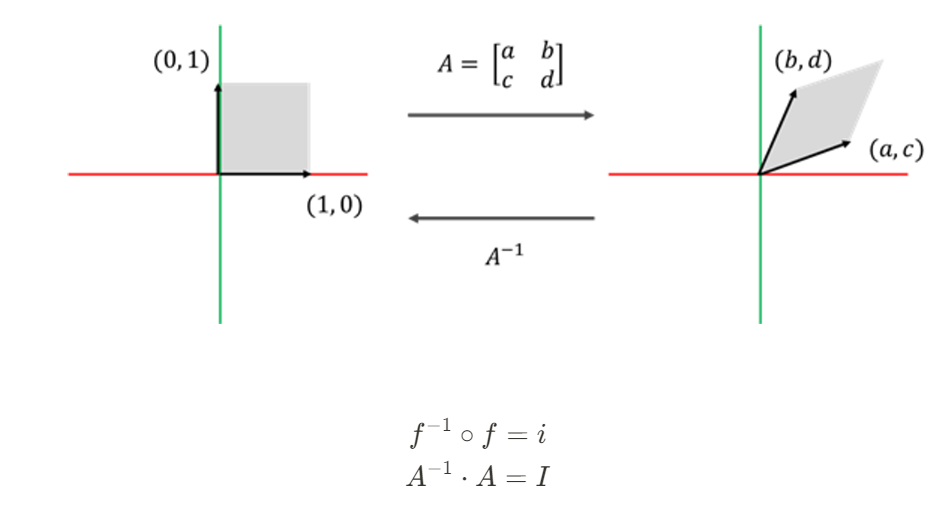
역행렬을 시각적으로 해석해본다면
역행렬은 선형변환에 의해 변환된 벡터공간을 다시 원 벡터 공간으로 되돌리는 행렬이라고 볼 수 있다.
[1] 역행렬의 존재를 판별하는 행렬식
어떤 함수가 역함수를 갖기 위해서는 반드시 '전단사함수'여야 한다.
행렬도 역시 두 공간의 변환이 전단사로 댕응될 때만 역행렬이 존재한다.
어떤 행렬에 대해 역행렬이 존재하는지 파악할 수 있는 특별한 수식이 있는 데 이를 행렬식(det, determinant)라고 한다.
행렬식은 det() 기호로 표시하며, 일반적인 2x2 정방행렬 A의 행렬식은 다음과 같이 계산한다.
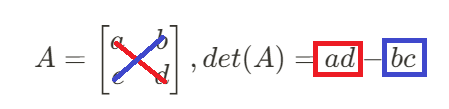
행렬식 det(A)의 값이 0인 선형 변환은 전단사 대응이 성립하지 않아 역행렬이 존재하지 않는다.
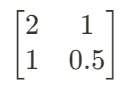
이러한 값을 가지고 있는 행렬 A가 존재한다고 하자.
원 벡터 공간 V의 두 표준기저벡터는 각각 (2, 1)과 (1, 0.5)의 열벡터로 변환됨을 알 수 있다.
변환된 두 표준기저벡터를 추적하면, 두 기저벡터의 길울기가 같음을 알 수 있다.
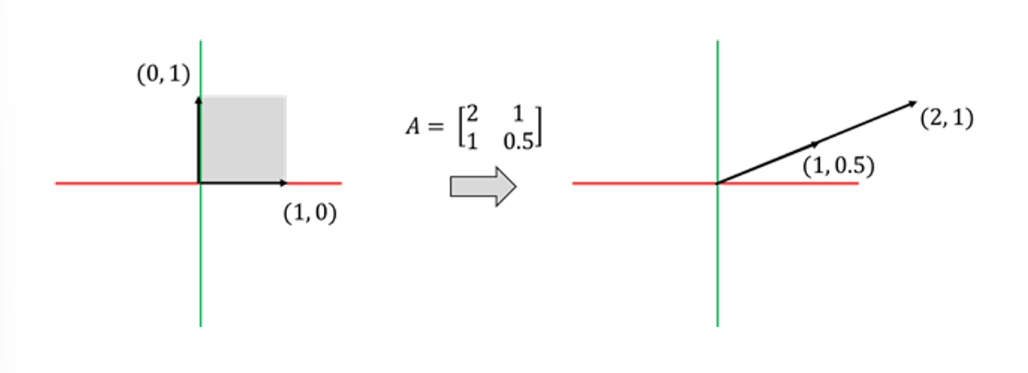
이를 시각적으로 분석하면 2차원의 평면 영역이 1차원의 직선 영역으로 압축됐다고 볼 수 있는 것이다.
이렇게 차원이 줄어들면 원 공간에 대한 정보가 소멸된다.
즉, 원 벡터 공간 V에서 벡터 공간 W로 변환을 했지만 역은 불가능하다는 의미이다.
따라서 역행렬이 존재할 수 없는 것이다.
행렬식이 0일 경우 어째서 벡터 공간의 차원이 줄어드는 것일까?
벡터 공간 V에서 임의의 행렬
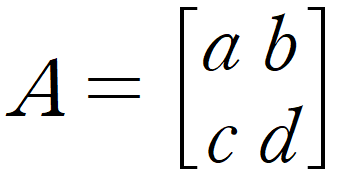
을 사용해 표준기저벡터가 (a, c)와 (b, d) 로 변환된 새로운 벡터 공간 W를 생각해보자.
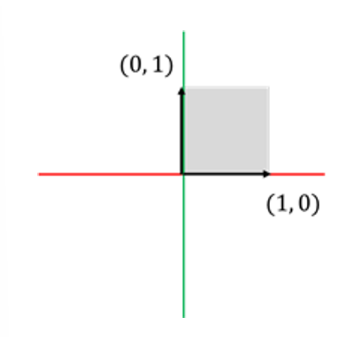
왼쪽 그림에서 회색으로 칠해진 두 표준기저벡터가 형성하는 정사각형 영역의 넓이는 1이다.
해당 영역이 행렬에 의해 평행사변형으로 변환되면 넓이도 변화될 것이다.
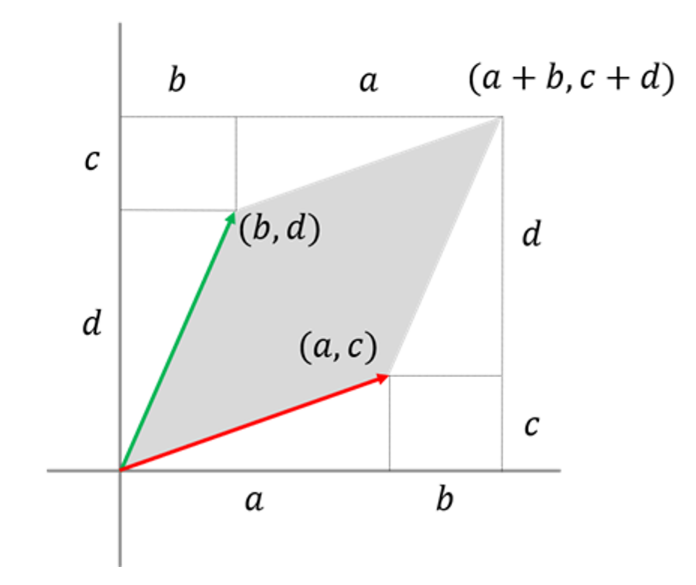
그렇다면 변환된 두 벡터가 이루는 평행사변형의 넓이는 어떻게 될까?
평행사변형의 넓이는, 전체 사각형의 넓이에서 평행사면형을 제외한 삼각형과 사각형을 빼서 구할 수 있는데
이 값은 앞에서 구한 행렬식 det(A)와 동일하다.
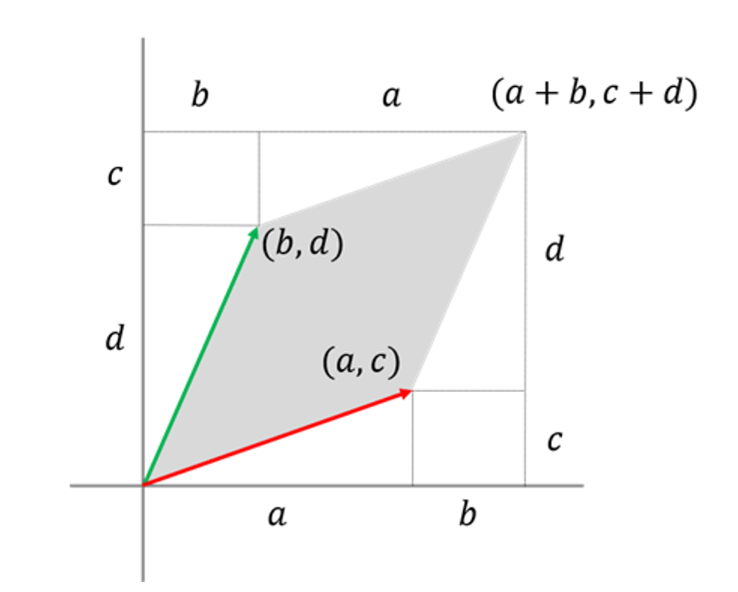
따라서 이렇게 계산된 넓이, 즉 행렬식 값이 0인 경우에는 해당 평행사변형의 넓이는 소멸되면서 평면의 모든 요소는 1차원 선 위에 놓이게 되어 이후에는 더 이상 2차원으로 돌아갈 수 없게 된다.
[2] 역행렬을 구하는 방법
역행렬은 연립방정식의 해를 구할 때 유용하게 사용된다.
만약 선형 변환 A와 변환된 벡터 v`만 알고 있는 경우 A의 역행렬을 구해 벡터 v를 구할 수도 있다.
임의의 정방행렬의 역행렬을 구하기 위한 방법으로 여러가지가 있는데 대표적으로 사용하는 방법은
가우스 소거법과 크라메르 공식이다.
(1) 가우스 소거법
임의의 행렬
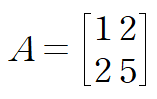
이 존재할 때
(A|I) 인 확장 행렬을 만든 다음
왼쪽 행렬을 단위 행렬로 만들면, 오른쪽 부분이 A의 역행렬이 된다.
풀이 예시는 다음과 같다.
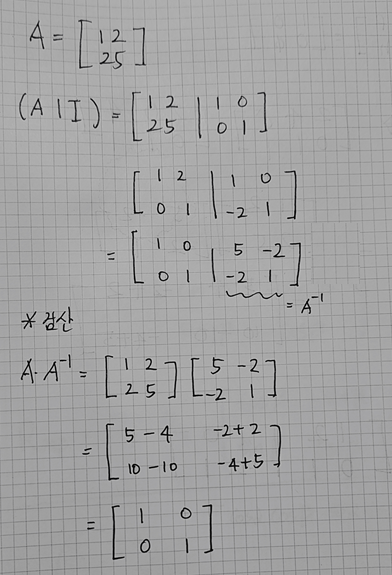
(2) 크라메르 공식
생략
[3] 자주 사용되는 변환 행렬의 역행렬
우리가 사용하는 대표적인 선형 변환들은 위의 방법을 사용하지 않고 직관적으로 역행렬을 구하는 것이 가능하다.
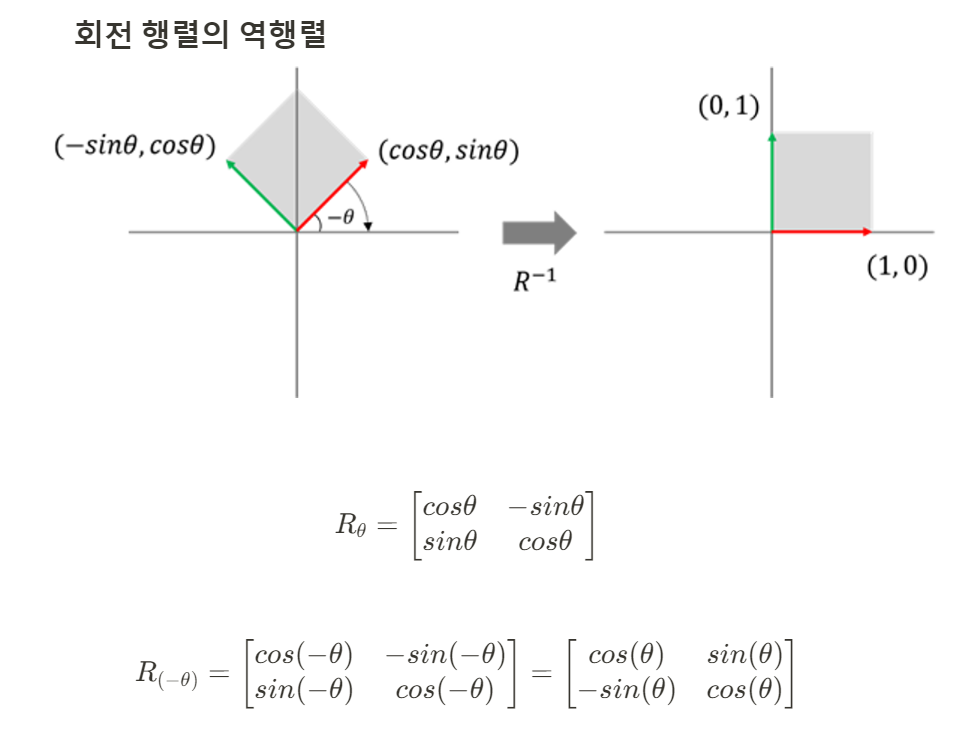
회전각 θ에 대한 회전 변환행렬의 역행렬은 반대방향의 회전각 - θ에 대한 회전 변환을 의미한다.
이를 활용하면 회전행렬의 역행렬은 위와 같이 정리할 수 있는데,원 행렬과 역행렬을 비교해보면 서로 전치 관계에 있음을 확인할 수 있다.따라서 회전행렬의 역행렬은 별도로 삼각함수를 사용하지 않아도 기존 행렬에 전치연산을 적용하는 방법으로 쉽게 구할 수 있다.
[4] 행렬 곱의 역행렬
합성함수의 역함수에 대해 다음의 수식이 성립됨을 확인했다.
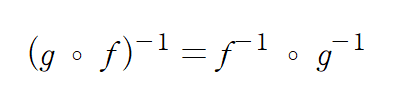
합성함수에 해당하는 두 행렬 곱의 역행렬도 동리하게 다음의 수식이 성립한다.
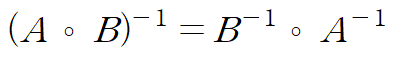
'컴퓨터 그래픽스 > 수학' 카테고리의 다른 글
| [수학] 아핀 공간: 움직이는 가상 세계의 구축 (0) | 2024.07.11 |
|---|---|
| 공부목적으로 사용할 수학 라이브러리 (0) | 2024.06.30 |
| [수학] 삼각함수: 회전을 위한 수학 (0) | 2024.06.28 |
| [수학] 벡터: 가상 공간의 탄생 (0) | 2024.06.27 |
| [수학] 수: 가상 세계를 구성하는 가장 작은 단위 (0) | 2024.06.27 |



