3D 카메라 수정

제가 사용하는 3D 카메라 입니다.
카메라의 모델링 행렬로 부터 뷰 행렬을 얻어냅니다.
뷰 행렬은 카메라 모델링 행렬의 역행렬이고, 이를 모든 오브젝트에 곱합니다.
이를 뷰 변환이라고 부릅니다.

윈도우 자체는 원점을 기준으로 그릴 것이므로
카메라의 시점을 윈도우에 그리기 위해서는, 카메라가 변환된 만큼 월드를 역변환해야 합니다.
그러면 카메라의 좌표, 회전, 크기변환 상태가 모두 원상태로 변환되며, 이에 맞추어 다른 물체들도 변환됩니다.

좌표계 설계에 따라서 다르겠지만
제가 설정한 좌표계는 양의 Z축 방향에서 바라본다고 생각하고, 렌더링을 수행합니다.
그런데 이러면 카메라의 렌즈랑 마주보는 형태죠
카메라의 형태를 생각하면, 카메라의 후면에 맺힌 영상을 보는 것이 더 직관적일 겁니다.

그래서 뷰 변환 행렬에 조금 수정을 가해야합니다.
Y축을 기준으로 180' 회전시켜줘야하죠
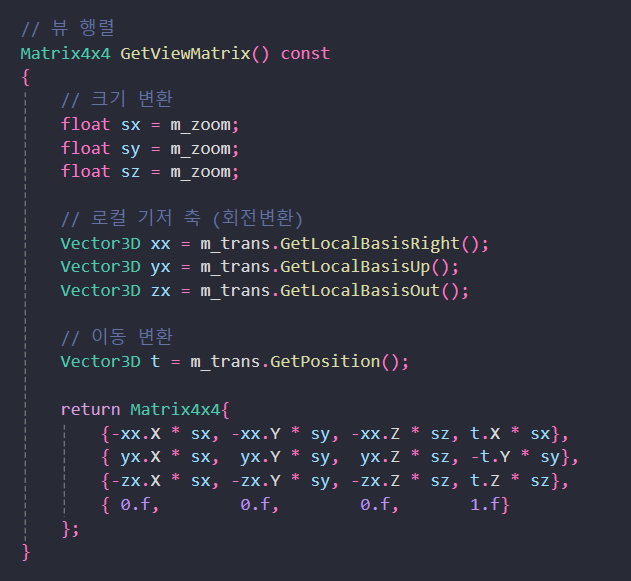
이를 구현하기 위해서 뷰 변환 행렬에서 사용되는 카메라의 Right, Out 로컬 기저축을 반전시켜주었습니다.
원근법

현재까지 만들어낸 3차원 세계입니다.
꽤나 그럴듯 해보이지만..

제가 정점 버퍼를 채울때, 좌표값에서 Z값을 완전히 소멸시켰기 때문에, 3차원 특유의 깊이감, 원근감을 주지 못하고 있습니다.
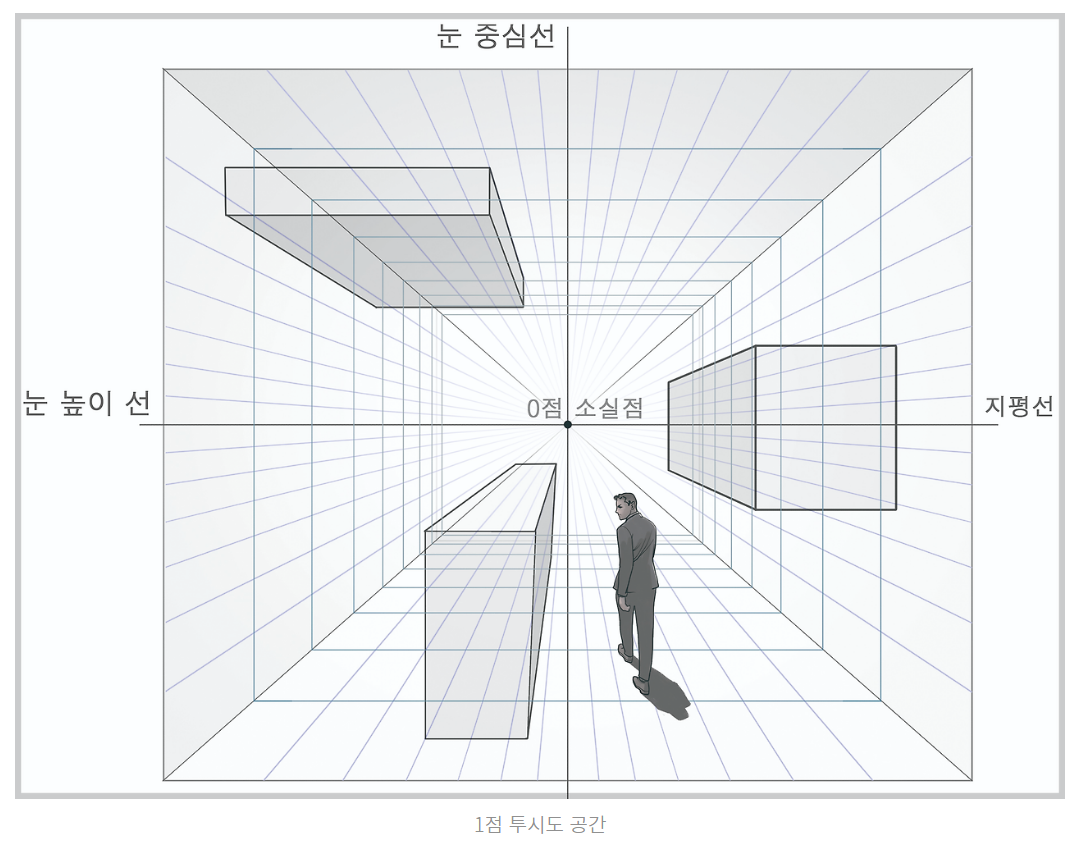
3차원 물체는 관찰자의 위치에서 거리가 멀어질수록 눈에 맺히는 크기가 작아집니다.
이것을 원근이라고 표현합니다.
원근을 구현하는 과정에서 Z값을 처리할 수 있습니다.

이런 식으로 시선 앞의 특정 평면으로 정점들을 투영하면
원근을 구현할 수 있고, Z값을 처리할 수 있습니다.

이런 식으로 투사체와 눈사이 무한한 거리의 가상의 선이 존재하고,
가상의 선과 눈앞의 특정 평면이 만나는 곳을 참고하여 원근을 구현하는 기법은 15~16세기 미술에서 유행하던 기법이라고 합니다.
이런 식으로 정점을 평면에 투영하여 빠르고 정확하게 원근을 표현할 수 있었다고 합니다.
그러면 원근 투영을 설계해보겠습니다.

먼저 투영할 시스템을 먼저 설계해보겠습니다.
먼저, 상이 맺힐 평면을 먼저 선택해야 합니다.
이를 투영평면 혹은 NDC (Nomalized Device Coordinate) 라고 합니다.
카메라 영역을 x = 0 인 평면에서 살펴보겠습니다.

카메라에는 '화각'이 존재합니다.
그리고 카메라와 NDC 사이의 거리를 '초점거리' 라고 표현합니다.
나중에 NDC 평면을 이용해서 많은 연산을 수행해야하기 때문에 계산이 단순성을 위해 일반적으로 NDC의 크기는 상하좌우 1씩 즉, 상하 [-1, 1] 좌우 [-1, 1] 의 크기를 가지도록 고정합니다.
그렇다면, 초점거리 d 는 화각으로 얻어낼 수 있습니다.

이제 NDC에 어떤 정점 P를 투영해봅니다.

카메라 렌즈 앞에 있는 점을 P(0, y, z) 라고 해보겠습니다.
투영한 점 P'를 구하기 위해서는 삼각형의 비를 사용해서 어떤 y점을 구할 수 있습니다.
앞서 월드를 y축을 기준으로 180' 회전시킨것을 기억할 것입니다.
그러므로 카메라 렌즈 앞에 있는 점의 z값은 무조건 음수입니다.
길이 비를 비교하기 위해서는 양수값 즉, -z 값을 사용해야만 합니다.
그래서 최종적인 NDC 좌표위의 y값과 x값을 구하면 위와 같습니다.

깔끔하게 식이 정리됐습니다.
이를 이용해서 4x4 원근 투영행렬을 설계해봤습니다.
다른 뷰 행렬, 모델링 행렬과 곱하기 위해서 4x4 행렬로 만들었습니다.

그런데, 이 행렬에는 문제점이 있습니다.
d값은 상수인데, z값은 정점마다 다르기 때문에 10000개의 다른 정점이 존재한다면, 10000개의 다른 원근 투영 행렬이 필요합니다.
그래서 차라리 -z 는 나중에 그리기 전에 나눠주도록 시스템을 바꾸겠습니다.

해당 원근 투영 행렬을 사용하면 정점이 NDC 평면으로 완벽하게 투영되지 않습니다.
이런 원근 투영 행렬을 통해서 투영되는 평면을 클립 좌표계라고 합니다.
이를 토대로 카메라를 수정해보겠습니다.

그 다음, 원근 투영 행렬을 얻어내는 함수를 정의해봅시다.


최종 행렬에 원근 투영 행렬을 곱해줍니다.

최종적으로 -Z를 나눠줍시다.
두근두근 한 번 확인해볼까요?

??
뭔가 잘못한걸까요?
정점은 NDC 좌표로 투영되었습니다.
NDC 좌표는 가로세로 [-1, 1]의 영역을 가지고 있으므로
현재 화면 해상도까지 늘려줘야 합니다.
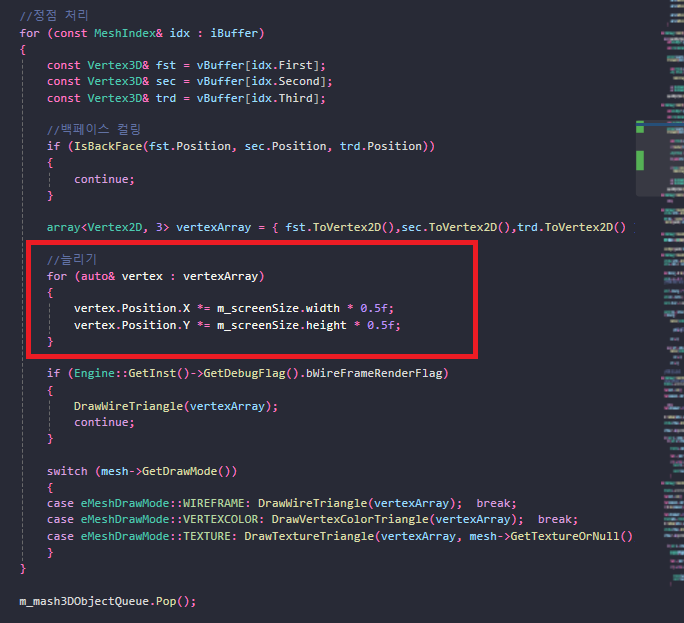
이런 식으로 말이죠
screenSize 에는 현재 화면의 크기가 저장되어 있습니다.
현재 화면의 크기가 800x600 이라고 했을 때, 400, 300을 각각 곱해주면
NDC좌표는 가로 [-400, 400] 세로 [-300, 300]의 영역을 가지게 됩니다.
그렇다면, 다시 실행해봅시다.
대충? 되는 모습을 보이네요!
화각은 다시 설정해야겠지만, 카메라의 원전 (0, 0) 에서 벗어날수록 원점 (소실점) 으로 모이는 듯한 모습을 보입니다.
조금 어색하기는 해두요!
여러 오브젝트를 배치해보겠습니다.
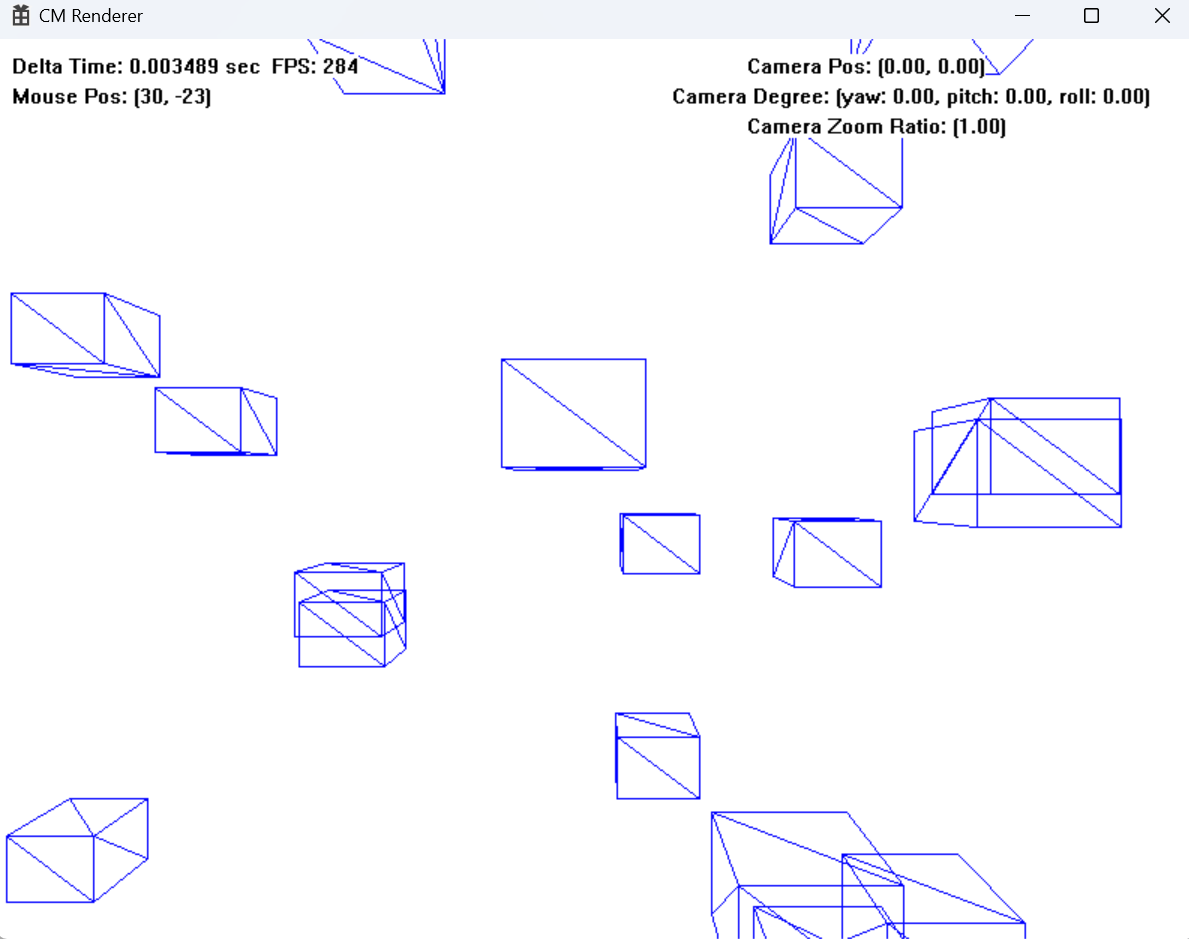
원근감이 느껴지나요?
그런데 이상한게 있습니다.
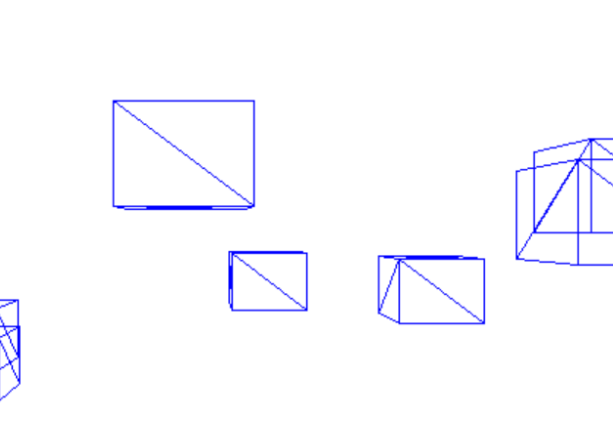
분명 정육면체를 생성했는데,
소실점 주변에 있는 도형들도 정육면체 보다는 직육면체에 가깝습니다.
이는 1:1 NDC 평면을 4:3 윈도우 평면으로 늘렸기 때문입니다.

이를 해결해주기 위해서는 정점 위치를 윈도우 해상도를 고려하여 변형시킬겁니다.
가로와 세로의 비율을 종횡비라고 하는데,
종횡비 a 는 일반적으로 '가로 / 세로' 를 의미합니다.
position.X *= 1/a
를 연산해주면, 정점이 적절하게 변환될 것 같습니다.
연산을 또 해주면, 연산수가 늘어나니 원근 투영행렬에 종횡비 연산을 추가해봅시다.

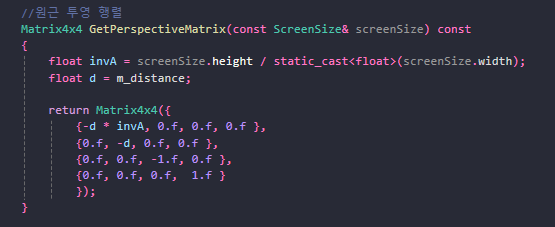
원근 투영 행렬을 수정합니다.
완성된 원근 투영 시뮬레이션을 보겠습니다.
기초적인 텍스처 매핑
매우매우 기본적인 텍스처 매핑을 구현해보겠습니다.
간단하게 UV 좌표, 무게중심좌표 텍스처 매핑을 만들어봤습니다.
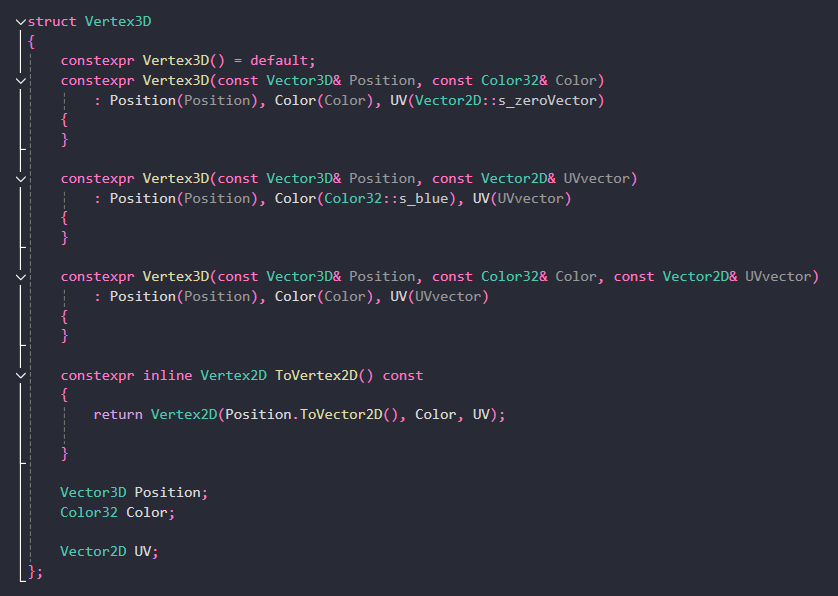
제가 현재 사용하는 정점 Vertex3D 클래스입니다.
Vertex에는 3차원 좌표
색상값, 그리고 텍스처 매핑이 필요할 경우 사용할 UV 좌표계가 존재합니다.
UV좌표계는 U를 가로, V를 세로로하여 [0, 1] 의 범위를 가지는 텍스처 고유의 좌표계입니다.
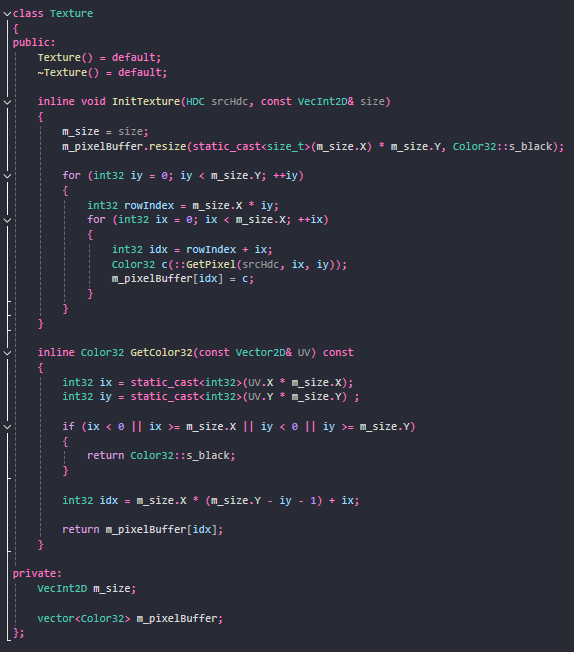
텍스처 클래스에는 이미지의 픽셀 색상 정보를 가지고 있스빈다.
UV 좌표를 넣으면, 해당 텍스처의 픽셀의 색상을 가지고 올 수 있습니다.

정육면체에 씌울만한게 마인크래프트 텍스처가 적당해서, 이 녀석을 한 번 매핑해보도록 하겠습니다.

정점에 적당히 위와같이 UV좌표 정보를 넣어줍시다.
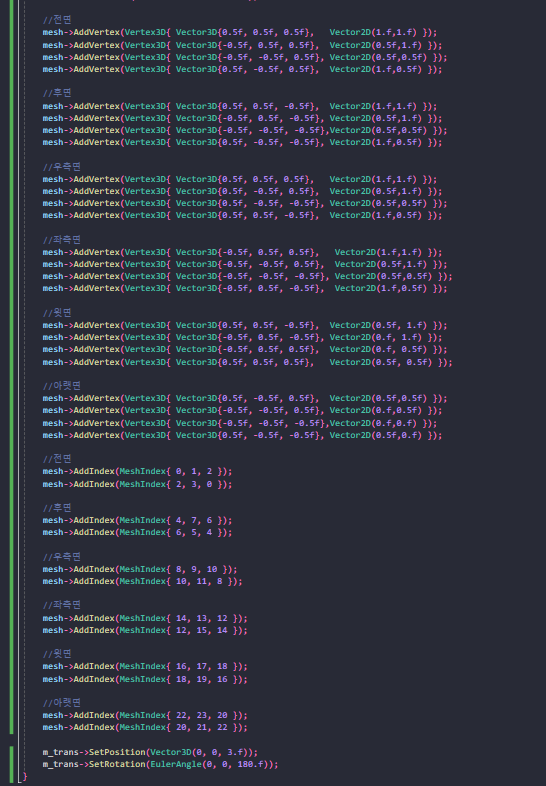
토나올것 같은 정점 정의
컨벡스 결합을 이용해서 삼각형을 그립니다.
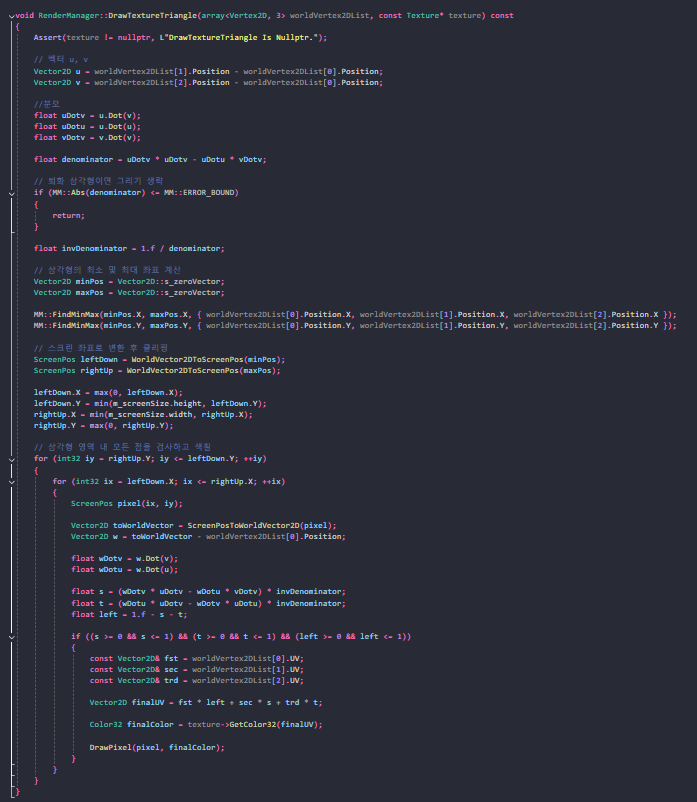
삼각형을 채우는 알고리즘은 다음과 같습니다.
1. 삼각형을 포함하는 가장 작은 사각형영역 찾기
2. 이중 for문 순회하면서, 선택한 점이 삼각형 내부에 위치하는 지 검사
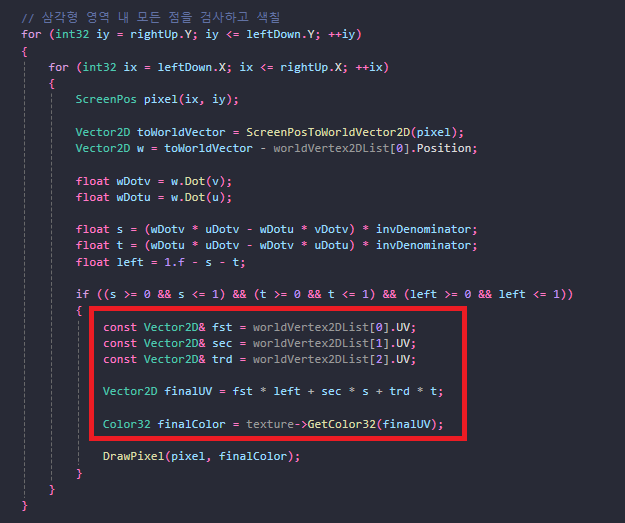
3. 해당 점이 삼각형의 꼭짓점에서 얼만큼 떨어져 있는지 계산 이를 무게중심좌표라고 함
4. 무게중심좌표를 이용해서 UV 좌표 보정
5. UV 좌표로 텍스처에서 픽셀의 색상 얻어옴
6. 점을 찍음
개쩌는 결과를 보겠습니다.

잘 되는것 같습니다.
정점을 조금 잘못설정해서 이미지가 뒤집어지긴 하지만
이는 수정하면 됩니다.
원근 보정 보간
위 영상을 보면 한 가지 문제점이 존재합니다.

뭔가 이런 식으로 찌그러지는 듯한 모습이 거슬립니다.
100% 완벽하게 텍스처매핑이 되지는 않는듯한 모습입니다.
그 이유는 NDC 좌표로 투영된 정점을 가지고 무게중심 보간을 수행했기 때문입니다.
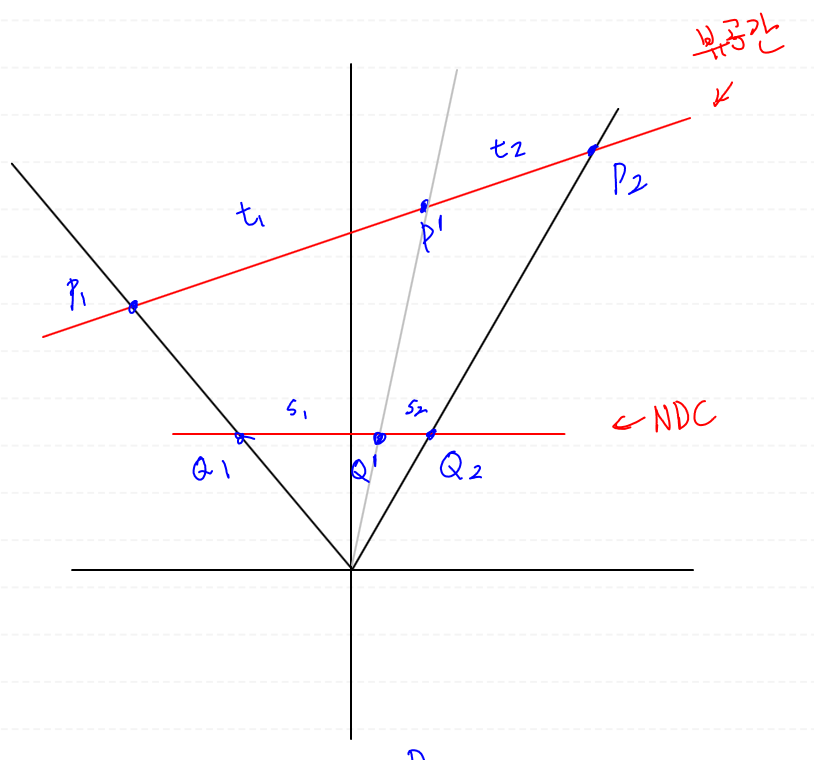
점 P1, P2가 투영되면서 좌표가 변경되었고, 그에따라 무게중심도 바뀌었습니다.
최종적으로 가지고 있는 것은 투영된 정점이 만들어내는 무게중심입니다.
그러나 텍스처는 뷰 공간에 있는 정점을 기준으로 보간되어야 하기 때문에, 제대로 맵핑이 되지 않는 겁니다.
그렇다면, 무게중심 s1, s2를 통해서 투영전 무게중심 t1, t2를 구하면 올바르게 텍스처 매핑을 수행할 수 있을겁니다.

P' 은 P1, P2 직선위에 존재하는 어떤 점
Q'는 Q1, Q1 직선위에 존재하는 어떤 점

점 Q는 P가 투영된 좌표이므로 위와같은 식이 성립

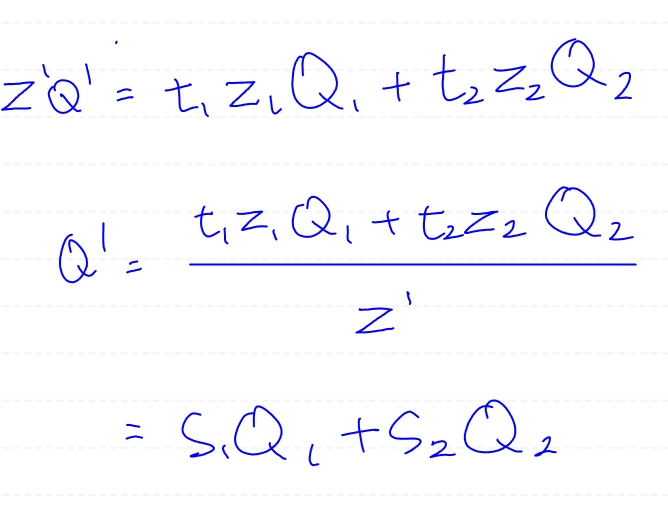
식을 열심히 정리
참고로 해당 식에서 쓰이는 z1, z2은 뷰 공간의 z좌표입니다.
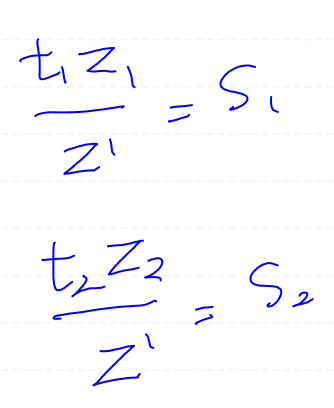
Q의 계수를 비교하면 위와같은 공식을 얻을 수 있습니다.

실제로는 점 2개가 아닌 점 3개로 보간을 수행하기에, 총 3개의 계수를 구해야 합니다.

우리가 구해야하는 것은 t1, t2, t3 이니까, t에 대한 식으로 고쳐줍니다.
우리는 s1, s2, s3는 이미 알고있고, z1, z2, z3는 매개변수로 넘겨주거나, 구조체에 따로 저장하는 방식으로 가져올 수 있습니다.
마지막으로 z' 를 구해봅시다.

컨벡스 결합 식에 의해, 계수의 합은 1입니다.
그러므로 z' 에 대한 식을 얻을 수 있습니다.
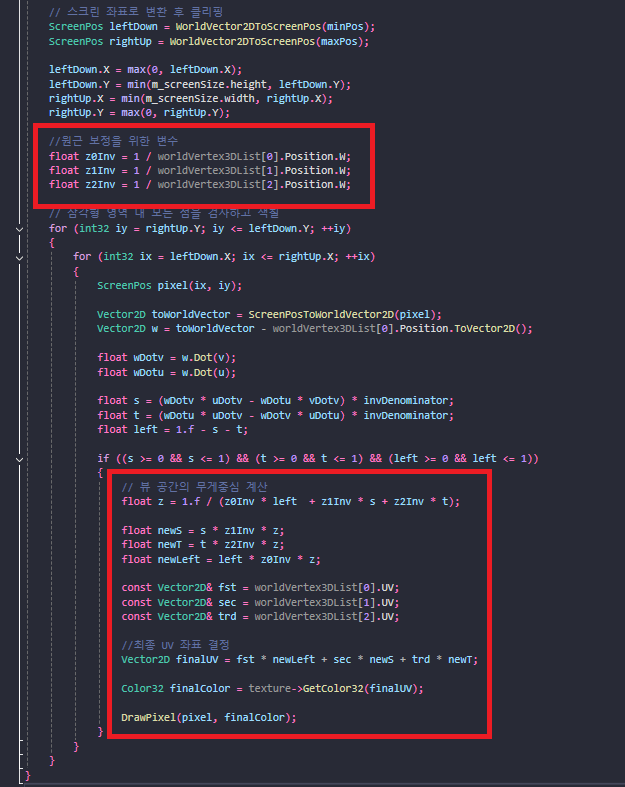
방금 세운 공식을 열심히 적용해줍니다.
결과
생각보다 많이 느리네요...
내일 조금 손봐야겠습니다.
'컴퓨터 그래픽스' 카테고리의 다른 글
| [그래픽스] 가시부피와 절단 (0) | 2024.08.15 |
|---|---|
| [그래픽스] 깊이 구현 (0) | 2024.08.14 |
| [그래픽스] 백 페이스 컬링 (0) | 2024.08.11 |
| [그래픽스] 가볍게 구현해본 3D 와이어 프레임 랜더링 (0) | 2024.08.11 |
| 그래픽스 공부 일지 - 삼각형, 텍스처 매핑 (0) | 2024.08.10 |