참고: https://powerclabman.tistory.com/13
[C++/알고리즘] 퀵 정렬 (Quick Sort)
참고: https://powerclabman.tistory.com/12 [C++/알고리즘] 분할정복 (Divide and Conquer) + 병합정렬 (Merge Sort) 📕 개요 '분할 정복 알고리즘'이란, 엄청나게 크고 방대한 문제를 해결할 수 있는 단위까지 쪼개서
powerclabman.tistory.com
이번 글은 퀵정렬을 모르면 이해하기 힘듭니다.
📕 문제
N 사이즈의 정수배열 arr 이 존재할 때
배열 arr에서 k번 째로 작은 수를 선택해라
예시)
N = 7
arr = {5, 9, 3, 7, 11, 2, 0}
k = 4 일 때, 결과값은 5
설명)
arr을 오름차순 정렬시
0, 2, 3, 5, 7, 9, 11 이므로
4번 째로 작은 수는 5이다.
📘 기본적인 아이디어
빠른 선택이라고 해서 처음에는 '이진 탐색 (Binary Search)'를 사용하려고 했습니다만
이진 탐색은 '정렬된 배열'에서 사용할 수 있기 때문에 적절한 알고리즘이 아니였습니다.
그래서 먼저 빠르게 정렬한 후 k번째 작은 수를 찾으면
효율적이게 숫자를 찾을 수 있지 않을까? 싶어서 고안한 코드는 다음과 같습니다.
#include <iostream>
#define MAX 7
using namespace std;
//퀵소트 관련 함수1
int Partition(int* arr, int start, int end)
{
int pivot = arr[end];
int i = start;
for (int j = start; j < end; j++)
{
if (arr[j] < pivot)
{
swap(arr[j], arr[i]);
i++;
}
}
swap(arr[i], arr[end]);
return i;
}
//퀵소트 관련 함수2
void Qsort(int* arr, int start, int end)
{
if (start < end)
{
int pivot = Partition(arr, start, end);
Qsort(arr, start, pivot - 1);
Qsort(arr, pivot + 1, end);
}
}
int main()
{
int arr[MAX] = {5, 9, 3, 7, 11, 2, 0};
int size = MAX;
int k = 4;
Qsort(arr, 0, size-1);
cout << "찾은 값: " << arr[k-1] << endl;
return 0;
}
위 코드는 그냥 O(n log n) 성능을 보이는 '퀵 정렬'을 한 뒤
k번째 인덱스 값을 출력한 것 입니다.
그렇다면 총 시간 복잡도는 O(n log n) 인 것이죠.
충분히 빠른 알고리즘 입니다.
📗 더 빠르게 찾을 순 없을까?
근데 사실 생각해보면, 굳이 전체 배열을 다 정렬할 필요는 없지 않을까요?
퀵정렬의 파티션 함수를 잘 봅시다.
int Partition(int* arr, int start, int end)
{
int pivot = arr[end];
int i = start;
for (int j = start; j < end; j++)
{
if (arr[j] < pivot)
{
swap(arr[j], arr[i]);
i++;
}
}
swap(arr[i], arr[end]);
return i;
}
피벗을 기준으로
피벗 왼쪽에는 피벗보다 작은 값이
피벗 오른쪽에는 피벗보다 큰 값이 배치됩니다.
그리고 마지막으로 피벗의 인덱스가 리턴되죠.
그러면 리턴 인덱스가 k 값 보다 크다면
왼쪽 파티션에 대해서만 Qsort 함수를 수행하고
그렇지 않다면 오른쪽 파티션에 대해서만 Qsort 함수를 수행하면 더 효율적이지 않을까요?
그리고 리턴 인덱스가 k값과 같다면, 함수가 종료되는 것이죠.
주요한 변경점은 다음과 같습니다.
(파티션 함수는 건들일 필요가 없습니다.)
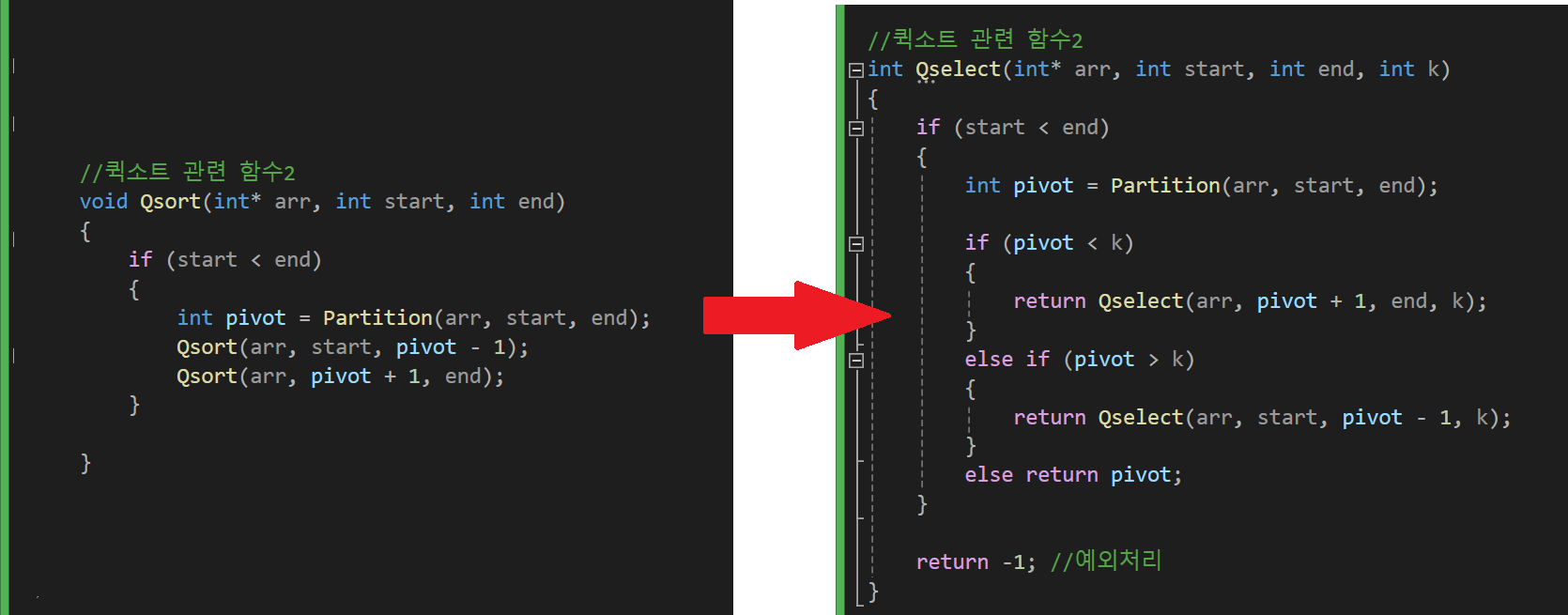
변경된 점은 크게 없습니다.
1. 만약 pivot 값이 k 보다 작다면?
-> 오른쪽 파티션에 대해서 Qselect 재귀 호출
2. 만약 pivot 값이 k 보다 크다면?
-> 왼쪽 파티션에 대해서 Qselect 재귀 호출
3. 만약 pivot 값이 k와 같다면?
-> 찾는 값이므로 return
이 알고리즘은 O(n) 이라는 매우 효율적인 시간 복잡도를 가집니다.
📕코드 완성 및 전체 코드
#include <iostream>
#define MAX 7
using namespace std;
//퀵소트 관련 함수1
int Partition(int* arr, int start, int end)
{
int pivot = arr[end];
int i = start;
for (int j = start; j < end; j++)
{
if (arr[j] < pivot)
{
swap(arr[j], arr[i]);
i++;
}
}
swap(arr[i], arr[end]);
return i;
}
//퀵소트를 이용한 빠른 선택
int Qselect(int* arr, int start, int end, int k)
{
if (start < end)
{
int pivot = Partition(arr, start, end);
if (pivot < k)
{
return Qselect(arr, pivot + 1, end, k);
}
else if (pivot > k)
{
return Qselect(arr, start, pivot - 1, k);
}
else return pivot;
}
return -1; //예외처리
}
int main()
{
int arr[MAX] = {5, 9, 3, 7, 11, 2, 0};
int size = MAX;
int k = 4;
int idx = Qselect(arr, 0, size-1, k-1);
//예외처리
if (idx == -1)
{
cout << "잘못된 요청\n";
exit(0);
}
cout << "찾은 값: " << arr[idx] << endl;
return 0;
}
🎈 마치며
해당 '퀵 셀렉트' 알고리즘은 '로무토 파티션' 알고리즘으로 구현했습니다.
그렇기에 평균적으로 O(n)의 복잡도를 가지지만
최악의 경우 O(n^2) 복잡도를 가질 수 있죠
그런데, '퀵 셀렉트' 자페가 '퀵 정렬'의 알고리즘을 그대로 사용한 것이다보니
'퀵 정렬'의 최적화 아이디어를 그대로 적용할 수 있습니다.
그러면 매우 빠른 시간안에 원하는 수를 찾을 수 있겠죠?
다음에 '퀵 정렬의 최적화 알고리즘'에 대한 포스팅을 하면서 추가적으로 다뤄보기로 하겠습니다.
'알고리즘 > 문제 풀이' 카테고리의 다른 글
| [C++] 백준 11062. 카드 게임 (1) | 2024.02.01 |
|---|---|
| [C++] 백준 13334. 철로 (1) | 2024.01.31 |
| [C++] 백준 1261. 알고스팟 (0) | 2024.01.30 |
| [C++] 백준 17070. 파이프 옮기기1 (1) | 2024.01.30 |
| [C++] 해밍 거리 (Hamming Distance) (0) | 2023.12.24 |